模拟信源的数字化¶

信源编码¶

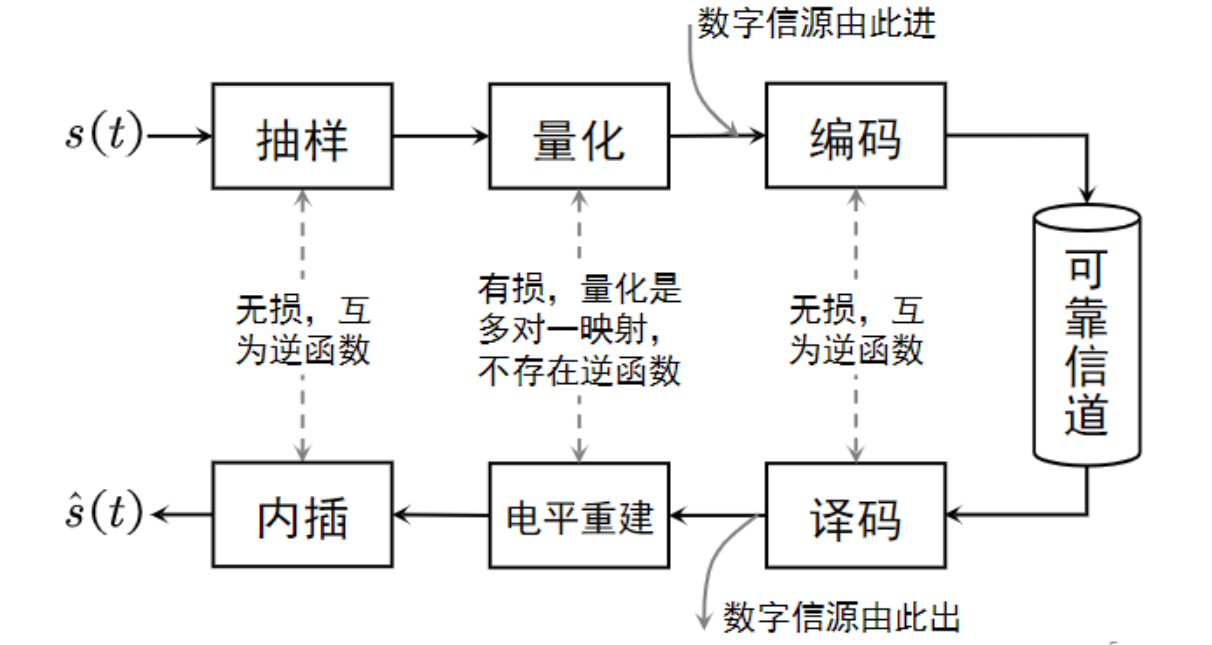
信源编码：将时间连续、幅值连续的模拟信源 \(s(t)\) 映射为 bit 串： \(s(t)\mapsto 01\cdots01\) .

信源编码其需要经过 3 个步骤：

抽样： \(s(t)\to x[k]=s(kT_s)\) ，其中 \(T_s\) 为抽样间隔。由“时间连续，幅值连续”变为“时间离散，赋值连续”。
量化： \(\hat{x}=Q(x)\) ，由“时间离散，幅值连续”变为“时间离散，赋值离散”。
编码： \(\hat{x}\to 01\cdots01\) .

对应到接收端，需要分别进行“译码、电平重建、内插”，从而从 bit 串中恢复处 \(\hat{s}(t)\) .

其中，“抽样/译码”为无损过程，互为反函数。“量化/电平重建”为有损过程，因为量化为多对一映射。“编码/译码”为无损过程，互为反函数。

抽样频率为 \(f_s=\dfrac{1}{T_s}\) ，平均每个抽样量化编码为 \(b\) 个 bit，则信源数字化之后的速率为 \(R=f_s\cdot b \;\text{bit/s}\) .

抽样定理¶

定理描述为：对于带限 \(|f|\leqslant W\) 的低通信号 \(s(t)\) ，当抽样频率 \(f_s\geqslant 2W\) 时可以从抽样信号 \(s(kT_s)\) 中可以无失真地恢复出 \(s(t)\) .

从《信号与系统》的观点出发可以很直观地理解抽样定理：对于每一次抽样，相当于利用冲激信号提取出原始信号在某一时刻的幅度值： \(s(kT_s)=\displaystyle\int_{-\infty}^{+\infty}s(t)\delta(t-kT_s)\mathrm{d}t\) . 这些抽样点组成的序列即为抽样信号 \(\tilde{s}(t)=\displaystyle\sum_k s(kT_s)\delta(t-kT_s)\) ，其傅里叶变换为：

\[ \tilde{S}(f)=\mathcal{F}[\tilde{s}(t)] = \sum_k s(kT_s)\mathcal{F}[\delta(t-kT_s)]=\sum_k s(kT_s)e^{-\mathrm{j}2\pi kfT_s} \]

信号 \(s(t)\) 在时域与冲激串 \(\displaystyle\sum_k\delta(t-kT_s)\) 相乘，等效于在频域频谱 \(S(f)\) 与冲激串卷积，也就是以 \(f_s\) 为周期复制延拓。为了使延拓之后的频谱不发生重叠，应满足 \(f_s\leqslant 2W\) ，即抽样频率必须足够快才能捕获足够的信息进行恢复操作。

最后通过一个带宽也为 \(W\) 的理想低通滤波器，假设其增益为 \(T_s=\dfrac{1}{f_s}\) ，输出的频谱为：

\[ S(f)=\frac{1}{f_s}\sum_k s(kT_s)e^{-\mathrm{j}2\pi kfT_s}\times \mathbb{1}_{|f|\leq W} \]

其中 \(\mathbb{1}_{|f|\leq W}\) 为示性函数，仅在对应区间内值为 \(1\) ，区间外值为 \(0\) . 再进行傅里叶反变换就能提取出原始信号，即时域内插公式：

\[ \begin{align*} s(t) &= \mathcal{F}^{-1}[S(f)] \\ &= \int_{-\infty}^{\infty} S(f) e^{\mathrm{j}2\pi ft} df \\ &= \int_{-W}^{W} \frac{1}{f_s} \sum_k s(kT_s) e^{-j2\pi kfT_s} e^{j2\pi ft} \mathrm{d}f \\ &= \frac{1}{f_s} \sum_k s(kT_s) \int_{-W}^{W} e^{j2\pi f(t-kT_s)} \mathrm{d}f \\ &= \sum_k s(kT_s) \frac{\sin[2\pi W(t-kT_s)]}{\pi f_s (t-kT_s)} \\ &= \sum_k s(kT_s) \frac{\sin[2\pi W(t-k/f_s)]}{\pi (t f_s - k)} \end{align*} \]

可无失真重构 \(s(t)\) 的最小抽样频率 \(f_s = 2W\) 代入时域内插公式得：

\[ s(t) = \sum_k s\left(\frac{k}{2W}\right) \frac{\sin(2\pi Wt - k\pi)}{(2\pi Wt - k\pi)}=\sum_k s\left(\frac{k}{2W}\right) \text{sinc}(2Wt - k) \]

Note

Q：最后为什么使用的是理想低通滤波器，而不是用某一频带范围的理想带通滤波器？抽样信号的频谱经过延拓之后在各个频带内不是完全一致的吗？

A：多数情形下的原始信号（如音频、人声、模拟图像信号等）都是低频带限信号，使用低通滤波器可以直接还原原始信号。高频区域的某一个频带内，频谱确实与零频率附近的频谱形状相同，但是它只是原始信号的一个调制副本，如果不进行解调制，它本身相当于原始信号频谱在频率轴上的偏移，对应于时域用一个复指数信号调制，导致时域信号失真。因此，如果一定要使用带通滤波器的话，必须进行解调制，才能恢复处原始信号。使用低通滤波器的话，不仅物理容易实现，也不需要考虑中心频率（只需要考虑带宽），也省去了解调制的步骤。

对于常见的语音信号，其频率集中在 \(300\sim 3400\text{ Hz}\) ，因此选取的低通滤波器带宽设置为 \(4 \text{ kHz}\) ，抽样频率至少为 \(f_s=2\times 4\text{ kHz}=8\text{ KHz}\) ，每个抽样量化编码为 8 bit，故脉冲抽样调制 PCM 的速率为 \(R=f_sb=8\text{ k}\times 8\text{ bps}=64\text{ kbps}\) .

量化¶

对于连续幅值的变量，理论上需要无穷多个 bit 才能精确表达。实际中我们只能传输有限个 bit，并设定一个能够容忍的误差。

量化：用有限、离散集合中的取值近似表示 \(X\) ，并确保误差尽量小。由于这是一个多对一映射，故不存在逆映射，也是造成失真的根本原因。

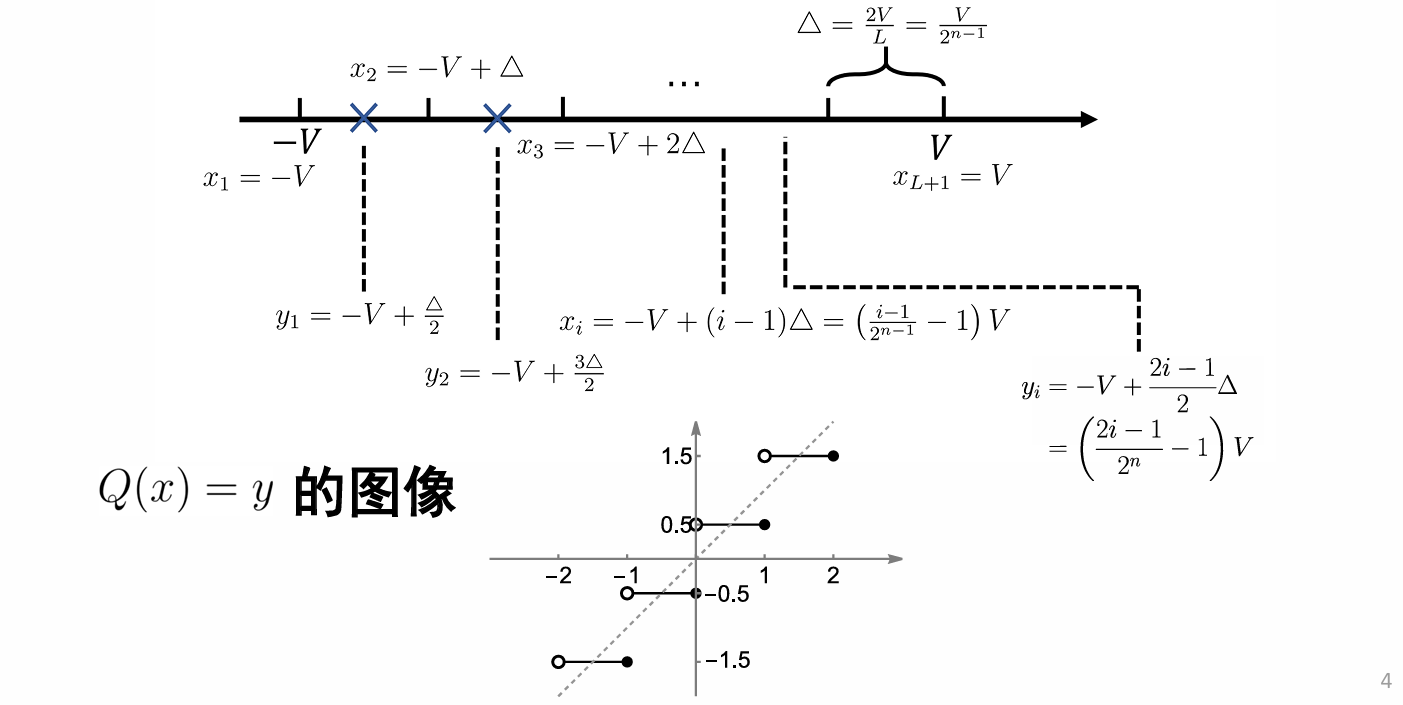
输入 \(x\) 时，重建电平为 \(Q(x)=y_i,\; x_i<x\leqslant x_{i+1}\) . 称 \(x_i\) 为分层电平，是决定重建电平取值的临界值，其最小值和最大值分别为 \(x_{\min}=x_1,\;x_{\max}=x_{L+1}\) .

记： \(I_i=(x_i,x_{i+1}]\) 为第 \(i\) 个量化区间，对应量化间隔为 \(\Delta_i=x_{i+1}-x_i\) . 若 \(\forall i,\Delta_i=\Delta\) 为常数，称为均匀量化，否则为非均匀量化。严格来说，只有 \(X\in[x_{\min},x_{\max}]\) 即量化区间能完全覆盖 \(X\) 的取值时，才算均匀量化。

量化误差 \(e(x)=x=Q(x)\) 为一个随机噪声，均方误差（噪声功率）为：

\[ \sigma^2=\int_{-\infty}^{+\infty}[x-Q(x)]^2p(x)\mathrm{d}x=\sum_{i=1}^L \int_{x_i}^{x_{i+1}}(x-y_i)^2p(x)\mathrm{d}x \]

其中 \(L\) 为重建电平的个数。如果不考虑 \(Q(x)\) 的统计分布，则一个抽样量化需要用 \(\log_2 L\) 个 bit 表示。

噪声功率描述的仅是噪声本身的特性。即使噪声功率较小，如果信号功率本身也较小，那么噪声带来的误差也会较大。功率比较大的信源，一般对量化噪声的容忍程度也比较高，因此定义量化器输出的信噪比：

\[ \mathrm{SNR}_q=\frac{\displaystyle\int_{-\infty}^{+\infty}x^2p(x)\mathrm{d}x}{\displaystyle\sum_{i=1}^L \int_{x_i}^{x_{i+1}}(x-y_i)^2p(x)\mathrm{d}x} \]

如果我们一已知 \(Q(x)\) 的概率分布，就能量身定制一个编码器，使得其输入 \(Q(x)\) 的平均 bit 数最小，也就是熵 \(H(Q(x))\) .

\[ \begin{align*} H(Q(X)) &= -\sum_{i=1}^{L} \mathrm{P}(Q(X) = y_i) \log_2 \mathrm{P}(Q(X) = y_i) \\ &= -\sum_{i=1}^{L} \int_{x_i}^{x_{i+1}} p(x) \mathrm{d}x \log_2 \int_{x_i}^{x_{i+1}} p(x) \mathrm{d}x \end{align*} \]

均匀量化¶

对于幅值有界的变量，在 \([x_{\min},x_{\max}]\) 之间抽样，用 \(n\) 个 bit 进行均匀量化：

幅值区间等分为 \(L=2^n\) 个量化区间 \(I\) .
每个量化区间的长度为 \(\Delta_i=\dfrac{x_{\max}-x_{\min}}{2^n}\) .
每个量化区间的重建电平位于区间中点。
有 \(2^n-1\) 个分层电平均匀分布在区间 \([x_{\min},x_{\max}]\) 内。

一般对称区间容易分析，我们令 \(x_{\min}=-V,x_{\max}=+V,V<+\infty\) ，则：

量化区间间隔 \(\Delta=\dfrac{2V}{L}=\dfrac{V}{2^{n-1}}\) .
重建电平 \(y_i=-V+\dfrac{2i-1}{2}\Delta=\left(\dfrac{2i-1}{2^n}-1\right)V\) .
分层电平 \(x_i=-V+(i-1)\Delta=\left(\dfrac{i-1}{2^{n-1}}-1\right)V\) .

若 \(X\) 均匀分布 \(X\sim\mathcal{U}([-V,V])\) ，则量化噪声为：

\[ \begin{align*} \sigma^2 &= \sum_{i=1}^{L} \int_{x_i}^{x_{i+1}} (x - y_i)^2 \cdot \frac{1}{2V} \cdot \mathrm{d}x \\ &= \frac{L}{2V} \int_{-\Delta/2}^{\Delta/2} x^2 \mathrm{d}x = \frac{1}{\Delta} \cdot \frac{1}{3} \cdot x^3 \bigg|_{-\Delta/2}^{\Delta/2} = \frac{1}{3\Delta} \cdot \left(\frac{\Delta^3}{8} + \frac{\Delta^3}{8}\right) = \frac{\Delta^2}{12} \\ &= \frac{V^2}{2^{2n-2}} \cdot \frac{1}{12} \\ &= \frac{V^2}{3 \times 2^{2n}} \end{align*} \]

信号功率为

\[ P= \int_{-V}^{V} (x)^2 \cdot \frac{1}{2V} \mathrm{d}x = \frac{1}{2V} \cdot \frac{1}{3} \cdot x^3 \bigg|_{-V}^{V} = \frac{V^2}{3} \]

于是：量化信噪比为 \(\mathrm{SNR}_q = \dfrac{P}{\sigma^2} = 2^{2n}\) 。取 dB 为单位，则 \(10 \log_{10} \mathrm{SNR}_q = 20 \log_{10} 2 \times n = 6.02n\) .

结论：编码长度每增加 1 bit，信噪比提升 6.02 dB。

均匀量化对均匀分布是最优的：

重建电平在量化区间中点最优。
分层电平在 \([x_{\min},x_{\max}]\) 中均匀分布最优。

非均匀量化¶

上面讨论的均匀量化有两点启示：

均匀量化对均匀分布是最优的。
量化区间长度 \(\Delta_i\) 越小，该区间内 \(x\) 的（条件）量化噪声越小。

但是抽样的幅值 \(X\) 一般不满足均匀分布，因此我们需要寻找与 \(X\) 分布尽量匹配的量化器，且希望概率密度 \(p_X(x)\) 较大的地方，量化区间长度尽量小，量化更精细一些。类比城市轨道交通，人口密度越大的地方需要设置更密集的站点。

定量分析：在给定量化区间个数 \(L\) 的情况下，量化噪声为 \(\sigma^2=\displaystyle\sum_{i=1}^L \int_{x_i}^{x_{i+1}}(x-y_i)^2p(x)\mathrm{d}x\) ，求偏导寻找极值：

\[ \begin{align*} \frac{\partial \sigma^2}{\partial x_i} &= 0 \iff x_i = \frac{y_{i-1} + y_i}{2} \\ \frac{\partial \sigma^2}{\partial y_i} &= 0 \iff y_i = \frac{\displaystyle\int_{x_i}^{x_{i+1}} x p(x) \mathrm{d}x}{\displaystyle\int_{x_i}^{x_{i+1}} p(x) \mathrm{d}x} \end{align*} \]

（1）分层电平 \(x_i = \dfrac{y_{i-1} + y_i}{2}\) ，称为最近邻居准则。直观理解：地铁站点为重建电平，距离那个站近去哪个，而“远近”的分界点一定在两个地铁站的正中间。

应用：

给定重建电平，求分层电平。
给定译码器输出电平集合，优化编码器。这两个计算均与变量的分布 \(p_X(x)\) 无关。

（2）重建电平 \(y_i = \dfrac{\displaystyle\int_{x_i}^{x_{i+1}} x p(x) \mathrm{d}x}{\displaystyle\int_{x_i}^{x_{i+1}} p(x) \mathrm{d}x}\) ，称为重心准则。在一个量化区间 \((x_i,x_{i+1}]\) 内，重建电平 \(y_i\) 应该更偏向概率密度更大的一方。直观理解：地铁站应该建在人口密度最大的地方。

应用：

给定 \(X\) 的分布和分层电平，求重建电平。
给定信源统计特性和编码器，优化译码器的输出电平集合。这两个计算均与变量的分布 \(p_X(x)\) 有关。

量化器的过载¶

显然，量化器 \(Q(x)\) 的性能与信源 \(X\) 的分布 \(p(x)\) 密切相关。不存在普适最优的量化器，实际中量化器都是给定的。过载，就是一种典型的量化器与信源分布失配的情况。即量化器设计只考虑了 \([-V, V]\) 之间的 \(X\)，当输入超出了量化器设计的量化范围，即 \(x>V\) 或 \(x<-V\) 时，就会发生过载。

发生过载的概率：

\[ \left( \int_{-\infty}^{-V} + \int_{V}^{+\infty} \right) p(x) \mathrm{d}x \]

过载噪声：

\[ \begin{align*} \sigma_o^2 &= \int_{-\infty}^{-V} (x - y_1)^2 p(x) \mathrm{d}x + \int_{V}^{+\infty} (x - y_L)^2 p(x) \mathrm{d}x \qquad (\Delta_1,\Delta_L\ll V)\\ &= \int_{-\infty}^{-V} (x + V)^2 p(x) \mathrm{d}x + \int_{V}^{+\infty} (x - V)^2 p(x) \mathrm{d}x \end{align*} \]

正常量化噪声：\(\sigma_q^2 = \displaystyle\int_{-V}^{V} (x - Q(x))^2 p(x) \mathrm{d}x\)

有过载时的总量化噪声 \(\sigma^2 = \sigma_q^2 + \sigma_o^2\) .

从非均匀量化角度看过载：

最左端量化区间 \(I_1\) 从 \([-V,x_2]\) 扩展为 \((-\infty,x_2]\) .
最右端量化区间 \(I_L\) 从 \((x_L,V]\) 扩展为 \((x_L,+\infty]\) .
两端的分层电平 \(y_1,y_L\) 可以不变，也可以进一步优化。
对于 \((-\infty,+\infty)\) 上的分布，只有非均匀量化可以无过载，均匀量化一定有过载。因为均匀量化必须在有限长度区间上进行，例如高斯分布的变量，就无法使用均匀量化。

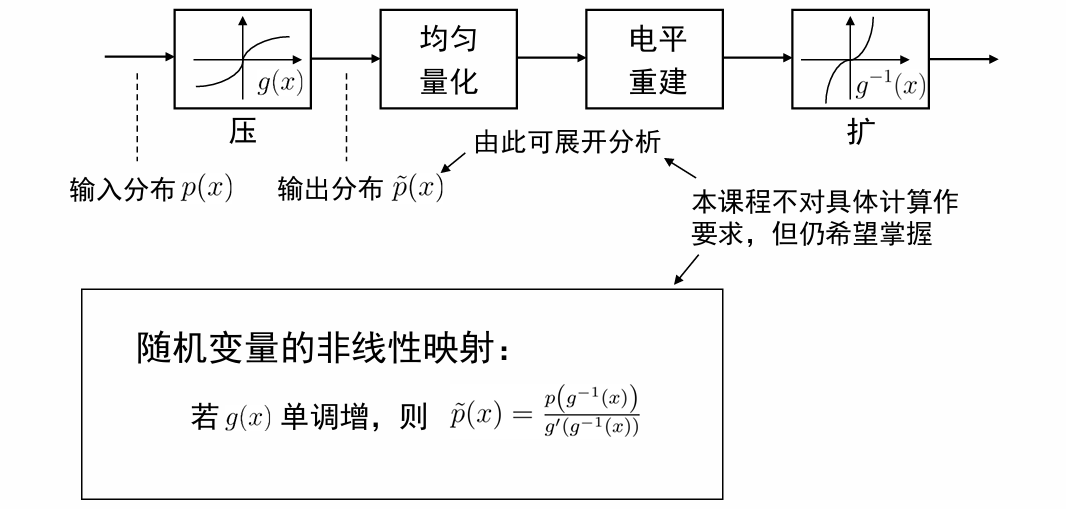
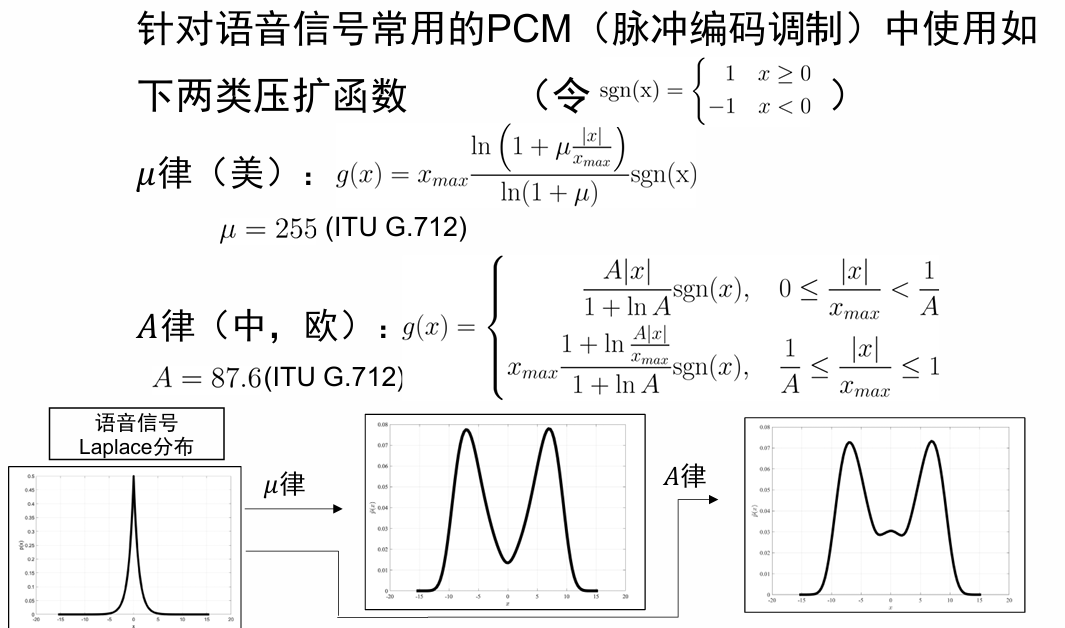
压扩原理¶

动机与出发点：

反正不存在普适的最优量化器。
非均匀量化的设计，优化和执行复杂。
均匀量化的分析和实现都更容易。
均匀量化与均匀分布适配的更好。

注意到：非线性映射可以改变随机变量的分布形状。因此，我们希望通过可逆映射，让 \(p(x)\) 变的更接近于均匀分布。

压扩系统：接收端用非线性映射 \(g(x)\) 的逆映射 \(g^{-1}(x)\) 从重建电平中进一步恢复原始信号。

高分辨率量化¶

当量化 bit 数 \(n\) 较大，区间数 \(L\) 大到让任意量化区间 \(I_i = (x_i, x_{i+1}]\) 中 \(p(x)\) 近似均匀时，即：

\[ p(x) \approx \frac{\displaystyle\int_{x_i}^{x_{i+1}} p(x) dx}{\Delta_i}, \quad x \in I_i \]

记 \(P_i = \displaystyle\int_{x_i}^{x_{i+1}} p(x) dx\) ，则：

\[ \begin{align*} \sigma^2 &= \sum_{i=1}^{L} \int_{x_i}^{x_{i+1}} (x - y_i)^2 \frac{P_i}{\Delta_i} \mathrm{d}x \\ &= \sum_{i=1}^{L} \frac{P_i}{\Delta_i} \int_{x_i}^{x_{i+1}} (x - y_i)^2 \mathrm{d}x \end{align*} \]

由 \(I_i\) 中的均匀分布近似知， \(y_i^* = \dfrac{x_i + x_{i+1}}{2}\) ，类比均匀量化中的分析：

\[ \sigma^2 = \sum_{i=1}^{L} \frac{P_i}{\Delta_i} \frac{\Delta_i^3}{12} = \frac{1}{12} \sum_{i=1}^{L} P_i \Delta_i^2 \]

若量化间隔都相等 \(\Delta_i \equiv \Delta, \forall i\) ，则量化噪声为 \(\sigma^2 = \dfrac{\Delta^2}{12} \displaystyle\sum_{i=1}^{L} P_i = \dfrac{\Delta^2}{12}\) .

若对高分辨率量化后的结果做无损压缩，则：

\[ \begin{align*} H(Q(X)) &= -\sum_i P_i \log P_i \\ &\approx -\sum_i p(x_i) \Delta_i \log p(x_i) \Delta_i \\ &= -\sum_i p(x_i) \log p(x_i) \Delta_i - \sum_i p(x_i) \Delta_i \log \Delta_i \\ &= -\int p(x) \log p(x) \mathrm{d}x + \log \frac{1}{\Delta} \qquad (\sigma^2=\frac{\Delta^2}{12}\Rightarrow \Delta=2\sqrt{3}\sigma)\\ &= h(X) + \log \frac{1}{2\sqrt{3}\sigma} \\ &= h(X) - \log \sigma - 1.8 \end{align*} \]