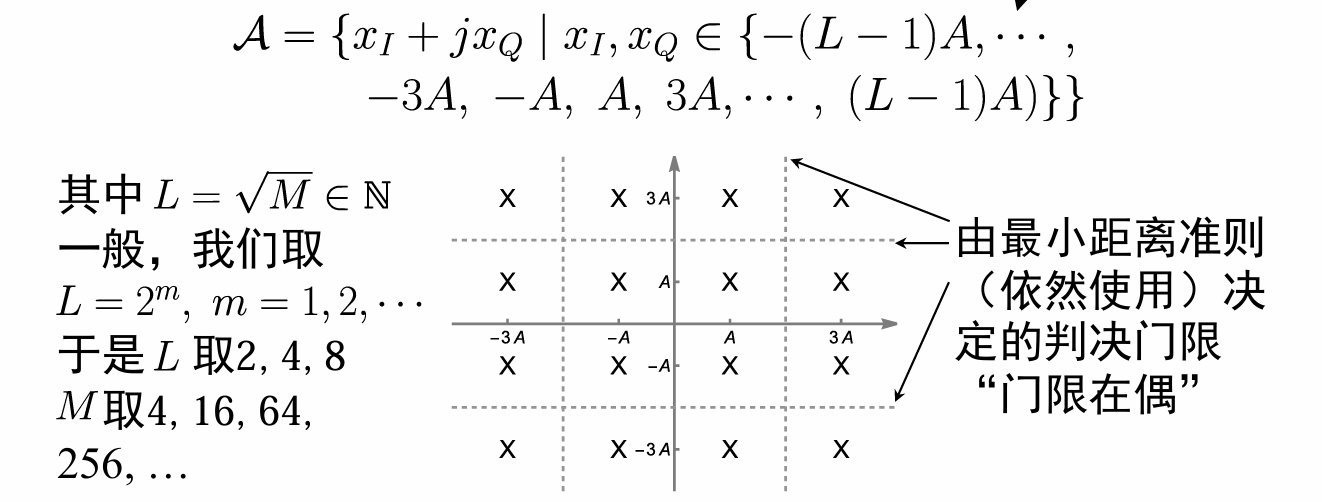Skip to content

电平信道

Abstract

重点掌握： 1. 最佳判决准则及其应用。 2. 计算判决门限和差错概率。 3. 多进制传输中的每符号比特承载量计算，比特与符号能量的互算。 4. 多进制实电平和复电平传输的差错概率计算。

在之前的讨论中，我们将信源编码为 0,1 bit，其中 0,1 bit 是逻辑量，而我们需要在实际的物理信道中使用物理量传输 0,1 bit。实际信道存在各种失真，例如噪声、带宽限制。我们追求在使用尽量少的资源（功率，带宽）的条件下获得较高的通信速率和较好的可靠性。

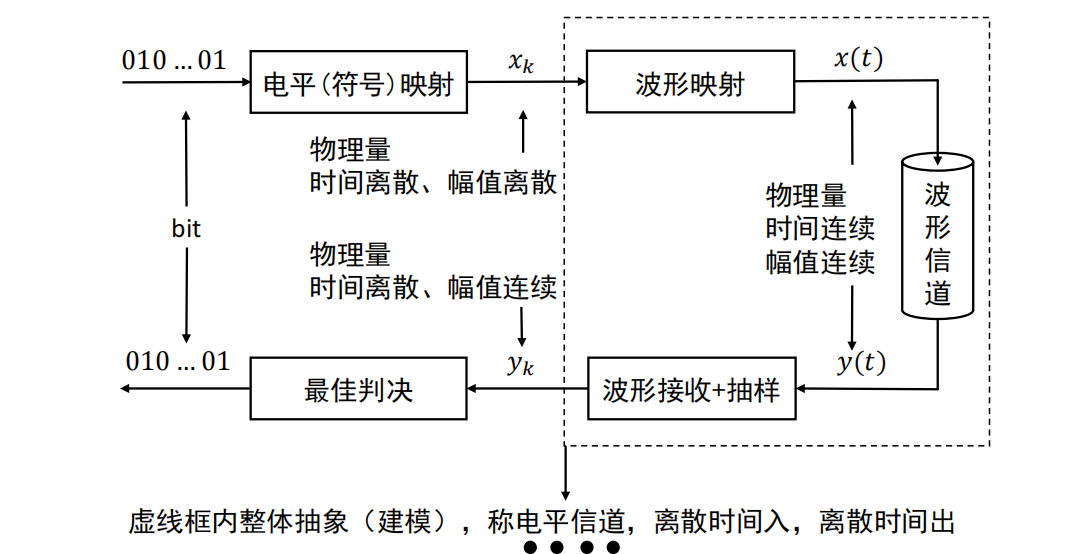
数字调制的基本结构：

202508051036272

类似互信息部分的讨论，我们使用条件概率 \(p(y\mid x)\) 建模一个信道，在输入为 \(x\) 的情况下观测 \(y\) 值出现的概率：

\[ x_k \longrightarrow \boxed{p(y\mid x)} \longrightarrow y_k \]

且有：

  1. 信道无记忆，否则条件概率应写为 \(p(y_1,\cdots,y_k,\cdots\mid x_1,\cdots,x_k,\cdots)\) .
  2. \(x_k\) 独立同分布，故 \(y_k\) 独立同分布。在之后的讨论中可以忽略下标 \(k\) .
  3. \(x\) 从离散集合中取值，但考虑到噪声， \(y\in\mathbb{R}\) 一般取实数。

我们考虑加性高斯白噪声电平信道：

\[ \begin{matrix} & z\overset{i.i.d}{\sim} \mathcal{N}(0,\sigma^2) & \\ & \downarrow & \\ x \longrightarrow & \oplus & \longrightarrow y=x+z \end{matrix} \]

其中噪声 \(z\) 为独立同分布的高斯随机变量。

二进制传输

仅传输一个 bit：0 或 1。

  1. 若传输 “0”，则发送电平 \(-A\) .
  2. 若传输 “1”，则发送电平 \(+A\) .

上述称为“电平映射”或“符号映射”。实现了从逻辑量（bit）到物理量（电平）的转换。

假设信源编码的输出比特 0,1 等概分布（事实上，最优信源编码就满足这一点），则 \(p(A)=p(-A)=\dfrac{1}{2}\) .

\[ \begin{matrix} & z & \\ & \downarrow & \\ x\in\{-A,A\} \longrightarrow & \oplus & \longrightarrow y=\pm A+z \end{matrix} \]

接收电平 \(y\) 的条件分布为 \(y\mid x\sim\mathcal{N}(x,\sigma^2)\) ，即：

\[ p(y\mid A) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(y-A)^2}{2\sigma^2}},\quad p(y\mid -A) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(y+A)^2}{2\sigma^2}} \]

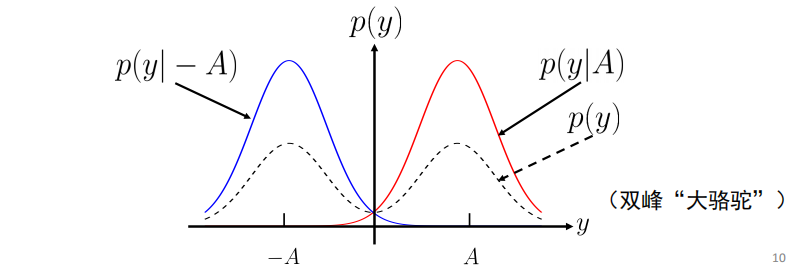
根据全概率公式：

\[ \begin{align*} p(y) &= p(A) p(y\mid A) + p(-A) p(y\mid -A) \\ &= \frac{1}{2\sqrt{2\pi\sigma^2}} \left( e^{-\frac{(y-A)^2}{2\sigma^2}} + e^{-\frac{(y+A)^2}{2\sigma^2}} \right) \end{align*} \]

202508051056649

无论发送的是 \(A\) 还是 \(-A\) ， \(y\) 都分布于整个实轴。因此对于接收到的任意 \(y\) ，极有可能是发送 \(A\) 导致的，也有可能是发送 \(-A\) 导致的，我们无法绝对准确地判断发送电平到底是哪一个。因此我们需要寻找一种判决准则，对接收电平强行判决其发送电平，并使得判决尽可能准确。

根据贝叶斯决策理论，我们执果索因。 \(y\) 是已知的，是观测值， \(x\) 是未知的，是随机变量。条件于观测值 \(y\) ，根据最大后验概率准则 MAP：

  1. 出现 \(A\) 的条件概率更大，即 \(\Pr(x=A\mid y)>\Pr(x=-A\mid y)\) ，则判决为 \(\hat{x}=A\) .
  2. 出现 \(-A\) 的条件概率更大，即 \(\Pr(x=A\mid y)<\Pr(x=-A\mid y)\) ，则判决为 \(\hat{x}=-A\) .
\[ \frac{p(y\mid A)p(A)}{p(y)} \overset{\hat{x}=A}{\underset{\hat{x}=-A}{\gtrless}}\frac{p(y\mid -A)p(-A)}{p(y)} \iff p(y\mid A) \overset{\hat{x}=A}{\underset{\hat{x}=-A}{\gtrless}} p(y\mid -A) \]

即为最大似然准则。带入得到：

  1. \(y>0,\quad p(y\mid A)>p(y\mid -A)\) ，判决为 \(\hat{x}=A\) .
  2. \(y<0,\quad p(y\mid A)<p(y\mid -A)\) ，判决为 \(\hat{x}=-A\) .

\(y=0\) 为最佳判决门限，也很容易直观理解。发送电平关于 0 对称，噪声也为零均值，根据对称性，判决门限在正中间最合理。

误符号率（差错概率）：判决输出电平（符号）不等于发送电平（符号）的概率 \(P_s=\Pr(\hat{x}\neq x)\) .

对于二进制传输：

\[ \begin{align*} P_s&=p(A)p(y<0\mid A)+p(-A)p(y>0\mid -A) \\ &=\frac{1}{2}p(y<0\mid A)+\frac{1}{2}p(y>0\mid -A) \\ &=\frac{1}{2}Q\left(\frac{A}{\sigma}\right)+\frac{1}{2}Q\left(\frac{A}{\sigma}\right) \\ &=Q\left(\frac{A}{\sigma}\right) \end{align*} \]

其中 \(Q(u)=\displaystyle\int_u^{+\infty}\dfrac{1}{\sqrt{2\pi}}e^{-t^2/2}\mathrm{d}t\) 是标准高斯分布的截尾误差函数。可以理解为高斯分布的“反向累积分布函数”，且是一个减函数： \(Q(-\infty)\to1,\;Q(0)=\dfrac{1}{2},\;Q(+\infty)\to 0\) .

可见，差错概率仅与发送电平到判决门限的距离、噪声方差有关。

电平信道的每符号能量 \(E_s=\mathbb{E}(x^2)\) .

对于二进制传输， \(E_s=\dfrac{1}{2}A^2+\dfrac{1}{2}(-A)^2=A^2,\;A=\sqrt{E_s}\) .

而电平信道的信噪比 \(\mathrm{SNR}=\dfrac{E_s}{\sigma^2}\) ，故误符号率 \(P_s=Q\left(\dfrac{A}{\sigma}\right)=Q\left(\sqrt{\dfrac{E_s}{\sigma^2}}\right)=Q\left(\sqrt{\mathrm{SNR}}\right)\) .

电平信道中一个符号可能由多个 bit 共同表示。因此我们还需要考虑误比特率。

对于二进制传输，一个符号就是一个 bit，因此：

\[ P_b=P_s,\quad E_b=E_s \]

多进制实电平传输

二进制传输中，一个电平只能承载 1 个 bit。如果扩大电平 \(x\) 的取值集合，也就是增大信源的熵，那么一个电平就可以承载多个 bit，承载的信息量更大。

\(M\) 进制传输：给定电平集合 \(\mathcal{A}\) ，其势为 \(|\mathcal{A}|=M\) ，一个电平最多可以承载 \(n=\left\lfloor \log_2M \right\rfloor\) 个 bit。

通常我们取 \(M\) 为 2 的整数次幂，即 \(M=2^n,\;n\in\mathbb{N}\) .

\(M\) 进制实电平传输：

\[ \begin{matrix} & z & \\ & \downarrow & \\ x\in\mathcal{A} \longrightarrow & \oplus & \longrightarrow y=x+z \in \mathbb{R} \end{matrix} \]

通常取电平集合对称分布

\[ \mathcal{A}=\{-(M-1)A,-(M-3)A,\cdots,-3A,-A,A,3A,\cdots (M-1)A,(M-3)A\} \]

电平和 bit 的映射满足格雷映射，相邻电平对应的 bit 串，只有一位 bit 不同。目的是减小误 bit 率。

\[ \begin{align*} M=4 &\quad \{00,01,11,10\} \\ M=8 &\quad \{000,001,011,111,101,100,110,010\} \end{align*} \]

类似二进制传输的讨论，无论发哪个电平 \(x\) ，接收电平 \(y\) 都可能出现在实轴上任意一点。判决准则为 \(\hat{x}=\displaystyle\arg\max_{x\in\mathcal{A}}p(x\mid y)\) .

\[ \begin{align*} \hat{x} &= \arg\max_{x \in \mathcal{A}} p(x\mid y) \\ &= \arg\max_{x \in \mathcal{A}} \frac{p(y\mid x)p(x)}{p(y)} \\ &= \arg\max_{x \in \mathcal{A}} p(y\mid x)p(x) \\ &= \arg\max_{x \in \mathcal{A}} p(y\mid x) \\ &= \arg\max_{x \in \mathcal{A}} \frac{1}{\sqrt{2\pi\sigma^2}} \exp \left( -\frac{(y - x)^2}{2\sigma^2} \right) \\ &= \arg\min_{x \in \mathcal{A}} (y - x)^2 \\ &= \arg\min_{x \in \mathcal{A}} |y - x| \end{align*} \]

最小距离准则：\(\hat{x}=\displaystyle\arg\min_{x \in \mathcal{A}} |y - x|\) ，接收到的 \(y\) 距离 \(\mathcal{A}\) 中哪个 \(x\) 近，就判决为哪个 \(x\) .

判决门限集合为 \(\{-(M-2)A,\cdots,-2A,0,2A,\cdots,(M-2)A\}\) .

与二进制传输不同，多进制传输由于有多个判决门限，发生差错时可能向左右两个方向差错。由于判决门限到电平的距离仍为 \(A\) ，因此单边差错概率为 \(Q\left(\dfrac{A}{\sigma}\right)\) ，双边差错概率为 \(2Q\left(\dfrac{A}{\sigma}\right)\) .

中间 \((M-2)\) 个点会发生双边差错，最外侧的 \(2\) 个点只会发生单边差错，因此误符号率为：

\[ \begin{align*} P_s&=\frac{2}{M}\cdot Q\left(\dfrac{A}{\sigma}\right)+\frac{M-2}{M}\cdot 2Q\left(\dfrac{A}{\sigma}\right) \\ &=\frac{2M-2}{M}Q\left(\dfrac{A}{\sigma}\right) \end{align*} \]

信号功率为 \(E_s=\mathbb{E}(x^2)=\dfrac{1}{M}\cdot2[A^2+(3A)^2+\cdots((M-1)A)^2]=\dfrac{A^2(M^2-1)}{3}\) .

单个 bit 能量 \(E_b=\dfrac{E_s}{\log_2M}\) .

替换掉 \(A\) 得到：

\[ P_s=\frac{2M-2}{M}Q\left(\sqrt{\frac{3}{M^2-1}\cdot \frac{E_s}{\sigma^2}}\right) \]

由此也可见，信噪比 SNR 越大，差错概率越小。

对于格雷映射的编码：相邻符号对应的 bit 串只有一位不同，错到相邻电平时只会导致 1 个 bit 差错，而在信噪比较高时，噪声使得电平差错到非相邻电平的概率很小，可以忽略。因此得到误 bit 率 \(P_b\approx\dfrac{P_s}{\log_2M}\) . 注意这里是约等于号，因为我们忽略了差错到非相邻电平的极小概率事件。

Tip

记忆口诀：一个电平符号对应 \(\log_2M \geqslant 1\) 个 bit，因此每 bit 能量小于每符号能量 \(E_b\leqslant E_s\) . 传输一个电平符号的 \(\log_2M\) 个 bit，即使符号判决错误，也仅仅差错了 1 个 bit，因此 \(P_b<P_s\) .

复电平信道

加性复高斯白噪声信道：

\[ \begin{matrix} & z\sim\mathcal{CN}(0,2\sigma^2) & \\ & \downarrow & \\ x=x_I+\mathrm{j}x_Q \longrightarrow & \oplus & \longrightarrow y=x+z=(x_I+z_I)+\mathrm{j}(x_Q+z_Q) \end{matrix} \]

复高斯噪声 \(z\sim\mathcal{CN}(0,2\sigma^2)\) ，实部虚部为独立同分布的零均值高斯随机变量，其概率分布为：

\[ p(z_I,z_Q)=p(z_I)p(z_Q)=\dfrac{1}{2\pi\sigma^2}e^{-(z_I^2+z_Q^2)/2\sigma^2} \]

如果输入电平 \(x=x_I+\mathrm{j}x_Q\) 的 I,Q 两路（实部和虚部）正交独立，那么接收端的 \(y=x+z=(x_I+z_I)+\mathrm{j}(x_Q+z_Q)\) 的 I,Q 两路也完全独立。

Note

这里的复数只是我们进行等效数学建模的手段，现实生活中不存在复数的物理量。

典型复电平集合 1：正方形格点，星座图。

\[ \mathcal{A}=\{x_I+\mathrm{j}x_Q|x_i,x_Q\in\{-(L-1)A,\cdots,-A,A,\cdots,(L-1)A\}\} \]

202508091511533

对于 \(M\) 进制复电平传输，一共 \(M\) 个点，每一路有 \(L=\sqrt{M}\in\mathbb{N}\) 列。因此 \(M\) 的取值一般为 4 的整数次幂（因为要保证是完全平方数） \(4,16,64,\cdots\) .

根据 I,Q 两路的独立性，复电平传输可等价为两路独立的 \(L=\sqrt{M}\) 进制实电平传输。

分析差错概率时，接收端 \(y\) 必须实部和虚部都判别正确，才算复电平 \(x\) 判决正确，因此误符号率为两路电平误符号率的逻辑并集：

\[ \begin{align*} P_s&=1-\Pr(\hat{x}_I=x_I)\times \Pr(\hat{x}_Q=x_Q) \\ &=1-(1-P_s^I)(1-P_s^Q) \\ &=P_s^I+P_s^Q-P_s^IP_s^Q \end{align*} \]

根据多进制实电平传输，其中 \(P_s^I=P_s^Q=\dfrac{2(\sqrt{M}-1)}{\sqrt{M}}Q\left(\dfrac{A}{\sigma}\right)\) ，且信噪比较高时 \(P_s^IP_s^Q\) 作为二阶小量可以忽略。因此：

\[ P_s \approx P_s^I+P_s^Q=4\left(1-\frac{1}{\sqrt{M}}\right)Q\left(\dfrac{A}{\sigma}\right),\quad P_b\approx\frac{P_s}{\log_2M} \]

一个复电平信号的能量等价于两路实电平能量的和（因为正交）：

\[ E_s=\mathrm{E}(|x|^2)=2\times \frac{(\sqrt{M})^2-1}{3}A^2=\frac{2(M-1)}{3}A^2 ,\quad E_b=\frac{E_s}{\log_2M} \]

注意这里对数中的是 \(M\) 而不是 \(\sqrt{M}\) .

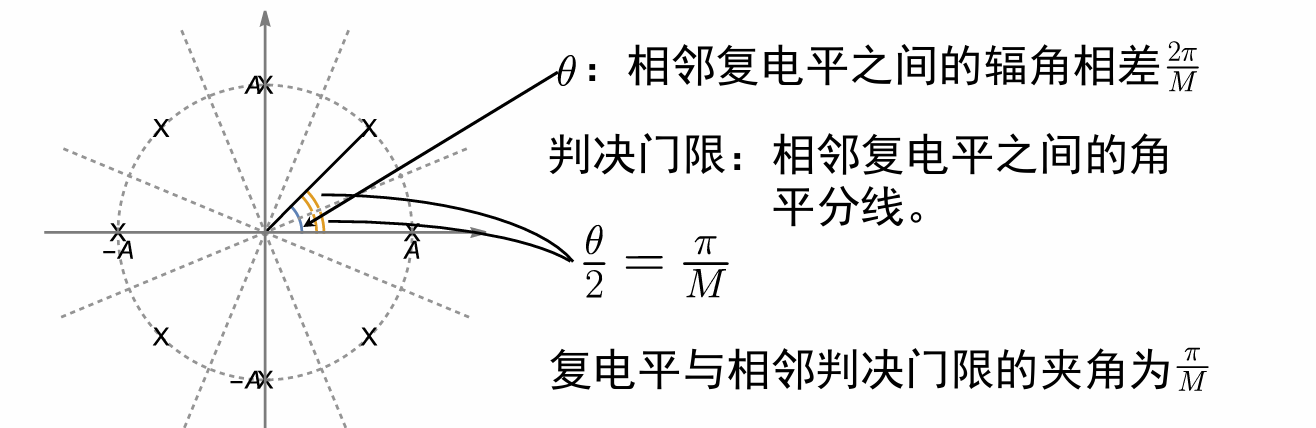
典型复电平集合2：圆上均匀分布的点。

\[ \mathcal{A}=\left\{A,Ae^{\mathrm{j}\theta},Ae^{\mathrm{j}2\theta},\cdots, Ae^{\mathrm{j}(M-1)\theta}\right\},\quad \theta=\frac{2\pi}{M} \]

202508091512321

所有电平模长相等，辐角相差 \(\dfrac{2\pi}{M}\) ，判决门限为相邻电平的角平分线，故复电平和判决门限的夹角为 \(\dfrac{\pi}{M}\) .

\[ E_s=\mathbb{E}(|x|^2)=A^2, \quad E_b=\frac{E_s}{M} \]

分析差错概率时，由于循环对称性，只需要考虑任意一个电平（与实电平传输不同是因为边界电平和内部电平不等价），例如最容易分析的 \(x=A\) 电平：

\[ P_s=\Pr(\hat{x}\neq A\mid x=A)=\Pr(|\angle(A+z)|>\frac{\pi}{M}\mid x=A) \]

直接积分较为困难，而一般 \(M,\dfrac{A}{\sigma}\) 较大时，电平 \(A\) 看到的 2 个判决门限 \(e^{\mathrm{j}\pi/M},e^{-\mathrm{j}\pi/M}\) 夹角较小，近似平行，只有 \(z_Q\) 会引起差错：

\[ P_s=\Pr(|z_Q|>d)=2Q\left(\frac{d}{\sigma}\right),\quad d=A\sin\frac{\pi}{M}=\sqrt{E_s}\sin\frac{\pi}{M} \]

得到：

\[ P_s=2Q\left(\frac{A}{\sigma}\sin\frac{\pi}{M}\right),\quad P_b=\frac{P_s}{\log_2 M} \]

当 \(M\) 较大时，可近似 \(\sin\dfrac{\pi}{M}\approx \dfrac{\pi}{M}\) .

Comments