波形信道¶

Abstract

重点掌握： 1. 波形传输中符号能量的计算。 2. 对噪声作线性处理（滤波）后的数字特征（主要是方差）计算。 3. 对接收波形被线性处理的形式，应用和输出信噪比计算。 4. 匹配滤波的形式、应用、输出信噪比计算和标准等效电平信道的传输形式。 5. 抽样点无失真的初步概念。 6. 满足抽样点无失真时，收发联合等效系统的频响 \(H(f)\) 的特征，由此推算符号速率 \(R_s\) 的上限，和 \(H(f)\) 的带宽 \(W\) 的下限。 7. 矩形包络载波传输的收发结构、符号能量、功率、速率和差错概率。 8. 带限载波传输的收发结构、该传输体制（特别是升余弦基带成型时）的带宽、速率、功率、符号能量和差错概率互算。 9. 基带成型使用升余弦滤波时，由 \(R_b\) 和带通范围，计算 \(M,\alpha\) . 10. 计算线性调制的功率谱，并判断是否存在线谱。

波形信道概述¶

电平是一个物理量，但不能脱离物理实体存在。电平的物理实体就是电压信号的波形，例如：用一段时间的电压 \(+V\) 表示电平 \(A\) ，用一段时间的电压 \(-V\) 表示电平 \(-A\) .

电平：时间离散，对于一个电平来说，没有“时间”的概念。波形：即使只传输一个电平，也存在时间轴，有时、频的概念。

本课程专注于线性调制，即当只传一个符号时，波形可统一表示为：

\[ x(t)=xp(t) \]

\(p(t)\) 称为成形脉冲 pulse（一般需要归一化，便于分析）。我们要传输的波形 \(x(t)\) 就是使用 \(x\) 调制 \(p(t)\) 脉冲得到。

在《通信与网络》课程中，我们遇到的波形都是时域有限的能量信号（因为不同符号分时传输），因此能量信号的能量为：

\[ E=\int_{-\infty}^{+\infty}S_X(f)\mathrm{d}f=R_X(0)=\int_{-\infty}^{+\infty}|x(t)|^2\mathrm{d}t \]

因此发送端传输波形 \(x(t)\) 的信号能量：

\[ E_s=\int_{-\infty}^{+\infty}|x(t)|^2\mathrm{d}t=\mathbb{E}(|x|^2)\int_{-\infty}^{+\infty}p^2(t)\mathrm{d}t \]

在 \(p(t)\) 能量归一化 \(\int_{-\infty}^{+\infty}p^2(t)\mathrm{d}t=1\) 条件下，一个符号对应波形传输的能量 \(E_s\) 就等于电平传输的能量 \(\mathbb{E}(|x|^2)\) .

Tip

由于非归一化的存在，我们在讨论符号能量、bit 能量时应该指明是发送端还是接收端。

加型高斯白噪声信道¶

\[ \begin{matrix} & z(t) & \\ & \downarrow & \\ x(t) \longrightarrow & \oplus & \longrightarrow y(t)=x(t)+z(t) \end{matrix} \]

与前面讨论的香农公式、电平信道不同，这里的噪声 \(z(t)\) 为一个随机过程，是高斯白噪声。其性质为：

“高斯”：任意时刻的抽样序列 \(z(t_1),z(t_2),\cdots,z(t_N)\) 服从零均值联合高斯分布。
“白”：任意不同时刻的噪声不相关（根据高斯分布的性质，不相关能推出独立），其双边功率谱密度为常数 \(S_z(f)=\dfrac{n_0}{2}\) ，自相关函数为 \(R_z(\tau)=\dfrac{n_0}{2}\delta(t)\) .

因此，如果直接对高斯白噪声进行抽样，其方差为无穷大 \(\mathbb{E}(z^2(t_i))=R_z(0)=+\infty\) . 需要进行线性处理（滤波）之后，才能得到有限方差。

令等效电平噪声 \(z = \int_{-\infty}^{\infty} z(t)g(t)\mathrm{d}t\) ：

\[ \begin{align*} \mathbb{E}\{z^2\} &= \mathbb{E}\left\{\int_{-\infty}^{\infty} z(t)g(t)\mathrm{d}t \times \int_{-\infty}^{\infty} z(\tau)g(\tau)\mathrm{d}\tau\right\} \\ &= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \mathbb{E}\{z(t)z(\tau)\}g(t)g(\tau)\mathrm{d}t\mathrm{d}\tau \\ &= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \frac{n_0}{2} \delta(t - \tau) g(t)g(\tau)\mathrm{d}t\mathrm{d}\tau \\ &= \frac{n_0}{2} \int_{-\infty}^{\infty} g^2(t)\mathrm{d}t \quad \end{align*} \]

即高斯白噪声经过滤波之后，可以等效为电平信道传输中的高斯噪声 \(z \sim \mathcal{N}\left(0, \displaystyle\frac{n_0}{2} \int_{-\infty}^{\infty} g^2(t)\mathrm{d}t\right)\) .

最佳接收（匹配滤波）¶

通过处理，将接收波形 \(y(t)\) 映射到一个接收电平 \(y\) ，使得 \(y\) 中信号能量尽量大，噪声方差尽量小，信噪比最大化。

直接抽样 \(y=y(t_i)\) ？不行！因为任意时刻噪声方差无穷大。

考虑对波形进行积分，这样信号能量会累加，而噪声会正负抵消，效果应该较好。

\[ \begin{matrix} & z(t) & \\ & \downarrow & \\ x \overset{p(t)}{\longrightarrow} x(t) & \longrightarrow & y(t) \overset{g(t)}{\longrightarrow} y \end{matrix} \]

实电平波形传输最佳接收¶

虽然波形 \(p(t),g(t)\) 归一化后分析简单，但是很多时候我们遇到的都是没有归一化的情况，如果全部手动归一化很容易混淆各个系数的关系。因此我们考虑最一般的情况，能够让我们理解这个问题的本质（此处不一定严谨，因为积分可能发散）：

\[ \begin{align*} y&=\int_{-\infty}^{+\infty}y(t)g(t)\mathrm{d}t \\ &=\int_{-\infty}^{+\infty}x(t)g(t)\mathrm{d}t + \int_{-\infty}^{+\infty}z(t)g(t)\mathrm{d}t \\ &=x\int_{-\infty}^{+\infty}p(t)g(t)\mathrm{d}t + \int_{-\infty}^{+\infty}z(t)g(t)\mathrm{d}t \\ &= x\int_{-\infty}^{+\infty}p(t)g(t)\mathrm{d}t+z \end{align*} \]

根据之前的分析，等效电平噪声 \(z = \displaystyle\int_{-\infty}^{\infty} z(t)g(t)\mathrm{d}t \sim \mathcal{N}\left(0,\frac{n_0}{2} \int_{-\infty}^{\infty} g^2(t)\mathrm{d}t\right)\) .

此处将二进制和多进制的实电平传输放在一起讨论，因为本质是相同的。发送电平 \(x\) 从电平集合 \(\mathcal{A}\) 中取值，一般情况为 \(\mathcal{A}=\{-(M-1)A,\cdots,-A,A,\cdots,(M-1)A\}\) . 从发送端的角度，相邻电平的间隔为 \(2A\) ，那么电平到判决门限的距离理应为 \(A\) ，但是经过非归一化的波形 \(g(t)\) 调制，接收端判决门限到电平的距离变为 \(A'=A\displaystyle\int_{-\infty}^{+\infty}p(t)g(t)\mathrm{d}t\) .

发送端的波形能量为 \(E_s=\displaystyle\int_{-\infty}^{+\infty}x(t)^2\mathrm{d}t=\mathbb{E}(x^2)\int_{-\infty}^{+\infty}p^2(t)\mathrm{d}t\) .

接收端的波形能量为 \(\mathbb{E}(x^2)\left(\displaystyle\int_{-\infty}^{+\infty}p(t)g(t)\mathrm{d}t\right)^2\) ，噪声能量为 \(\displaystyle\frac{n_0}{2} \int_{-\infty}^{\infty} g^2(t)\mathrm{d}t\) . 因此接收端信噪比为：

\[ \mathrm{SNR}=\frac{\mathbb{E}(x^2)\left(\displaystyle\int_{-\infty}^{+\infty}p(t)g(t)\mathrm{d}t\right)^2}{\displaystyle\frac{n_0}{2} \int_{-\infty}^{\infty} g^2(t)\mathrm{d}t} \]

根据 Cauchy-Schwarz 不等式， \(\displaystyle\left(\int_{-\infty}^{+\infty}p(t)g(t)\mathrm{d}t\right)^2\leqslant \int_{-\infty}^{\infty} p^2(t)\mathrm{d}t \cdot \int_{-\infty}^{\infty} g^2(t)\mathrm{d}t\) 对于任意接收波形 \(g(t)\) 成立，因此：

\[ \mathrm{SNR}_{\max}=\frac{\mathbb{E}(x^2)}{n_0/2}\int_{-\infty}^{+\infty}p^2(t)\mathrm{d}t \]

信噪比取最大值时，即为最佳接收，取等条件为 \(g(t)=\lambda p(t),\;\lambda>0\) ，即 \(g(t),p(t)\) 的波形相同，仅有系数的区别，且这个系数会在接收端同时放缩信号和噪声的能量，因此不会影响接收端的信噪比和差错概率。

如果进行归一化，就有 \(g(t)=p(t),\;\displaystyle\int_{-\infty}^{+\infty}p^2(t)\mathrm{d}t=1,\;\mathrm{SNR}=\dfrac{\mathbb{E}(x^2)}{n_0/2}\) .

从信号矢量空间的角度来看， \(\displaystyle\int_{-\infty}^{+\infty}p(t)g(t)\mathrm{d}t\) 相当于两个信号的内积，内积越大，二者波形越“相似”。

收发联合模型¶

最佳接收时，我们不妨令 \(g(t)=p(t)\) ，接收端 \(y=\displaystyle\int_{-\infty}^{+\infty}y(t)g(t)\mathrm{d}t\) ，可以使用“乘法器+积分器”实现。但是我们注意到这是一个相关操作，因此最常用的是“相关 = 滤波 + 抽样”，使用 \(p(T-t)\) 作为滤波器：

\[ y(t)\longrightarrow\boxed{p(T-t)}\longrightarrow\tilde{y}(t)\overset{t=T}{\longrightarrow} y \]

因此有：

\[ \begin{align*} \tilde{y}(t) &= y(t) * p(T-t) \\ &= \int_{-\infty}^{\infty} y(\tau)p(T-(t-\tau))d\tau \\ &= \int_{-\infty}^{\infty} y(\tau)p(\tau+T-t)d\tau \end{align*} \]

在 \(t=T\) 时刻抽样（保证因果性）：

\[ \tilde{y}(T) = \int_{-\infty}^{\infty} y(\tau)p(\tau+T-T)d\tau = \int_{-\infty}^{\infty} y(t)p(t)dt \]

在频域上，若 \(P(f)=\mathcal{F}[p(t)]\) ，则 \(\mathcal{F}[p(T-t)]=e^{-\mathrm{j}2\pi fT}P^*(f)\) .

发送端，注意到 \(x(t)=xp(t)=x\delta(t)*p(t)\) ，相当于用 \(x\) 调制一个单位冲激函数，然后再通过滤波器 \(p(t)\) .

则收发两端都可以表示为滤波器形式：

\[ \begin{matrix} & z(t) & \\ & \downarrow & \\ x\delta(t) \longrightarrow \boxed{p(t)} \longrightarrow & \oplus & \longrightarrow \boxed{p(T-t)} \overset{t=T}{\longrightarrow} y(t) \end{matrix} \]

若仅考虑信号部分，不考虑噪声，则中间两个滤波器可以合成为一个滤波器：

\[ \begin{gather*} x\delta(t) \longrightarrow \boxed{h(t)} \overset{t=T}{\longrightarrow} y \\ h(t)=p(t)*p(T-t),\quad H(f)=P(f)e^{-\mathrm{j}2\pi fT}P^*(f)=|P(f)|^2e^{-\mathrm{j}2\pi fT} \end{gather*} \]

无失真传输准则¶

之前我们只讨论了发送和接收一个符号的过程，但是由于波形传输具有时间的概念，因此且发送符号存在先后顺序，因此我们还需要考虑发送和接收各个符号时的时序，保证它们对应的波形不发生重叠和失真。例如，传输一个电平符号之后，我们会在一段时间 \(\Delta t\) 之后重新使用信道传输下一个符号。

那么信道使用间隔 \(\Delta t\) 最小为多少时，能够信号让 \(x_0\delta(t),\;x_1\delta(t-T)\) 在发送端对应的波形 \(x_0h(t),\;x_1h(t-T)\) 在各自的抽样点处不相互干扰？

问题进一步转化为：以间隔 \(T\) 用冲激串调制符号得到的 \(\displaystyle\sum_{k=-\infty}^{+\infty}x_k\delta(t-kT)\) ，经过 \(h(t)\) 之后，在抽样点 \(t=kT\) 互不干扰，则 \(h(t)\) 应满足什么条件？

从时域入手，抽样点无失真意味着 \(\displaystyle\sum_i x_ih((k-i)T)=x_k\) ，我们很容易得到：

\[ h(kT)=\delta_k=\begin{cases} 1,& k=0 \\ 0,& k=\pm 1,\pm 2,\cdots \end{cases} \]

从频域入手，根据 \(h(t)\times\displaystyle\sum_{k=-\infty}^{+\infty}\delta(t-kT)=\delta(t)\) 我们可以得到 Nyquist 准则：

\[ \sum_{n=-\infty}^{+\infty}H\left(f+\frac{n}{T}\right) =\sum_{n=-\infty}^{+\infty}H\left(f+nR_s\right)=T \]

其中 \(R_s=\dfrac{1}{T}\) 即为符号速率，是单位时间内传输的符号个数。

几何解释：频谱 \(H(f)\) 以 \(R_s\) 为周期平移复制之后得到 \(H(f+nR_s)\) ，所有这样的平移结果 \(H(f+nR_s)\) 叠加后，得到的新函数是一个关于 \(f\) 的常数函数。

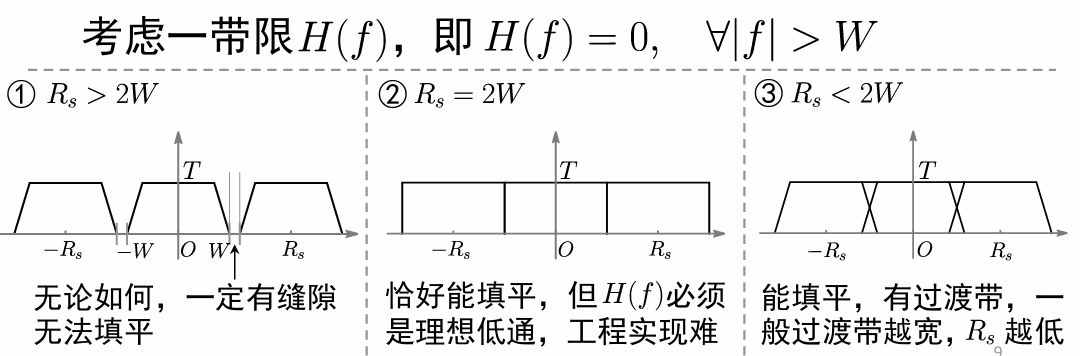
Nyquist 准则最重要的应用，是把通信波形（或信道）的带宽要求，与符号速率联系起来。因此我们有带宽要求：

\[ R_s\leqslant 2W \]

直观理解：理想情况下通信带宽 \(W\) 越大越好。若带宽 \(W\) 过小，高频分量不足， \(h(t)\) 在时域变化缓慢，难以在 \(t=T=\dfrac{1}{T_s}\) 的位置减小 0。反过来，符号速率 \(R_s\) 不能太快，应该尽量等到上一个符号的波形减小至 0 之后再发送下一个信号。

定义单位带宽内支持的通信速率为 \(\eta=\dfrac{R_b}{W}=\dfrac{R_s}{W}\log_2 M\leqslant 2\log_2 M,\quad M=|\mathcal{A}|\) .

升余弦滤波系统¶

根据之前讨论的 \(H(f)\) 应该满足的条件，我们可以构造这样的一个函数 \(\hat{H}(f)\) ：

\(\hat{H}(f)=\hat{H}(-f)\) ，为偶函数。
\(\hat{H}(f)=0,\;|f|>R_s\) ，带限于 \(R_s\) .
\(\hat{H}\left(\dfrac{R_s}{2}-f\right)=-\hat{H}\left(\dfrac{R_s}{2}+f\right)\) ，关于 \(f=\dfrac{R_s}{2}\) 中心对称。

然后根据 \(\hat{H}(f)\) 构造出 \(H(f)\) ：

\[ H(f)=\begin{cases} 1+\hat{H}(f),& |f|<\dfrac{R_s}{2} \\ \hat{H}(f),& \dfrac{R_s}{2}\leqslant |f| \leqslant R_s \end{cases} \]

这样的 \(H(f)\) 一定满足 Nyquist 准则。

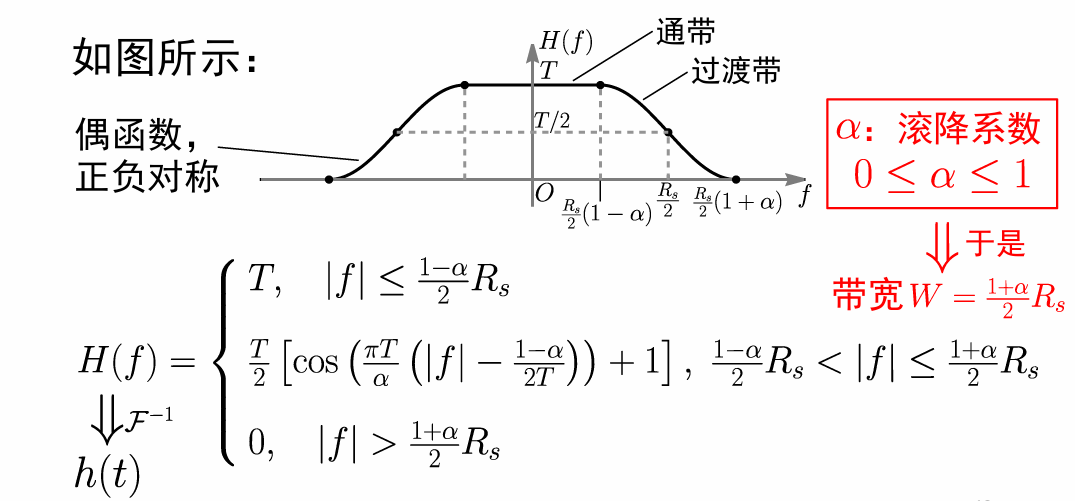
而实际中，我们最常使用余弦函数的半个周期作为 \(H(f)\) 的过渡带，称为升余弦滤波系统。

经傅里叶反变换得到其冲激响应 \(h(t)\) 为：

\[ h(t) = \frac{\sin(\pi R_s t)}{\pi R_s t} \frac{ \cos(\pi \alpha R_s t)}{1 - 4(\alpha R_s t)^2} \]

滚降系数 \(\alpha\) 衡量余弦波形下降的快慢，其值越小，波形下降地越快。 \(\alpha=0\) 时为理想低通滤波器， \(\alpha=1\) 为通带消失，全部是过渡带，为一整个周期的余弦函数。

由上图可知 \(W=\dfrac{1+\alpha}{2}R_s,\;R_s=\dfrac{2W}{1+\alpha}\) ，频谱效率为：

\[ \eta=\frac{R_s \log_2 M}{W}=\frac{2\log_2 M}{1+\alpha} \]

通常有一类典型题目是：给定 \(R_b,W\) 求 \(\alpha,M\) ，但这是一个欠定问题，我们有约束 \(\dfrac{R_b}{W}=\dfrac{\log_2 M}{1+\alpha},\;0<\alpha\leqslant 1\) . 有这 2 个约束，我们通常会得到多对 \((\alpha,M)\) 的解。

数字基带传输¶

根据刚才的分析，我们使用匹配滤波来实现最佳接收：

\[ \begin{matrix} & z_k(t) & \\ & \downarrow & \\ x_k\delta(t) \longrightarrow \boxed{p(t)} \longrightarrow & \oplus & \longrightarrow \boxed{p(T-t)} \overset{t=T}{\longrightarrow} y_k(t) \longrightarrow y_k \end{matrix} \]

上述波形传输可以等效为电平传输 \(y_k=x_k+z_k\) .

发送端 \(x_k\in\mathcal{A},\;E_s=\displaystyle\mathbb{E}(x^2)\int_{-\infty}^{+\infty}p^2(t)\mathrm{d}t\) 。接收端信号能量变为 \(\displaystyle\mathbb{E}(x^2)\left(\int_{-\infty}^{+\infty}p^2(t)\mathrm{d}t\right)^2\)

噪声为独立同分布的高斯随机变量 \(z_k\overset{i.i.d.}{\sim}\mathcal{N}\left(0,\displaystyle\frac{n_0}{2} \int_{-\infty}^{\infty} p^2(t)\mathrm{d}t\right)\) .

接收端信噪比为：

\[ \mathrm{SNR}=\frac{E_s}{n_0/2}\int_{-\infty}^{+\infty}p^2(t)\mathrm{d}t \]

矩形包络载波传输¶

之前讨论的基带传输，其通信信号在 0 频率附近，带限于 \(W\) （工程上常在kHz~MHz数量级）。

在无线通信等系统中，我们常希望通信信号的主要功率（能量）集中在载波 \(f_c\) 附近（工程上常在GHz数量级），原因是：

\(f_c\) 附近有好的信道特性（天线尺寸、衍射绕射尺寸）。
在不同 \(f_c\) 上传输，可以实现多个通信链路的空间共享，同时传输。

将之前讨论的成形脉冲 \(p(t)\) 具体化为载波频率为 \(f_c\) 的余弦函数，符号发送周期为 \(T\) ，应满足 \(f_cT\in\mathbb{N}^+\) 为正整数。我们仍然考虑没有归一化的最一般情况：

\[ p(t)=\beta\cos(2\pi f_c t)\times\mathbb{I}\{0\leqslant t<T\},\quad \int_{-\infty}^{+\infty}p^2(t)\mathrm{d}t=\beta^2\frac{T}{2} \]

发送端调制波形为 \(x(t)=xp(t)\) .

称为矩形包络载波传输的原因是示性函数 \(\mathbb{I}\{0\leqslant t<T\}\) 本身就是一个矩形波。

二进制单路载波传输¶

称为 BPSK ，二进制相移键控。

发送端调制波形：

\[ x(t)=x\cdot\beta\cos(2\pi f_c t)\times\mathbb{I}\{0\leqslant t<T\},\quad x\in\{-A,A\} \]

其能量为 \(E_s=\displaystyle\int_0^Tx^2(t)\mathrm{d}t=\mathbb{E}(x^2)\cdot\beta^2\frac{T}{2}=A^2\left(\beta^2\frac{T}{2}\right)\) . 每 bit 能量为 \(E_b=E_s\) .

通信信号的功率为 \(P=\dfrac{E_s}{T}=E_sR_s=E_bR_b\) .

最佳接收时，接收端使用 \(g(t)=\gamma\cos(2\pi f_c t)\times\mathbb{I}\{0\leqslant t<T\}\) ，则等效为电平信道传输：

\[ \begin{align*} y&=\int_0^T y(t)g(t)\mathrm{d}t \\ &=x\int_0^T p(t)g(t)\mathrm{d}t + \int_0^Tz(t)g(t)\mathrm{d}t \\ &=x\left(\beta\gamma\frac{T}{2}\right)+z \end{align*} \]

其中等效噪声 \(z\sim \mathcal{N}\left(0,\displaystyle\frac{n_0}{2} \int_0^T g^2(t)\mathrm{d}t\right)= \mathcal{N}\left(0,\displaystyle\frac{n_0}{2} \cdot\gamma^2\frac{T}{2}\right)\) .

接收端信噪比为：

\[ \mathrm{SNR}=\frac{\mathbb{E}(x^2)\left(\displaystyle\int_{-\infty}^{+\infty}p(t)g(t)\mathrm{d}t\right)^2}{\displaystyle\frac{n_0}{2} \int_{-\infty}^{\infty} g^2(t)\mathrm{d}t}=\frac{A^2\left(\beta\gamma\dfrac{T}{2}\right)^2}{\dfrac{n_0}{2}\gamma^2\dfrac{T}{2}}=\frac{A^2}{n_0/2}\left(\beta^2\frac{T}{2}\right) \]

Note

这里接收端信噪比显然是和接收时使用的载波系数 \(\gamma\) 无关、而与发射载波系数 \(\beta\) 有关，因为只有信号经过了发射载波 \(p(t)\) ，对信号进行了实质性的放缩。而信号和噪声同时经过了接收载波 \(g(t)\) ，是同比例放缩，这一步对信噪比没有影响。

考虑误符号率时，我们还是从更本质的“接收端等效电平和判决门限的距离”来入手：

\[ A'=A\left(\beta\gamma\frac{T}{2}\right),\quad \sigma'=\sqrt{\frac{n_0}{2} \cdot\gamma^2\frac{T}{2}},\quad P_s=Q\left(\frac{A'}{\sigma'}\right)=Q\left(A\beta\sqrt{\frac{T}{n_0}}\right),\quad P_b=P_s \]

多进制单路载波传输¶

称为 MPAM， \(M\) 进制脉冲幅度调制。

分析过程与 BPSK 完全类似。

发送端调制波形：

\[ x(t)=x\cdot\beta\cos(2\pi f_c t)\times\mathbb{I}\{0\leqslant t<T\},\quad x\in\{-(M-1)A,\cdots,-A,A,\cdots,(M-1)A\} \]

其能量为 \(E_s=\displaystyle\int_0^Tx^2(t)\mathrm{d}t=\mathbb{E}(x^2)\cdot\beta^2\frac{T}{2}=\dfrac{M^2-1}{3}A^2\left(\beta^2\frac{T}{2}\right)\) . 每 bit 能量 \(E_b=\dfrac{E_s}{\log_2 M}\) .

通信信号的功率为 \(P=\dfrac{E_s}{T}=E_sR_s=E_bR_b,\; R_s=\dfrac{1}{T},\; R_b=R_s\log_2 M\) .

最佳接收时，接收端使用 \(g(t)=\gamma\cos(2\pi f_c t)\times\mathbb{I}\{0\leqslant t<T\}\) ，则等效为电平信道传输：

\[ \begin{align*} y&=\int_0^T y(t)g(t)\mathrm{d}t \\ &=x\int_0^T p(t)g(t)\mathrm{d}t + \int_0^T z(t)g(t)\mathrm{d}t \\ &=x\left(\beta\gamma\frac{T}{2}\right)+z \end{align*} \]

其中等效噪声 \(z\sim \mathcal{N}\left(0,\displaystyle\frac{n_0}{2} \int_{-\infty}^{\infty} g^2(t)\mathrm{d}t\right)= \mathcal{N}\left(0,\displaystyle\frac{n_0}{2} \cdot\gamma^2\frac{T}{2}\right)\) .

接收端信噪比为：

\[ \mathrm{SNR}=\frac{\mathbb{E}(x^2)\left(\displaystyle\int_{-\infty}^{+\infty}p(t)g(t)\mathrm{d}t\right)^2}{\displaystyle\frac{n_0}{2} \int_{-\infty}^{\infty} g^2(t)\mathrm{d}t}=\frac{\dfrac{M^2-1}{3}A^2\left(\beta\gamma\dfrac{T}{2}\right)^2}{\dfrac{n_0}{2}\cdot\gamma^2\dfrac{T}{2}}=\frac{M^2-1}{3}\frac{A^2}{n_0/2}\left(\beta^2\frac{T}{2}\right) \]

误符号率：

\[ \begin{gather*} A'=A\left(\beta\gamma\frac{T}{2}\right),\quad \sigma'=\sqrt{\frac{n_0}{2} \cdot\gamma^2\frac{T}{2}} \\ P_s=\frac{2M-2}{M}Q\left(\frac{A'}{\sigma'}\right)=\frac{2M-2}{M}Q\left(A\beta\sqrt{\frac{T}{n_0}}\right),\quad P_b\approx\frac{P_s}{\log_2 M} \end{gather*} \]

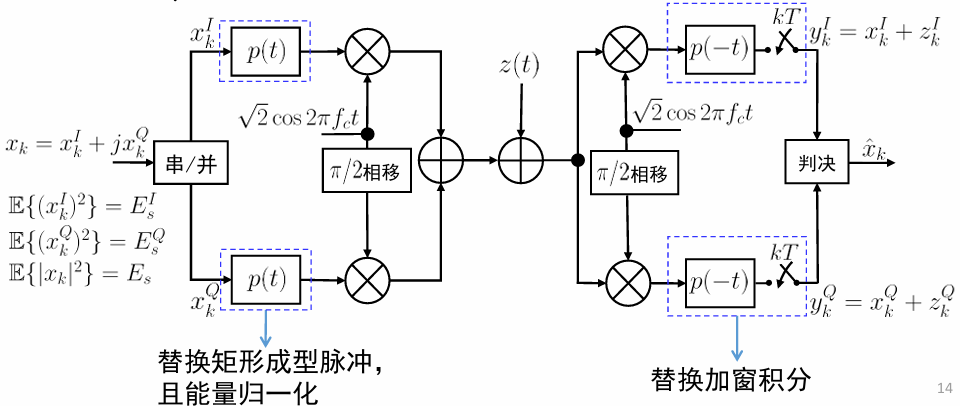
I,Q 路载波传输¶

在信号的矢量空间中 \(\cos(2\pi f_ct),\;\sin(2\pi f_ct)\) 具有天然的正交关系。因此能够同时传输 I,Q 两路信号而互不串扰。 \(x(t)=x_I(t)+\mathrm{j}x_Q(t),\;x_I,x_Q\in\mathcal{A}\) ：

\[ \begin{align*} x_I(t)&=x_I\cdot\beta\cos(2\pi f_c t)\times\mathbb{I}\{0\leqslant t<T\} \\ x_Q(t)&=x_Q\cdot\beta\sin(2\pi f_c t)\times\mathbb{I}\{0\leqslant t<T\} \end{align*} \]

接收端为：

\[ \begin{align*} y_I&=\int_{-\infty}^{+\infty}y_I(t)\cdot \left(\gamma\cos(2\pi f_c t)\times\mathbb{I}\{0\leqslant t<T\}\right) \mathrm{d}t \\ y_Q&=\int_{-\infty}^{+\infty}y_Q(t)\cdot \left(\gamma\sin(2\pi f_c t)\times\mathbb{I}\{0\leqslant t<T\}\right) \mathrm{d}t \end{align*} \]

对其中一路的最佳接收，本身就消除了另一路的干扰，因为 \(\int_0^T\sin(2\pi f_ct)\cos(2\pi f_c t)\mathrm{d}t=0\) .

因此载波传输中 I,Q 两路可以独立传输 \(x_I,\;x_Q\) ，互不干扰。发送的复电平为 \(x=x_I+\mathrm{j}x_Q\) . 发送端信号能量为 \(E_s=\mathbb{E}(|x|^2)\cdot \beta^2\dfrac{T}{2}\) .

通信功率 \(P=\dfrac{E_s}{T}=E_sR_s=E_bR_b=\dfrac{E_b\log_2 M}{T}\) .

沿用之前的分析得到等效复电平信道： \(y_I=x_I\left(\beta\gamma\dfrac{T}{2}\right)+z_I,\;y_Q=x_Q\left(\beta\gamma\dfrac{T}{2}\right)+z_Q\) .

I,Q 两路等效电平噪声分别为 \(z_I\sim \mathcal{N}\left(0,\displaystyle\frac{n_0}{2} \cdot\gamma^2\frac{T}{2}\right),\;z_Q\sim \mathcal{N}\left(0,\displaystyle\frac{n_0}{2} \cdot\gamma^2\frac{T}{2}\right)\) .

因此复噪声 \(z_I+\mathrm{j}z_Q=z\sim \mathcal{CN}\left(0,\displaystyle n_0 \cdot\gamma^2\frac{T}{2}\right)\) .

接收端信噪比：

\[ \mathrm{SNR}=\frac{\mathbb{E}(|x|^2)\cdot \left(\beta\gamma\dfrac{T}{2}\right)^2}{n_0 \cdot\gamma^2\dfrac{T}{2}}=\frac{\mathbb{E}(|x|^2)}{n_0}\cdot\left(\beta^2\frac{T}{2}\right) \]

M-QAM（ \(M\) 进制正交幅度调制），类比电平信道。

发送端复电平集合：

\[ \mathcal{A}=\{x_I+\mathrm{j}x_Q|x_i,x_Q\in\{-(\sqrt{M}-1)A,\cdots,-A,A,\cdots,(\sqrt{M}-1)A\}\} \]

对于电平符号 \(\mathbb{E}(|x|^2)=\dfrac{2(M-1)}{3}A^2\) .

接收端等效电平和判决门限的距离分别为：

\[ A'=A\left(\beta\gamma\frac{T}{2}\right),\quad \sigma'=\sqrt{\frac{n_0}{2} \cdot\gamma^2\frac{T}{2}},\quad \frac{A'}{\sigma'}=A\beta\sqrt{\frac{T}{n_0}} \]

误符号率：

\[ P_s\approx 4\left(1-\frac{1}{\sqrt{M}}\right)Q\left(\dfrac{A'}{\sigma'}\right),\quad P_b\approx\frac{P_s}{\log_2M} \]

M-PSK（ \(M\) 进制相位键控），同样可以类比电平信道。

\[ \mathcal{A}=\left\{A,Ae^{\mathrm{j}\theta},Ae^{\mathrm{j}2\theta},\cdots, Ae^{\mathrm{j}(M-1)\theta}\right\},\quad \theta=\frac{2\pi}{M} \]

对于电平符号 \(\mathbb{E}(|x|^2)=A^2\) .

接收端等效电平和判决门限的距离分别为：

\[ A'=A\left(\beta\gamma\frac{T}{2}\right),\quad \sigma'=\sqrt{\frac{n_0}{2} \cdot\gamma^2\frac{T}{2}},\quad \frac{A'}{\sigma'}=A\beta\sqrt{\frac{T}{n_0}} \]

误符号率：

\[ P_s=2Q\left(\frac{A'}{\sigma'}\sin\frac{\pi}{M}\right),\quad P_b=\frac{P_s}{\log_2 M} \]

带限载波传输¶

之前讨论的矩形包络载波传输，优点是分析和实现简单，但是由于使用的基带信号也就是矩形波时域有限、频域无限，发送的载波信号带宽不受限制，在实际的通信系统中无法直接使用。且矩形包络载波传输要求 \(f_cT\in\mathbb{N}^+\) ，若给定 \(f_s\) 则 \(T,R_s\) 不能任意选择。

改进想法：设计一种载波传输方案，只使用 \(f_c\) 附近的带通信道 \(||f|-f_c|\leqslant W\) ，且 \(f_cT\) 不必是正整数。

单路带限载波传输¶

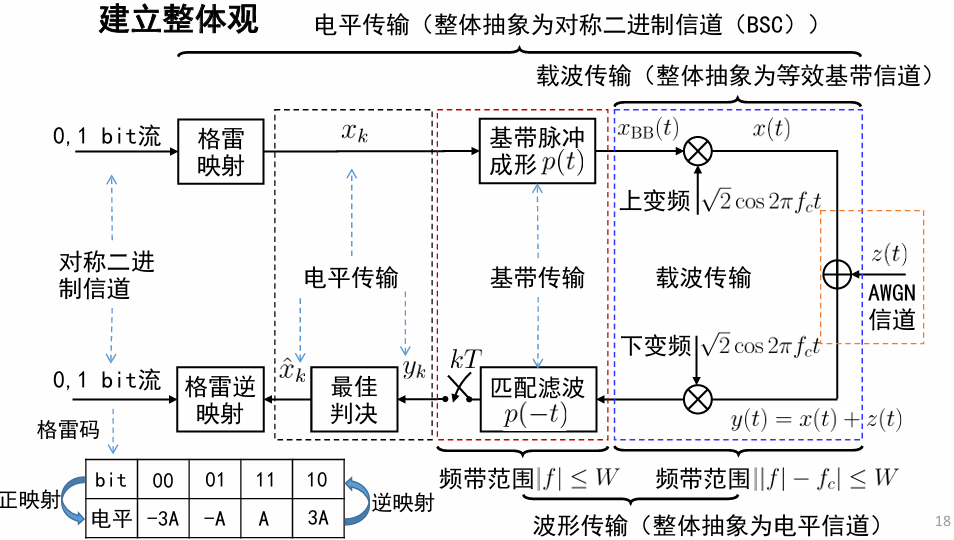
基于频谱搬移的方案设计：

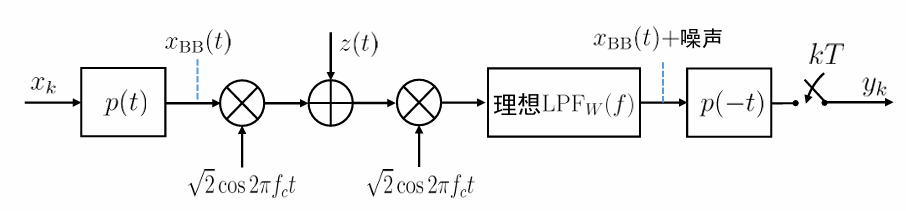
对 \(x_{BB}(t) = \sum_k x_k p(t - kT)\) 乘以 \(\sqrt{2}\cos(2\pi f_c t)\) 搬移到带通信道 \([-f_c - W, -f_c + W] \cup [f_c - W, f_c + W]\) 中。
对 \(y(t)\) 再乘以 \(\sqrt{2}\cos(2\pi f_c t)\)，再次搬移后落在基带 \(|f| \leqslant W\) 和高频带 \(||f| - 2f_c| \leqslant W\) 中。
用带宽 \(W\) 的理想低通滤掉高频分量，恢复信号分量 \(x_{BB}(t)\)，再做最佳接收。

注意到，接收端的理想低通 \(\mathrm{LPF}_W(f),\;p(-t)\) 可以简化为一个 \(p(-t)\) ，理由是： \(\mathcal{F}[p(-t)] = P^*(f)\) ，由于 \(\forall |f|>W,\;P(f) = 0\) ，故此时 \(P^*(f) = 0,\;H(f) = |P(f)|^2 = 0\) 。因此，带宽 \(W\) 的理想低通对 \(P^*(f)\) 无影响，或者说 \(P^*(f)\) 本身就带限，相当于一个低通滤波器，也能成功滤掉 \(\pm 2f_c\) 处的高频分量。

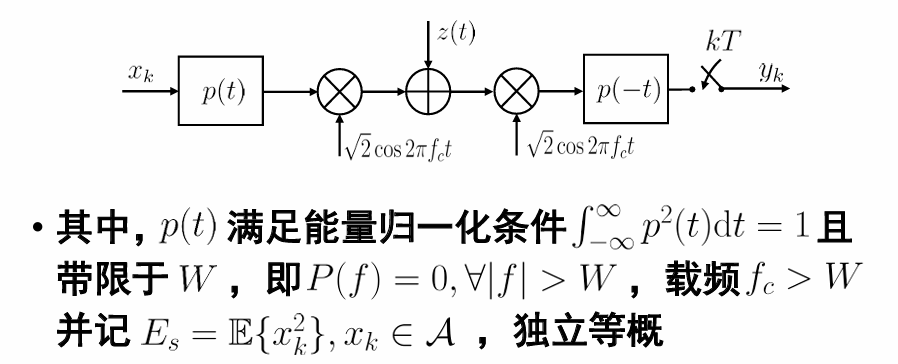
因此，最终带限传输方案为：

好像就是把基带信号 \(p(t)\) 从不带限换成带限的，其他的好像没变？关于信噪比和差错分析似乎也和之前一样？

结论：单路带限载波传输的带宽 \(B = 2W\) ，符号速率 \(R_s = \dfrac{1}{T}\) ，bit 速率 \(R_b = R_s \log_2 M = \dfrac{\log_2 M}{T},\;M = |\mathcal{A}|\) .

符号能量 \(E_s = E_b \log_2 M\) ，功率 \(P = E_s R_s = \dfrac{E_s}{T} = \dfrac{E_b \log_2 M}{T} = E_b R_b\) .

其等效电平信道分析，和前面的矩形包络载波传输相同。

I,Q 路带限载波传输¶

\(\sin(2\pi f_c t)\) 同样可以把基带信号搬移到载频 \(f_c\) 附近。设计 I,Q 路带限载波传输方案：

I,Q 路带限载波传输的带宽 \(B = 2W\) ，复符号速率 \(R_s = \dfrac{1}{T}\) ，bit 速率 \(R_b = R_s \log_2 M = \dfrac{\log_2 M}{T},\;M = |\mathcal{A}|\) .

符号能量 \(E_s = E_s^I + E_s^Q\) ，功率 \(P = E_s R_s = \dfrac{E_s}{T} = \dfrac{E_b \log_2 M}{T} = E_b R_b\) .

载波传输的频谱效率：

载波传输占用的频带 \(B\) 为基带的 2 倍，由无失真准则 \(\dfrac{R_s}{W} \leq 2\) ，得到：

\[ \eta = \frac{R_b}{B} = \frac{R_b}{2W} = \frac{R_s \log_2 M}{2W} \leqslant \log_2 M \]

若采用升余弦滤波系统生成基带波形，则因 \(R_s = \dfrac{2W}{1+\alpha}\) 有：

\[ \eta = \frac{R_s \log_2 M}{2W} = \frac{\log_2 M}{1+\alpha},\quad M = |\mathcal{A}| \]

似乎相比于基带信号的 \(\eta=\dfrac{2\log_2 M}{1+\alpha}\) ，载波的频谱效率减小了一半。

对频谱效率 \(\eta\) 折半的理解

同样带宽下支持的 \(R_s\) 虽然减半，但 \(x_k = x_k^I + \mathrm{j}x_k^Q\) 包含 I,Q 两路符号。同样分路噪声 \(\sigma^2 = \dfrac{n_0}{2}\) ，同样可靠性要求 \(P_s, P_b\) 下，可同时传 I,Q 两路符号，如一路 \(M\) -QAM 等价两路 \(\sqrt{M}\) -PAM，总的频谱效率不变。但若只用 \(\cos(\cdot)\) 或 \(\sin(\cdot)\) 一路，则确实会损失一半频谱效率。

典型题型是：在升余弦滤波系统中，给定 bit 速率 \(R_b\) 和带通范围 \([f_{\min},f_{\max}]\) ，求 \(M,\alpha\) .

求解关键：载频 \(f_c\) 位于频带中间 \(f_c=\dfrac{f_{\min}+f_{\max}}{2},\;B=f_{\max}-f_{\min}\) ，对应基带带宽为 \(W=\dfrac{f_{\max}-f_{\min}}{2}\) .

\[ \eta=\frac{R_b}{B}=\frac{R_b}{f_{\max}-f_{\min}}=\frac{\log_2 M}{1+\alpha} \]

仍然是一个欠定问题，但是根据约束 \(0<\alpha\leqslant 1,\;\log_2 M\in\mathbb{N}^+\) ，我们可以求出多组 \((M,\alpha)\) .

基带信号功率谱¶

讨论功率谱是为了定量分析通信信号的功率在频域的分布，确定其对相邻无线电系统的潜在干扰，及其自身的抗干扰能力，例如：

超宽带系统 UWB 占用数 GHz 带宽，要避开其频带内的重要国防、医疗设施。
蜂窝通信中，一个蜂窝的六个相邻蜂窝用不同的频带，要考虑蜂窝间的带外泄露干扰

我们首先需要知道通信信号 \(x(t)\) 是否宽平稳，根据 \(x(t)=\sum_k x_k p(t-kT)\) ：

\[ \begin{align*} \mathbb{E}\{x(t)\} &= \mathbb{E}\{x_k\} \sum_k p(t - kT) \\ \tilde{R}(t+\tau,t) &= \mathbb{E}\left\{\sum_i x_i p(t+\tau - iT) \sum_k x_k p(t - kT)\right\} \\ &= \sum_i \sum_k \mathbb{E}\{x_i x_k\} p(t+\tau - iT) p(t - kT) \\ &= \sum_i \sum_k R_x[i-k] p(t+\tau - iT) p(t - kT) \\ \tilde{R}(t+\tau+T,t+T) &= \tilde{R}(t+\tau,t) \end{align*} \]

可见 \(x(t)\) 不是宽平稳的，而只是周期平稳的。我们利用其周期性适当地加窗平均，可得到近似的一维自相关函数：

\[ \bar{R}(\tau)=\frac{1}{T}\int_0^T\tilde{R}(t+\tau,t)\mathrm{d}t \]

因此通信信号的功率谱即为 \(S_X(f)=\mathcal{F}[\bar{R}(\tau)]\) .

定理：线性调制通信信号 \(x(t)=\sum_k x_k p(t-kT)\) 功率谱为

\[ S_X(f)=\frac{\sigma_x^2}{T}|P(f)|^2+\frac{m_x^2}{T^2}\sum_{k=\infty}^{+\infty}|P(\frac{n}{T})|^2\delta(f-\frac{n}{T}),\quad m_x=\mathbb{E}(x_k),\sigma_x^2=\mathbb{E}(x_k^2)-m_x^2 \]

上式中第一项为连续谱，第二项为线谱，线谱只有在电平符号 \(x_k\) 非零均值时才有。

载波信号功率谱¶

对基带信号 \(x(t)\) 乘以载波 \(\cos(2\pi f_ct)\) ，搬移频谱的同时，也搬移了功率谱。下式进行了归一化：

\[ x(t)\cdot\sqrt{2}\cos(2\pi f_ct) \Leftrightarrow \frac{1}{\sqrt{2}}[X(f-f_c)+X(f+f_c)] \Leftrightarrow \frac{1}{2}[S_X(f-f_c)+S_X(f+f_c)] \]

因此对一个单路载波信号：

\[ \begin{matrix} x_k \longrightarrow \boxed{P(f)} \longrightarrow x_{BB}(t) \longrightarrow & \otimes & \longrightarrow x(t) \\ & \uparrow & \\ & \sqrt{2}\cos(2\pi f_ct) & \end{matrix} \]

其中 \(x_BB(t)=\sum_k x_k p(t-kT)\) 基带信号功率谱我们已经求过，则：

\[ \begin{align*} S_X(f) = & \frac{\sigma_x^2}{2T} \left[|P(f - f_c)|^2 + |P(f + f_c)|^2\right] \qquad \text{连续谱} \\ & + \frac{m_x^2}{2T^2} \sum_{n=-\infty}^{+\infty} \left| P\left(\frac{n}{T}\right) \right|^2 \left[ \delta\left(f - f_c - \frac{n}{T}\right) + \delta\left(f + f_c - \frac{n}{T}\right) \right] \qquad \text{线谱} \end{align*} \]

需要注意：

对 QAM，I,Q 路电平独立（零均值、统计独立、功率正交），功率谱可直接叠加。
对 PSK，I,Q 路电平不独立，功率谱不能直接叠加，需要考虑联合谱和互相关项。

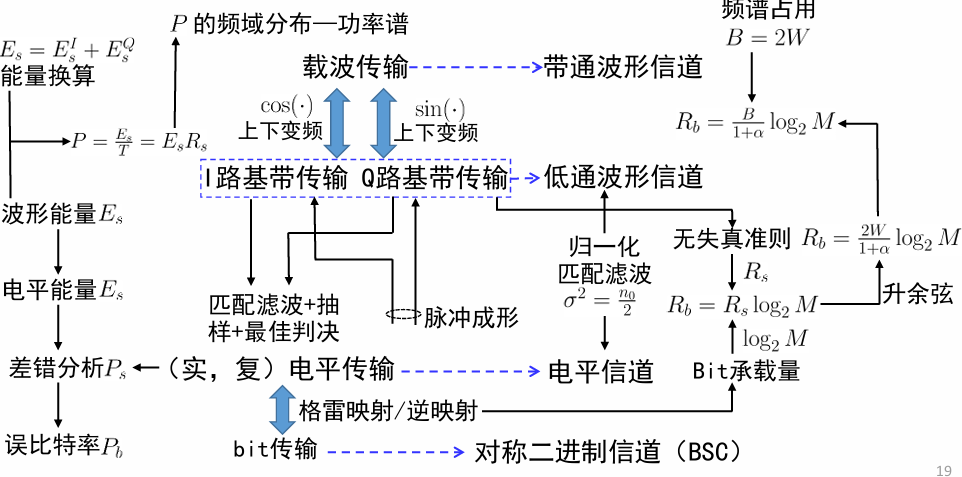
数字调制总结¶

附录 1¶

为了应付做题和考试，让我们研究一下单路载波波形传输的最一般情况：

\[ \begin{matrix} & & z(t) & & \\ & & \downarrow & & \\ x_k \longrightarrow \boxed{p(t)} \longrightarrow & \otimes & \longrightarrow \oplus \longrightarrow & \otimes & \longrightarrow \boxed{g(t)=\lambda p(-t)} \overset{t=kT}{\longrightarrow} y_k \\ & \uparrow & & \uparrow & \\ & \beta \cos(2\pi f_c t) & & \gamma\cos(2\pi f_c t) & \\ \end{matrix} \]

高斯白噪声 \(z(t)\sim\mathcal{N}(0,\dfrac{n_0}{2})\) .

其中，基带成形脉冲 \(p(t)\) 可以是矩形波（对应矩形包络载波传输），也可以是带限波，例如升余弦系统的成形波，时域无限频域有限（对应带限载波传输），接收端最佳接收匹配滤波 \(g(t)=\lambda p(-t),\; \lambda>0\) 和成形波 \(p(-t)\) 波形相同，仅有一个正系数的区别。

上述 4 个波形 \(p(t),\;g(t),\;\beta\cos(2\pi f_c t),\;\gamma\cos(2\pi f_c t)\) 的能量或者系数均不满足归一化，足以应对考试出现的各种情况。

假设 \(p(t)\) 的自相关函数为 \(h(t)=p(t)*p(-t)\) ，功率谱为 \(H(f)=\mathcal{F}[h(t)]=|P(f)|^2=S_P(f)\) ，则成形脉冲的能量为：

\[ \begin{align*} \int_{-\infty}^{+\infty} p^2(t)\mathrm{d}t&=h(0)=\int_{-\infty}^{+\infty}H(f)\mathrm{d}f=\lambda_1 \\ \int_{-\infty}^{+\infty} g^2(t)\mathrm{d}t&=\lambda_2 \end{align*} \]

发射端信号为 \(x(t)=x\cdot p(t)\cdot\beta\cos(2\pi f_c t)\) ，其能量为：

\[ E_s=\int_{-\infty}^{+\infty}x^2(t)\mathrm{d}t =\mathrm{E}(x^2)\beta^2\int_{-\infty}^{+\infty}\left[p(t)\cos(2\pi f_c t)\right]^2\mathrm{d}t \]

接收端：

\[ \begin{align*} y&=\int_{-\infty}^{+\infty}[x\cdot p(t)\cdot \beta\cos(2\pi f_c t)+z(t)]\cdot g(t)\cdot \gamma\cos(2\pi f_c t)\mathrm{d}t \\ &=x\int_{-\infty}^{+\infty}p(t)g(t)\cdot\beta\gamma\cos^2(2\pi f_c t)\mathrm{d}t+\int_{-\infty}^{+\infty}z(t)g(t)\cdot\gamma\cos(2\pi f_c t)\mathrm{d}t \\ &=x\int_{-\infty}^{+\infty}p(t)g(t)\cdot\beta\gamma\cos^2(2\pi f_c t)\mathrm{d}t+z \end{align*} \]

等效的电平噪声 \(z\) 满足：

\[ \mathbb{E}(z^2)=\frac{n_0}{2}\int_{-\infty}^{+\infty}\left( g(t) \gamma\cos(2\pi f_c t) \right)^2 \mathrm{d}t \]

（1） \(p(t),g(t)\) 为时域有限的矩形波，在区间 \(\mathbb{I}\{0\leqslant t<T\}\) 内，且 \(f_cT\in\mathbb{N}^+\) ，我们把积分上下限变到 \([0,T]\) ，则该区间内 \(p(t),g(t)\) 就是常数了，可以直接分离出来，积分很容易计算：

\[ \begin{align*} E_s &=\mathbb{E}(x^2)\beta^2\int_{-\infty}^{+\infty}\left[p(t)\cos(2\pi f_c t)\right]^2\mathrm{d}t \\ &=\mathbb{E}(x^2)\beta^2 \int_{0}^{T}\left[p(t)\cos(2\pi f_c t)\right]^2\mathrm{d}t\\ &=\mathbb{E}(x^2)\beta^2 \lambda_1 \int_{0}^{T}\cos^2(2\pi f_c t)\mathrm{d}t \\ &=\mathbb{E}(x^2)\left(\lambda_1\beta^2\frac{T}{2}\right) \end{align*} \]

同理可以得到：

\[ \mathbb{E}(z^2)=\frac{n_0}{2}\left( \lambda_2\gamma^2\frac{T}{2} \right),\quad z\sim\mathcal{N}\left(0,\frac{n_0}{2}\cdot \lambda_2\gamma^2\frac{T}{2}\right) \]

等效电平信道：

\[ y=x\left(\sqrt{\lambda_1 \lambda_2}\beta\gamma \frac{T}{2}\right)+z \]

接收端波形能量为：

\[ \mathbb{E}(x^2)\left(\int_{-\infty}^{+\infty}\left( p(t)g(t)\beta \gamma\cos^2(2\pi f_c t) \right)^2 \mathrm{d}t \right)^2=\mathbb{E}(x^2)\left(\lambda_1 \lambda_2 \beta^2 \gamma^2 \frac{T^2}{4}\right) \]

因此接收端的信噪比为：

\[ \mathrm{SNR}=\frac{\mathbb{E}(x^2)\left(\lambda_1 \lambda_2 \beta^2 \gamma^2 \dfrac{T^2}{4}\right)}{\dfrac{n_0}{2}\cdot \lambda_2\gamma^2\dfrac{T}{2}}=\frac{\mathbb{E}(x^2)}{n_0/2}\cdot \left(\lambda_1 \beta^2 \frac{T}{2}\right) \]

假设发送符号 \(x\) 均匀分布，间距为 \(2A\) ，则接收端的电平到判决门限的距离、等效噪声标准差变为：

\[ A'=A\cdot\left(\sqrt{\lambda_1 \lambda_2}\beta\gamma \frac{T}{2}\right),\quad \sigma'=\sqrt{\frac{n_0}{2}\cdot \lambda_2\gamma^2\frac{T}{2}} \]

其实就相当于先对 \(p(t),g(t)=\lambda p(-t)\) 进行归一化，然后将多出来的系数加到载波上 \(\beta\to \beta',\;\gamma\to\gamma'\) . 之后的分析与前面的讨论矩形包络载波传输相同。

（2）\(p(t),g(t)\) 为时域无限、频域有限的波，带限为 \(|f|\leqslant W\) ，且载频 \(f_c>W\) ，利用载波的频谱搬移特性，我们仍然可以求解积分：

\[ \begin{align*} E_s &=\mathbb{E}(x^2)\beta^2\int_{-\infty}^{+\infty}\left[p(t)\cos(2\pi f_c t)\right]^2\mathrm{d}t \\ &=\mathbb{E}(x^2)\beta^2\int_{-\infty}^{+\infty}p^2(t)\cos^2(2\pi f_c t)\mathrm{d}t \\ &=\mathbb{E}(x^2)\beta^2\int_{-\infty}^{+\infty}p^2(t)\frac{1+\cos(4\pi f_c t)}{2}\mathrm{d}t \\ &=\mathbb{E}(x^2)\beta^2\int_{-\infty}^{+\infty}p^2(t)\frac{1}{2}\left(1+\frac{1}{2}e^{\mathrm{j}4\pi f_c t}+\frac{1}{2}e^{-\mathrm{j}4\pi f_c t}\right)\mathrm{d}t \\ &=\mathbb{E}(x^2)\beta^2\left(\frac{\lambda_1}{2}+\frac{1}{2}\int_{-\infty}^{+\infty}p^2(t)e^{\mathrm{j}4\pi f_c t}\mathrm{d}t+\frac{1}{2}\int_{-\infty}^{+\infty}p^2(t)e^{-\mathrm{j}4\pi f_c t}\mathrm{d}t\right) \\ &=\mathbb{E}(x^2)\beta^2\left(\frac{\lambda_1}{2}+\frac{1}{2}\mathcal{F}[p^2(t)](f)\big|_{f=2f_c}+\frac{1}{2}\mathcal{F}[p^2(t)](g)\big|_{f=-2f_c} \right) \\ \end{align*} \]

根据傅里叶变换“时域相乘，频域卷积”的性质，有 \(\mathcal{F}[p^2(t)](f)=P(f)*P(f)\) . 由于 \(P(f)\) 是基带频谱 \(-W\sim W\) 的信号，经过卷积后 \(P(f)*P(f)\) 为频谱范围 \(-2W\sim 2W\) 的信号。然而我们有条件 \(f_c>W \Rightarrow 2f_c>2W\) ，因此 \(f=\pm 2f_c\notin [-2W,2W]\) ，不在 \(P(f)*P(f)\) 频谱范围内，自然有 \(\mathcal{F}[p^2(t)](2 f_c)=\mathcal{F}[p^2(t)](-2 f_c)=0\) . 因此我们得到：

\[ E_s=\mathbb{E}(x^2)\left(\frac{1}{2}\lambda_1\beta^2\right) \]

这也就是为什么我们在设计带限载波传输方案的时候说过：

带宽 \(W\) 的理想低通对 \(P^*(f)\) 无影响，或者说 \(P^*(f)\) 本身就带限，相当于一个低通滤波器，也能成功滤掉 \(\pm 2f_c\) 处的高频分量。

同理可以得到：

\[ \mathbb{E}(z^2)=\frac{n_0}{2}\left(\frac{1}{2} \lambda_2\gamma^2 \right),\quad z\sim\mathcal{N}\left(0,\frac{n_0}{2}\cdot \frac{1}{2}\lambda_2\gamma^2\right) \]

等效电平信道：

\[ y=x\left(\frac{1}{2}\beta\gamma \sqrt{\lambda_1 \lambda_2}\right)+z \]

接收端波形能量为：

\[ \mathbb{E}(x^2)\left(\int_{-\infty}^{+\infty}\left( p(t)g(t)\beta \gamma\cos^2(2\pi f_c t) \right)^2 \mathrm{d}t \right)^2=\mathbb{E}(x^2)\left(\frac{1}{4}\lambda_1 \lambda_2 \beta^2 \gamma^2\right) \]

因此接收端的信噪比为：

\[ \mathrm{SNR}=\frac{\mathbb{E}(x^2)\left(\dfrac{1}{4}\lambda_1 \lambda_2 \beta^2 \gamma^2 \right)}{\dfrac{n_0}{2}\cdot \dfrac{1}{2}\lambda_2\gamma^2}=\frac{\mathbb{E}(x^2)}{n_0/2}\cdot \left( \frac{1}{2}\lambda_1 \beta^2\right) \]

假设发送符号 \(x\) 均匀分布，间距为 \(2A\) ，则接收端的电平到判决门限的距离、等效噪声标准差变为：

\[ A'=A\cdot\left(\frac{1}{2}\beta\gamma \sqrt{\lambda_1 \lambda_2}\right),\quad \sigma'=\sqrt{\frac{n_0}{2}\cdot\frac{1}{2} \lambda_2\gamma^2} \]

附录 2¶

We can understand the principles of I/Q signals from another perspective.

In the real physical world, we can only transmit real-valued waveforms, like voltage or current. But we can use a complex number to represent the signal in order to simplify the analysis. We separate two mutually orthogonal components riding on the same carrier:

I (In-phase) — multiplied by the \(\cos()\) carrier.
Q (Quadrature) — multiplied by the \(\sin()\) carrier.

The transmitted signal becomes:

\[ x(t)=I(t)\cos(2\pi f_c t)-Q(t)\sin(2\pi f_c t) \]

It is equivalent to:

\[ x(t)=\mathcal{R}\{\left[I(t)+\mathrm{j}Q(t)\right]\mathrm{e}^{\mathrm{j}2\pi f_c t}\} \]

so that the signal can be condensed into the complex envelope \(I+\mathrm{j}Q\) .

波形信道¶

波形信道概述¶

加型高斯白噪声信道¶

最佳接收（匹配滤波）¶

实电平波形传输最佳接收¶

收发联合模型¶

无失真传输准则¶

升余弦滤波系统¶

数字基带传输¶

矩形包络载波传输¶

二进制单路载波传输¶

多进制单路载波传输¶

I,Q 路载波传输¶

带限载波传输¶

单路带限载波传输¶

I,Q 路带限载波传输¶

基带信号功率谱¶

载波信号功率谱¶

数字调制总结¶

附录 1¶

附录 2¶

Comments