差错控制¶

Abstract

重点掌握： 1. 了解和对比三种典型差错控制体制。 2. 由最小码距计算纠错位数和检错位数。 3. 会用典型检错算法进行检错判断，并针对停等 ARQ，分析其吞吐量和差错概率。 4. 选择重传的吞吐量和差错分析，回溯 N 重传的机制和循环冗余校验（CRC）。 5. 给定生成矩阵，计算校验矩阵，并做编、译码的输入、输出计算。 6. 给定部分码本，计算线性系统码的生成矩阵。 7. 汉明码的构造方法，编译码计算和性能分析。 8. 给定突发差错的位数，设计交织器参数。

差错控制的主要方法：

（1）反馈原信息进行确认

Destination 把从 Source 处收到的 bit 串原样发送给 Source，然后由 Source 来判断：若与所发一致，则发送下一个 bit 串，否则重发这一组 bit 串。

不一定绝对可靠（因为反馈过程中也可能出错），且效率太低。

（2）检错重发（Automatic Repeat Request, ARQ）

Source 对准备发送的 bit 串添加冗余位，用于检错。只要有一个 bit 位不对，就需要重发。

降低了通信效率和速率。

例如，我们原本仅仅发送 1 个 bit：“0” 或 1，现在添加 2 个 bit 的冗余位：

\[ \begin{cases} 0 \to 000 \\ 1 \to 111 \end{cases} \]

接收端判断： \(000\to 0,\; 111\to 1\) ，其余 6 中情况 \(110,101,001,\cdots\) 全部判错，需要重发。该过程为纯检错。

（3）前向纠错（Forward Error Correction, FEC）

有一些通信系统没有反馈链路（例如电视），或者无法容忍重传的延时，因此 ARQ 方法不适用。而 FEC 的方案是“相信大多数”，Destination 对接收到的 bit 串进行纠错。

例如，我们原本仅仅发送 1 个 bit：“0” 或 1，现在添加 2 个 bit 的冗余位：

\[ \begin{cases} 0 \to 000 \\ 1 \to 111 \end{cases} \]

接收端判断：

\[ \begin{cases} 000,001,010,100 \to 0 \\ 111,110,101,011 \to 1 \end{cases} \]

我们容忍可能出现的错误，最邻近码字原则（nearest neighbor decoding）进行判断：对于 \(111\) ，只要接收的 3 位 bit 串中有 2 位与它相同，就认为发送的是 \(111\) . 该过程为纯纠错。

码本的检错与纠错¶

检错：检查收到的数据是否发生错误，但不修改数据，只是报告“对/错”。只能分成“合法码字”和“非法码字”两个集合，非法的就丢掉重传。

纠错：不仅能发现错误，还能推断出原始数据并直接修正。收到非法码字后，能定位到它最可能的合法码字，然后替换成它。

定义：信息 bit 串映射的结果，称为码字；码字的集合，称码字集合；码字集合连同映射关系，称为码本。

两个 bit 串（或码字）对应位之间相异的 bit 个数称为汉明距离（Hamming Distance）

合法码字集合中，任意两个码字之间的汉明距离的最小值，称为最小汉明距离 \(d_{\min}=\displaystyle\min_{i,j} (\mathbf{c}_i,\mathbf{c}_j)\) .

沿用上述的例子，传输 \(0\to 000,\;1\to 111\) .

对于 ARQ，除了 \(000,111\) 这两种正确的，其余 6 种 \(110,101,011,100,010,001\) 都认为有错，称为检 2 位错。因此对于 \(000\) ，只要错误 bit 数不超过 2，就会变成非法码字，但是如果错 3 位，就会变成另外一个合法码字 \(111\) ，检不出来，因此最多能检 2 位错。
对于 FEC，收到 \(111,110,101,011\) 就认为是 \(111\to 1\) ，收到 \(000,001,010,100\) 就认为是 \(000\to 0\) ，称为纠 1 位错。因为对于 \(000\) ，如果错误 bit 数不超过 1 位，能够纠正回合法码字，例如 \(001\to 000\) ，但是如果错误 bit 位数超过 1 位，例如 \(011\to 111\) 会被纠成另外一个合法码字，因此最多纠 1 位错。

定理：给定码本，其纠错位数 \(t\) 和检错位数 \(e\) 满足 \(t+e+1\leqslant d_{\min}\) .

推论：\(2t+1\leqslant d_{\min},\quad e+1\leqslant d_{\min}\) .

同样可以分情况讨论：

全检错。只要不全错，就能检出原始 bit 串，因此 \(e=d-1\) . 无法纠错，因此 \(t=0\) .
全纠错。在 bit 码空间中，距离 \(00\cdots 0\) 较近的判为全 0，距离 \(11\cdots 1\) 较近的判为全 1 。若 \(d\) 为奇数，则 \(2t+1=d\) ，若 \(d\) 为偶数，则 \(2t+2=d\) ，综合起来就是 \(t=\left\lfloor\dfrac{d-1}{2}\right\rfloor,\;e=t\) ，即检出错误都能纠正。
既检错又纠错。在 bit 码空间中，在两个半径为 \(t\) 的圆之外，均为无法纠错的野生 bit 串，圆之内的能够纠错，因此 \(t+e+1=d\) .

检错算法¶

Note

本课程差错控制编译码的代数运算均在 \(GF(2)\) 上。

加法为异或运算 XOR \(\oplus:\;0+0=0,\;0+1= 1+0=1,\;1+1=0\) .

乘法： \(0\cdot 0=0,\;0\cdot 1=1\cdot 0=0,\; 1\cdot 1=1\) .

\(GF(2)\) 上也可以定义矢量，矩阵的运算，数的运算法则同上。运算的对应位置，可交换性等，同 \(\mathbb{R}\) 上的矢量矩阵运算。

奇偶位校验。把原 bit 串各位相加得到的结果，添加到原 bit 串后面。

设原 bit 串为 \(\mathbf{m}=[m_1m_2\cdots m_k]\) ，则编码方式为 \(\mathbf{c}=[c_1c_2\cdots c_{k+1}]\) ：

\[ c_i=\begin{cases} m_i, & i=1,2,\cdots,k \\ \displaystyle\sum_{j=1}^k m_j, & i=k+1 \end{cases} \]

写为矩阵形式：

\[ \mathbf{c}=\mathbf{m}\begin{pmatrix} 1 & 0 & \cdots & 0 & 1 \\ 0 & 1 & \cdots & 0 & 1 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 1 & 1 \\ \end{pmatrix}=\mathbf{m}[\mathbf{I}_{k\times k} \mid \mathbf{1}_{k\times 1}],\quad \mathbf{c}\in\mathbb{R}^{1\times (k+1)},\;\mathbf{m}\in\mathbb{R}^{1\times k} \]

解码方式：注意到

\[ \begin{align*} \sum_{i=1}^{k+1} c_i &= m_1 + m_2 + \cdots + m_k + \sum_{j=1}^{k} m_j \\ &= (m_1 + m_1) + (m_2 + m_2) + \cdots + (m_k + m_k) \\ &= 0 + 0 + \cdots + 0 \\ &= 0 \end{align*} \]

故当 \(\displaystyle \sum_{i=1}^{k+1} c_i = 0\) 或 \(\mathbf{c} \cdot \mathbf{1}_{k\times 1} = 0\) 时，判为无错，否则报错，请求重发。

奇偶校验的检错能力： \(e = 1,\;t = 0\) . 即检 1 位错，无法纠错。

原因：

当 \(\mathbf{c}\) 中错 2 个 bit 及任意偶数个 bit 时 \(\mathbf{c}\cdot \mathbf{1}_{k\times 1}\) 仍为 0，无法检错。因此最多检 1 位错。
如果某个码字发生 1 位错误，我们知道“出错了”，但不能判断它原来是哪个合法码字。因为距离它 1 位的合法码字有很多个，没有“唯一最近”的合法码字可选。因此无法纠错。

性质：\(d_{\min} = 2\)，因为对于 \(\mathbf{c}\) 翻转其中任意 2 个 bit 后得到的 \(\mathbf{c}'\) 仍满足 \(\mathbf{c}'\cdot \mathbf{1}_{k\times 1} = 0\) ，说明 \(\mathbf{c}'\) 也是合法码字，故 \(d(\mathbf{c}, \mathbf{c}') = 2\) .

漏检概率 \(p_m\) 为一个检错码发生差错，但未能检出的概率。对奇偶校验码，该漏检可能的情况为“错误偶数个 bit”，假设单个 bit 的差错概率为误 bit 率 \(P_b\) ，则：

\[ \begin{align*} p_m &= \binom{k+1}{2} P_b^2(1 - P_b)^{k-1} + \binom{k+1}{4} P_b^4(1 - P_b)^{k-3} + \cdots + \binom{k+1}{\left\lfloor \frac{k+1}{2} \right\rfloor} P_b^{2\left\lfloor \frac{k+1}{2} \right\rfloor}(1 - P_b)^{k+1-2\left\lfloor \frac{k+1}{2} \right\rfloor} \\ &= \sum_{i=1}^{\left\lfloor \frac{k+1}{2} \right\rfloor} \binom{k+1}{2i} P_b^{2i}(1 - P_b)^{k+1-2i} \end{align*} \]

停-等重传机制¶

码字： \(k\) 个信息 bit，映射（编码）成 \(n\) 个编码后的 bit（码字长度，对奇偶校验码 \(n=k+1\) ）。

\(T_m\)：传输一个码字的时间（传完才能译码）， \(T_m = \dfrac{n}{R_b}\) .

\(T_d\)：传播延时（对无线电有 \(T_d\) = 传播距离 / 光速）。

\(T_c\)：译码的计算时间。

\(T_a\)：传输一个 ACK/NACK 的时间， \(T_a = \dfrac{\text{ACK/NACK 的比特计数}}{R_b}\) .

我们感兴趣停等 ARQ 的效率，在一个轮次中真正用于传输码字（注意，还不是消息 bit）的时间为 \(T_m\) ，额外的时间开销为：

\[ T_{dca} = 2T_d + T_c + T_a \]

即使一轮传输成功（无错，或有错但检不出来）其效率（有效码字传输时间在一轮中的占比）为：

\[ \xi' = \frac{T_m}{T_m + T_{dca}} \]

成功（ACK）概率为 \(p_{suc} = \left(\dfrac{1 - P_b}{n}\right)^n + p_m\) ，不成功（NACK）概率为 \(1 - p_{suc}\) .

在第 \(i\) 轮成功的概率为 \(\left(\dfrac{1 - p_{suc}}{i - 1}\right)^{i - 1} p_{suc}\) ，服从几何分布。

要收到 ACK 的平均轮次数即为几何分布的期望 \(\dfrac{1}{p_{suc}}\) . 因此，要收到 ACK 需等待的时间为 \(\dfrac{T_m+T_{dca}}{p_{suc}}\) .

考虑随机误码引起重传，其效率为 \(\xi = \xi' p_{suc} = \dfrac{T_m p_{suc}}{T_m + T_{dca}}\) .

最后，注意到码字的 \(n\) 个 bit 中只有 \(k\) 个信息（消息）bit，故上层数据 bit 流体验到的速率为

\[ r = \frac{k}{n} \xi R_b = \frac{k p_{suc}}{n} \cdot \frac{T_m R_b}{T_m + T_{dca}} = \frac{k \left[(1 - P_b)^n + p_m\right]}{n} \cdot \frac{T_m R_b}{T_m + T_{dca}} \]

线性系统码¶

除检错重发之外，前向纠错是另一大类典型差错控制方案，其通过纠错码（又称信道编码）实现，分为分组码与非分组码两大类。

纠错码：

分组码：从上层信息流中，每次切出 \(k\) 个（与信息流其它 bit 无关的）消息 bit 作为一个分组，即 \(\mathbf{m}\) ，映射为 \(n\) 个编码 bit 即码字 \(\mathbf{c}\) ，译码时只看 \(\mathbf{c}\) 经过 BSC 之后的 \(n\) 个 bit。
1. 线性分组码：若一分组码中，任意两个合法（许用）码字 \(\mathbf{c}_1\) 和 \(\mathbf{c}_2\)，其线性组合 \(\mathbf{c}_1 + \mathbf{c}_2\)（ \(GF_2\) 上只有这一种组合方式）仍为合法码字。
  1. 线性系统码：若一线性分组码，对于 \(\forall\) 消息 \(\mathbf{m}\)，其对应的编码结果满足 \(c_i = m_i,\; i = 1, 2, \cdots, k\) ，也就是编码结果的前半部分包含原始的 bit 串分组。
  2. 线性非系统码。
2. 非线性分组码：例如 LDPC，Polar 码等。
非分组码：有卷积码（整个信息流与某 bit 串做“卷积”，无法分组），Turbo 码（卷积码+ 交织器）。

对于分组码：定义 \((n, k)\) 分组码，相当于从 \(GF_2\) 上的低维空间 \(k\) 维向高维空间 \(n\) 维的映射。消息 bit 任意组合，故 \(m\) 有 \(2^k\) 个，遍布 \(GF_2^k\) 中每个点，最小汉明距离为 1。

合法（许用）码字 \(\mathbf{c}\) 与 \(\mathbf{m}\) 一一对应，故只有 \(2^k\) 个，而 \(GF_2^n\) 中有 \(2^n\) 个点，故 \(\mathbf{c}\) 的分布相对稀疏，提升了最小汉明距，提供了纠错能力。

代价是，在保持有用信息传输速率不变时，要求信道提供的 bit 速率提升为 \(\dfrac{n}{k} \tilde{R}_b\) ，可用的每 bit 能量降为 \(\frac{k}{n} E_b\) . 其中 \(\tilde{R}_b\) 为单位时间内需传输的信源 bit 数， \(E_b\) 为每个信源 bit 可用的能量。对信源而言，其速率只能是信道速率 \(\tilde{R}_b\) 的 \(\frac{k}{n}\) 倍。

对于线性分组码，总存在一个 \(k \times n\) 维矩阵 \(\mathbf{G}\)，可将从 \(\mathbf{m}\) 到 \(\mathbf{c}\) 的映射表示为：

\[ \mathbf{c}=\mathbf{m}\mathbf{G} \]

\(\mathbf{G}\) 又称为该 \((n, k)\) 线性分组码的生成矩阵。

进一步地，对于线性系统码，其生成矩阵 \(\mathbf{G}\) 需满足如下形式:

\[ \mathbf{G}_{k \times n} = \left[ \mathbf{I}_{k \times k} \mid \mathbf{P}_{k \times (n-k)} \right] \]

此时：

\[ \mathbf{c} = \mathbf{m} \mathbf{G} = \left[ \mathbf{m} \mid \mathbf{m} \mathbf{P} \right] \]

其中 \(\mathbf{m}\) 为 \(k\) 位信息位（Message bits）， \(\mathbf{mP}\) 为 \((n - k)\) 位校验位（Parity bits）。

那么如何判断一个 \(n\) 位 bit 串是否为合法码字？

根据 \(GF_2\) 空间上的运算特性：

\[ \begin{gather*} [\mathbf{I}\mid \mathbf{P}] \begin{bmatrix} \mathbf{P} \\ \mathbf{I} \end{bmatrix} = \mathbf{I}_{k \times k} \mathbf{P}_{k \times (n-k)} + \mathbf{P}_{k \times (n-k)} \mathbf{I}_{(n-k) \times (n-k)} = \mathbf{0} \\ \forall \mathbf{m}, \quad \mathbf{m} [\mathbf{I}\mid \mathbf{P}] \begin{bmatrix} \mathbf{P} \\ \mathbf{I} \end{bmatrix} = \mathbf{m} \cdot \mathbf{0} = \mathbf{0} \end{gather*} \]

若记 \(\mathbf{H}^T = \begin{bmatrix} \mathbf{P} \\ \mathbf{I} \end{bmatrix}\in\mathbb{R}^{n\times(n-k)}\) ，称 \(\mathbf{H}\) 为校验矩阵，则合法码字 \(\mathbf{c}\) 一定满足 \(\mathbf{c} \mathbf{H}^T = \mathbf{0}\) ，也即合法码字空间为 \(\mathbf{H}^T\) 的左零空间。

具体求解 \(\mathbf{G},\mathbf{H}^T\) ，以及计算 bit 串编码输出、根据接收到的码字判断是否为合法码字的时候，核心方法是高斯消元法。

分组码译码¶

分组码传输的噪声模型：

\[ \begin{matrix} & \mathbf{e} & \\ & \downarrow & \\ \mathbf{x} \longrightarrow & \oplus & \longrightarrow \mathbf{y}=\mathbf{x}+\mathbf{e} \end{matrix} \]

其中 \(+\) 运算为异或运算，噪声矢量 \(\mathbf{e}=[e_1,e_2,\cdots,e_n]\) 各分量独立同分布 \(e_i\overset{i.i.d.}{\sim}\begin{pmatrix} 0 & 1\\ 1-P_b & P_b \end{pmatrix}\) .

由于 MAP 准则在假设检验（统计学）上普适最优，当然也适用于分组码译码。再由 \(m\) 均匀分布，概率均为 \(2^{-k}\) ，故 \(\mathbf{x}\) 等概，于是 ML 准则适用。即：

\[ \hat{\mathbf{x}} = \arg\max_{\mathbf{x} \in \mathcal{C}} \Pr\{\mathbf{y}|\mathbf{x}\} \]

引理：对于 \(P_b < 0.5\) 的 BSC 信道，ML 准则等价于最小汉明距离准则，即：

\[ \hat{\mathbf{x}} = \arg\min_{\mathbf{x} \in \mathcal{C}} d_H(\mathbf{x}, \mathbf{y}) \]

汉明码¶

首先，我们要做一个假设，即 \(\mathbf{e}\) 中最多只有一个 “1”，其余全是 “0”，最多纠一位错。因此 \(\mathbf{e} = \mathbf{0}\) 或 \(\mathbf{e} = [0, \cdots, 0, 1, 0, \cdots, 0]\) 第 \(i\) 位为 “1”，其余为 “0”。

由线性码性质 \(\mathbf{G} \mathbf{H}^T = \mathbf{0} \Rightarrow \mathbf{m} \mathbf{G} \mathbf{H}^T =\mathbf{c}\mathbf{H}^T= \mathbf{0}\) ，而 \(\mathbf{x} \in \{\mathbf{c} : \mathbf{c} \in \mathcal{C}\}\) ，因此：

\[ \mathbf{y} \mathbf{H}^T = (\mathbf{x} + \mathbf{e}) \mathbf{H}^T = \mathbf{x} \mathbf{H}^T + \mathbf{e} \mathbf{H}^T = \mathbf{e} \mathbf{H}^T = \mathbf{0} \]

设 \(\mathbf{s}=\mathbf{y}\mathbf{H}^T\) 为校正子，因此 \(\mathbf{s}=\mathbf{e}\mathbf{H}^T\) .

若无错，则 \(\mathbf{s}=\mathbf{e}=0\) .
若有错且出错在第 \(i\) 位，即 \(e_i=1\) ，其余为 \(0\) ，则 \(\mathbf{s}=\mathbf{H}^T(i,:)\) 为 \(\mathbf{H}^T\) 的第 \(i\) 行，经过对比就能知道是哪一位出错了。

同时，上面的要求也对 \(\mathbf{H}^T\) 提出了约束：

\(\mathbf{H}^T\) 的 \(n\) 个行各不相同。
\(\mathbf{H}^T\) 中不能有全 0 的行。

由于 \(\mathbf{H}^T\) 是 \(GF_2\) 上的 \(n \times (n-k)\) 维矩阵，故每行是 \((n-k)\) 维行矢量，共有 \(2^{n-k}\) 个，排除一个全 0 矢量，共有 \(2^{n-k} - 1\) 个。

用 \(2^{n-k} - 1\) 个非零行矢量标识 \(n\) 位可能的差错（ \(\mathbf{e}\) 中 “1” 可能的位置），必须一一对应，故有：

\[ 2^{n-k} - 1 = n \quad \Longleftrightarrow \quad n + 1 = 2^{n-k},\quad \begin{cases} n = 2^m - 1 \\ k = 2^m - m - 1 \end{cases} \]

其中 \((n-k)\) 为校验位个数，也记为 \(m\) ，需从正整数中选取典型值，例如下表：

\(m = n - k\)	\((n, k)\) 线性码
2	(3,1)
3	(7,4)
4	(15,11)
5	(31,26)

定理：定理：\((n, k)\) 汉明码的 \(d_H^{\min} = 3\) ，纠错位数 \(t=1\) ，用满了码距。

典型题型 1：给定信源的消息 bit 速率 \(R_b\) ，求用 \((n, k)\) 码编码后，滚降系数 \(\alpha\) 和许用电平数 \(M\) .

解题关键：编码后需传输的 bit 速率提升到 \(\dfrac{n}{k} R_b\) .

典型题型 2：给定 \(P_b\) ，求 \((n, k)\) 汉明码纠错失败的概率 \(P_e\) 即 \(\Pr\{\hat{\mathbf{c}} \neq \mathbf{c}\}\) ，又称误块率。

解题关键： \((n, k)\) 汉明码可纠一位错。故 \(\{\text{成功纠错}\} = \{\text{无错}\} \cup \{n \text{ 位中错一位}\}\) ，因此：

\[ P_e = 1 - (1 - P_b)^n - \binom{n}{1} P_b (1 - P_b)^{n-1} \]

有的题目中 \(P_b\) 还需从电平或波形信道的参数中算出来，若给定信源 bit 的每 bit 可用能量 \(E_b\) ，则传输时（编码后）每 bit 能量降为 \(\dfrac{k}{n}E_b\) .

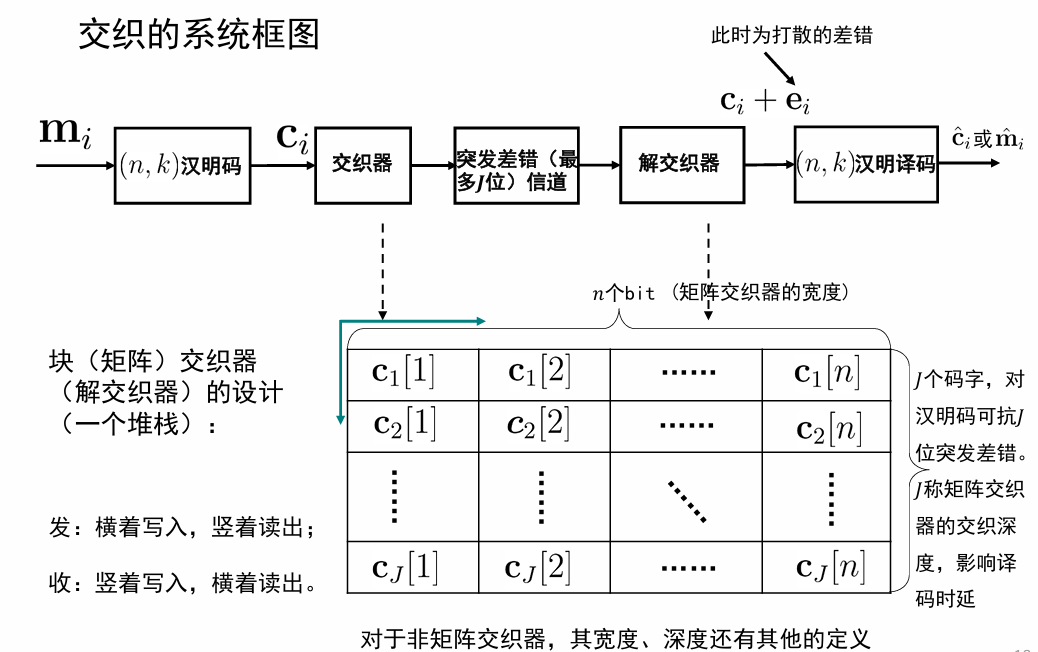
交织¶

汉明码适合纠“零星”错误，但对“集中突发”的误码无能为力。例如：在同样误码率下，要么不错，要错就连错 3 个 bit（无线通信常有此类情况）。此时汉明码毫无作用，甚至越纠越错。