Linear Kalman Filter¶

卡尔曼滤波不同于传统的具有频域选频特性的滤波器，它是一种时域滤波器，更准取地说它是一种最优估计方法，可以根据已知的先验知识，预测下一个时刻的估计值。

滤波的本质是加权，对应到卡尔曼滤波中，这个权重由卡尔曼增益决定，它融合的数据有两个：满足一定分布的先验状态估计值、满足一定分布的观测值。

本节讨论的是线性卡尔曼滤波（Linear Kalman Filter, LKF），一般不加特殊说明时，卡尔曼滤波都是指线性卡尔曼滤波，也就是 KF = LKF。非线性的情况有其他的卡尔曼滤波变体，例如扩展卡尔曼滤波 EKF、无迹卡尔曼滤波 UKF 等。

The following content is referenced from: KalmanFilter.NET.

一维无过程噪声 KF¶

卡尔曼滤波的核心步骤是“测量、更新、预测”。它将测量值、当前状态估计和下一个状态预测都视为正态分布的随机变量。

对随机变量进行估计时，称估计值和真值之间的差为“估计误差”。随着时间不断增长，估计误差不断下降最终收敛到 0。实际中我们并不知道估计误差，因为真值是未知的，但是我们可以计算估计值的不确定性，也就是状态估计值的方差为 \(p\) .

对随机变量进行测量时，称测量值和真值之间的差为“测量误差”。测量误差是随机的，一般使用正态分布的方差 \(\sigma^2\) 描述，对应的标准差 \(\sigma\) 称为测量不确定性。记测量值的方差为 \(r\) . 最常见的是测量设备，比如雷达的测量的不确定性。

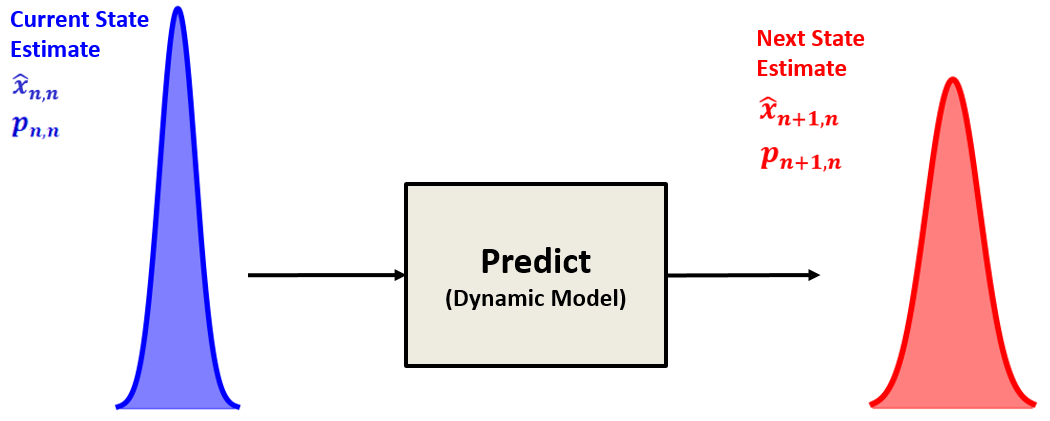
状态的预测。根据当前状态的估计值，结合我们建立的系统动态模型（例如匀速直线运动、匀加速直线运动），对下一个时刻的状态值进行预测。等到下一个时刻，这个预测值就是下一时刻的“先验估计”。

这个预测过程相当于一个“外插”。卡尔曼滤波将状态的估计视为一个随机变量，因此除了估计状态变量本身，还需要对它的方差/协方差进行估计。

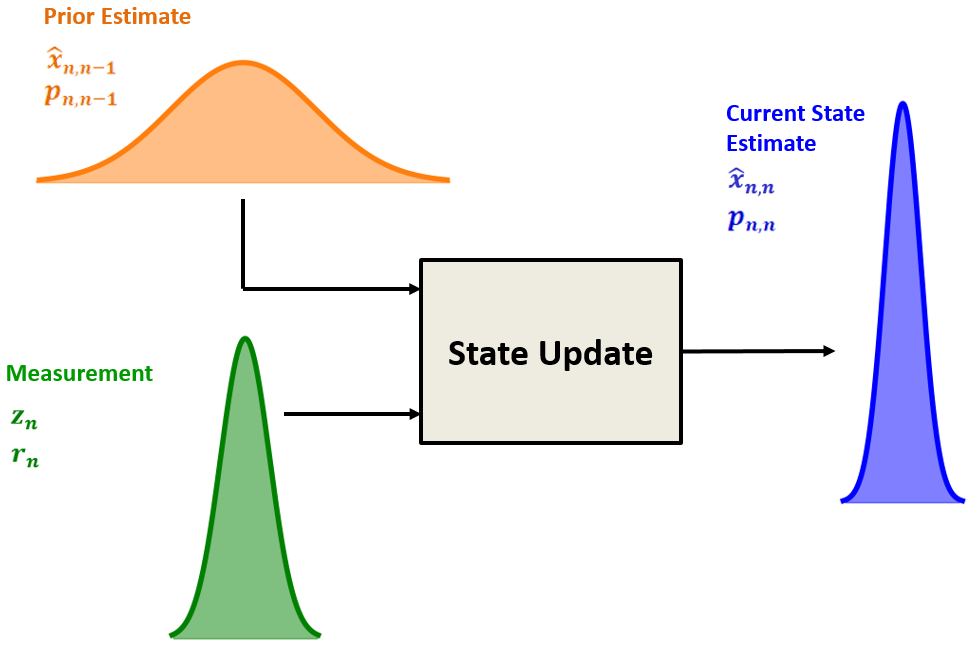
状态的更新。每一个时刻，我们使用当前的两个随机变量来估计当前系统的状态：上一个时刻对当前时刻的预测、当前时刻的测量值。卡尔曼滤波器是一种最优滤波器，最优性体现在它能够把上述状态预测和测量值融合在一起，使得得到的当前状态方差最小。

我们将状态估计值和写为状态预测值和测量值的加权和形式：

其中 \(p_{n|n}\) 即为最优估计 \(\hat x_{n|n}\) 的方差， \(r_n\) 为测量值 \(z_n\) 的方差。权重 \(\lambda>0\) 代表了状态估计值和测量值之间选择的偏好。例如如果使用的雷达精度较高，对应的 \(\lambda\) 应该较大，更倾向于相信雷达的测量值。

我们希望最小化状态估计值 \(\hat x_{n|n}\) 的方差 \(p_{n|n}\) ，因此对其求导：

因此最优估计的公式，也即卡尔曼增益方程为：

称这个权重 \(K_n\) 为卡尔曼增益，它也是一个随时间更新的变量。卡尔曼增益越高，越相信测量值，代表了有多少测量值进入到最终的估计值。

将 \(K_n\) 带入协方差更新公式：

得到协方差更新方程：

由方程可知 \(1-K_n<1\) ，状态估计的方差是始终随着滤波器迭代而下降。当测量不确定性很高时，卡尔曼增益很低，几乎只依赖状态预测值，因此状态估计不确定性收敛的速度会较慢；相反当测量不确定性很低时，卡尔曼增益很高，几乎只依赖测量值，因此状态估计不确定性会快速收敛到0。

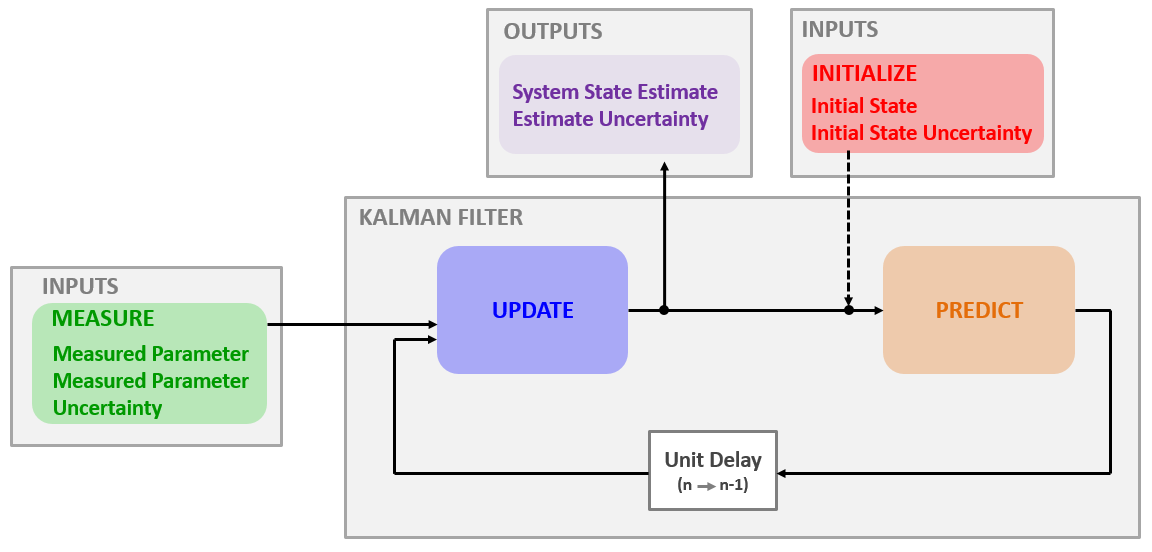
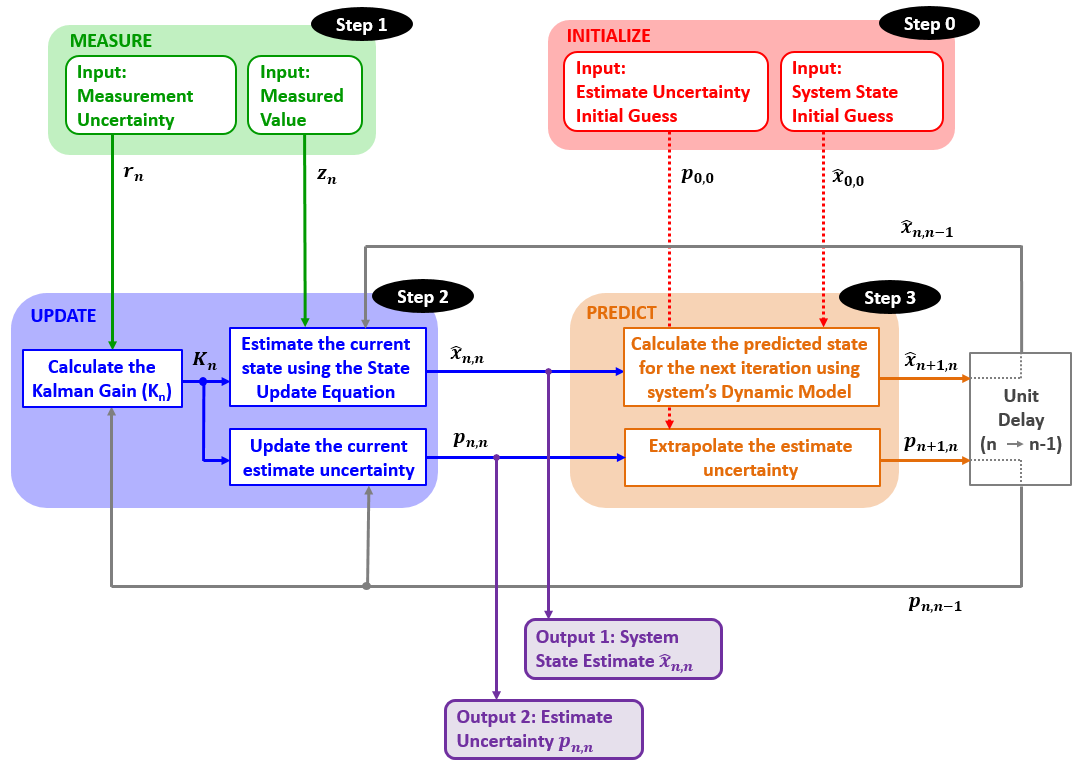
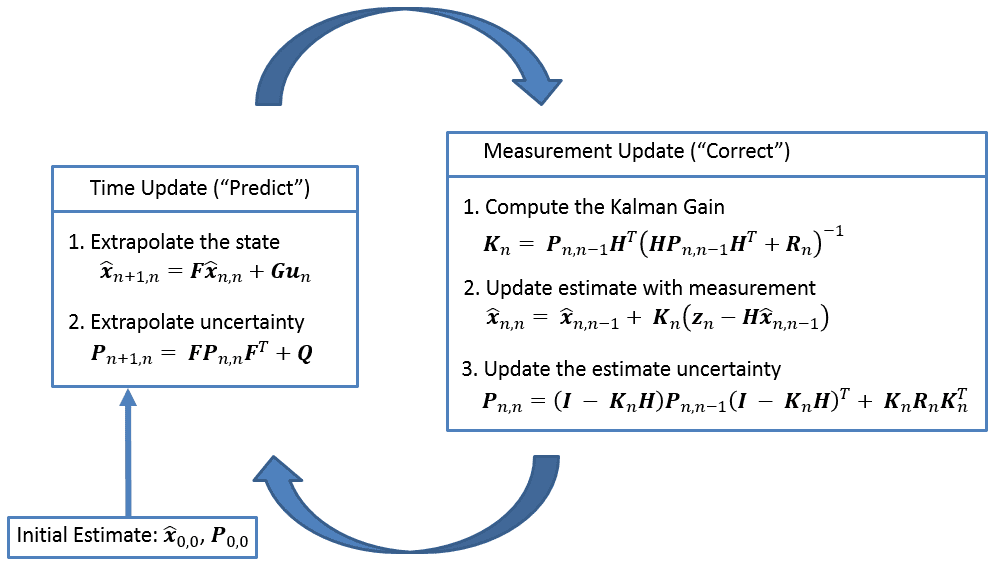
由此我们可以总结卡尔曼滤波的整体框架：

滤波器的输入为：

1. 初始化
   • 初始状态 \(\hat x_{0|0}\)
   • 初始状态方差 \(p_{0|0}\)

   • 初始化参数可以由其他的系统、过程（例如雷达的搜索模式）或基于经验和理论知识所得出的合理的猜测来获得。即使初始化参数不太准确，卡尔曼滤波器也能收敛到接近真值。

2. 测量

   • 每个滤波器采样周期都要进行测量。每次测量得到两个参数：

   • 测量值 \(z_n\)
   • 测量方差 \(r_n\)

滤波器的输出为：

• 状态估计 \(\hat x_{n|n}\)
• 状态估计方差 \(p_{n|n}\)

5个核心方程（以一维匀速运动为例）：

状态更新阶段：

• 卡尔曼增益 Kalman Gain： \(K_n=\dfrac{p_{n|n-1}}{p_{n|n-1}+r_n}\)
• 状态更新 State Update： \(\hat x_{n|n} =\hat x_{n|n-1} + K_n (z_n-\hat x_{n|n-1})\)
• 协方差更新 Covariance： \(p_{n|n}=(1-K_n)p_{n|n-1}\)

状态预测阶段：

• 状态转移/外插 Transition Equation： \(\hat x_{n|n-1}=\hat x_{n-1|n-1}+\hat v_{n-1|n-1}\Delta t,\quad\hat v_{n|n-1}=\hat v_{n-1|n-1}\)
• 协方差转移/外插： \(p_{n|n-1}^x=p_{n-1|n-1}^x+p_{n-1|n-1}^v \Delta t^2,\quad p_{n|n-1}^v=p_{n-1|n-1}^v\)

一维 KF¶

上述讨论的“一维无过程噪声 KF”中，我们没有考虑过程噪声。真实世界中，系统动力模型总是有不确定性的。比如我们想测量一个电阻的阻值，我们假设它是不变的，即阻值不随测量过程而改变，但实际上阻值会随着环境温度的改变而轻微改变。再比如用雷达追踪弹道导弹时，导弹动态模型的不确定性会包含一些随机的加减速。对于飞行器之类的目标，模型不确定性更大，因为飞行员随时可能进行机动。另一方面，当我们用 GPS 接收机计算一个固定物体的位置时，由于固定物体不会动，所以动态模型不确定性为 0。动态模型的不确定性称为过程噪声，也叫模型噪声、驱动噪声、动态噪声或系统噪声。过程噪声也会带来估计误差。

过程噪声的方差使用 \(q\) 表示。协方差外插方程中，还应该加上过程噪声的影响：

加入过程噪声后，完整的一维卡尔曼滤波方程为：

• 卡尔曼增益 Kalman Gain： \(K_n=\dfrac{p_{n|n-1}}{p_{n|n-1}+r_n}\)
• 状态更新 State Update： \(\hat x_{n|n} =\hat x_{n|n-1} + K_n (z_n-\hat x_{n|n-1})\)
• 协方差更新 Covariance： \(p_{n|n}=(1-K_n)p_{n|n-1}\)

状态预测阶段：

• 状态转移/外插 Transition Equation： \(\hat x_{n|n-1}=\hat x_{n-1|n-1}+\hat v_{n-1|n-1}\Delta t,\quad\hat v_{n|n-1}=\hat v_{n-1|n-1}\)
• 协方差转移/外插： \(p_{n|n-1}^x=p_{n-1|n-1}^x+p_{n-1|n-1}^v \Delta t^2,\quad p_{n|n-1}^v=p_{n-1|n-1}^v+q_{n-1}\)

多维 KF¶

现在我们将一维卡尔曼滤波扩展到多维卡尔曼滤波。例如在三维空间中，我们追踪一个目标的位置，可以考虑其坐标、速度、加速度等：

使用匀加速运动模型：

在卡尔曼滤波问题中，我们设定状态为 \(\boldsymbol{x}_n\) ，控制输入为 \(\boldsymbol{u}_n\) （可选），假设系统满足以下包含高斯白噪声的线性模型：

其中系统过程噪声 \(\boldsymbol{w}\) 和测量噪声 \(\boldsymbol{v}\) 均为高斯白噪声。

系统状态的真实值 \(\boldsymbol{x}\) 是一个确定值，但是我们无法得知真实值，而是对状态给出一个估计值 \(\hat{\boldsymbol{x}}\) （在已知观测数据时的后验估计），估计值和真实值之间的差异我们用高斯噪声描述估计值的不确定度，用协方差矩阵 \(\boldsymbol{P}\) 表示。我们可以认为估计值是真实值叠加噪声后的数据，具有一定的不确定度，但是在数学上我们更习惯反过来（将高斯噪声移到等号另一边仍为高斯噪声），将真实值描述为围绕估计值波动的随机变量，以描述我们的对真实值的未知性。因此，在 \(n\) 时刻，系统状态的估计为 \(\boldsymbol{x}_n\sim\mathcal{N}\left(\hat{\boldsymbol{x}}_{n|n},\boldsymbol{P}_{n|n}\right)\) .

状态外插方程¶

状态外插方程，用矩阵形式描述为：

其中：

• \(\hat{\boldsymbol{x}}_{n+1|n}:n_x\times 1\) 为 \(n\) 时刻对 \(n+1\) 时刻系统状态的预测。
• \(\hat{\boldsymbol{x}}_{n|n}\) 为 \(n\) 时刻对系统状态变量的估计。
• \(\boldsymbol{u}_n:n_u\times 1\) 为控制向量或输入向量，是系统的一个可测量的、确定性的输入。
• \(\boldsymbol{\omega}_n:n_x\times 1\) 为过程噪声，是影响系统状态的、不可测量的输入。
• \(\boldsymbol{F}:n_x\times n_x\) 为状态转移矩阵。
• \(\boldsymbol{G}:n_x\times n_u\) 为控制矩阵或输入转移矩阵，将控制量映射到状态变量上。

状态外插方程的推导需要使用到线性系统的状态空间：

求解微分方程，得到：

由此得到：

协方差外插方程¶

先给出协方差外插方程的一般形式：

其中：

• \(\boldsymbol{P}_{n+1|n}\) 为下一个状态预测时的协方差矩阵。
• \(\boldsymbol{P}_{n|n}\) 为当前状态估计的协方差矩阵。有 \(\boldsymbol{P}_{n|n}=\mathbb{E}(\boldsymbol{e}_n\boldsymbol{e}_n^T)=\mathbb{E}\left((\boldsymbol{x}_n-\hat{\boldsymbol{x}}_{n|n})(\boldsymbol{x}_n-\hat{\boldsymbol{x}}_{n|n})^T\right)\) .
• \(\boldsymbol{F}\) 为状态转移矩阵。
• \(\boldsymbol{Q}\) 为过程噪声协方差矩阵。有 \(\boldsymbol{Q}_n=\mathbb{E}(\boldsymbol{\omega}\boldsymbol{\omega}_n^T)\) .

简单的推导过程如下：

当不考虑过程噪声的时候， \(\boldsymbol{Q}=0\) . 根据协方差的定义：

根据状态外插方程 \(\hat{\boldsymbol{x}}_{n+1|n} = \boldsymbol{F} \hat{\boldsymbol{x}}_{n|n} + \boldsymbol{G} \hat{\boldsymbol{u}}_{n|n}\) 得到：

然后再添加上过程噪声 \(\boldsymbol{Q}\) 即可得到：

测量方程¶

测量值 \(z_n\) 代表系统的真实状态值和由测量设备引入的随机观测噪声 \(v_n\) 的叠加。

测量方程为：

其中：

• \(\boldsymbol{z}_n:n_z\times 1\) 为测量向量。
• \(\boldsymbol{x}_n\) 为系统真实状态，是隐藏的、未知的。
• \(\boldsymbol{v}_n:n_z\times 1\) 为测量的随机噪声向量。测量的协方差矩阵为 \(\boldsymbol{R}_n=\mathbb{E}(\boldsymbol{v}_n\boldsymbol{v}_n^T)\) .
• \(\boldsymbol{H}:n_z\times n_x\) 为观测矩阵。以线性变换的形式，将系统状态变换到测量的输出。这是因为实际中我们的测量设备不是直接获取系统的状态，而是间接的，例如一个电子秤，系统状态是质量，但是仪器本身测量的是电流。

状态更新方程¶

矩阵形式的状态更新方程：

其中：

• \(\hat{\boldsymbol{x}}_{n|n}\) 为 \(n\) 时刻对系统的状态估计。
• \(\hat{\boldsymbol{x}}_{n|n-1}\) 为在 \(n-1\) 时刻对 \(n\) 时刻系统的状态估计。
• \(\boldsymbol{K}_n:n_x\times n_z\) 为卡尔曼增益。

协方差更新方程¶

矩阵形式的协方差更新方程为：

其中：

• \(\boldsymbol{P}_{n|n}\) 为当前 \(n\) 时刻状态估计的协方差矩阵。
• \(\boldsymbol{P}_{n|n-1}\) 为前一时刻 \(n-1\) 时刻对当前 \(n\) 时刻状态预测的协方差矩阵。
• \(\boldsymbol{R}_n=\mathbb{E}(\boldsymbol{v}_n\boldsymbol{v}_n^T)\) 为测量噪声的协方差矩阵。
• \(\boldsymbol{I}\) 为维度 \(n_x\times n_x\) 的单位阵。

如下是一个简单的推导过程。我们将下面四个方程作为已知条件：

首先我们改写状态更新方程：

然后计算测量误差：

再求 \(\boldsymbol{P}_{n|n}\) ：

上式展开后有4项，观察中间2项，由于 \(\boldsymbol{x}_n-\hat{\boldsymbol{x}}_{n|n}\) 是先验估计的误差，它和当前时刻的测量噪声 \(\boldsymbol{v}_n\) 无关，两个不相关的随机变量的积的期望是0：

上式化简为：

卡尔曼增益¶

矩阵形式的卡尔曼增益公式为：

推导过程：重写协方差更新方程：

我们令 \(\boldsymbol{S}_n=\boldsymbol{H} \boldsymbol{P}_{n|n-1} \boldsymbol{H}^T + \boldsymbol{R}_n\) ，由于卡尔曼增益需要满足最小化估计值的方差，也就是协方差矩阵的主对角线上的值。我们选择的评判标准是“误差均方和”，也就是协方差矩阵的迹 \(\operatorname{tr}(\boldsymbol{P}_{n|n})\) . 利用恒等式 \(\operatorname{tr}(AB)=\operatorname{tr}(BA)\) ，我们有：

需要最小化迹 \(\operatorname{tr}(\boldsymbol{P}_{n|n})\) ，将其对卡尔曼增益 \(\boldsymbol{K}_n\) 求导，利用公式： \(\dfrac{\partial}{\partial K}\operatorname{tr}(A^TK)=A,\;\dfrac{\partial}{\partial K}\operatorname{tr}(KSK^T)=K(S+S^T)\) ，而显然 \(\boldsymbol{S}_n=\boldsymbol{S}_n^T\) ，因此：

由此可以得到卡尔曼增益方程：

事实上这里需要一个条件： \(\boldsymbol{S}_n\) 是正定的，即 \(\boldsymbol{S}_n\succ 0\) ，这样可以推出 \(\boldsymbol{S}_n\) 可逆。另外， \(\boldsymbol{S}_n\) 正定的一个充分条件是 \(\boldsymbol{R}_n\) 正定。如果 \(\boldsymbol{R}_n\) 非正定，情况会比较复杂，这里不做讨论。

简化的协方差更新方程¶

我们可以推导出一个简化的协方差更新方程：

推导过程如下，先将原始的协方差更新方程展开：

Summary¶

1. 初始化：输入初始时刻状态估计 \(\hat{\boldsymbol{x}}_{0\mid 0}\) 和初始时刻协方差估计 \(\boldsymbol{P}_{0\mid 0}\)
2. 预测阶段
   • 状态外插/转移/预测： \(\hat{\boldsymbol{x}}_{n+1\mid n} = \boldsymbol{F}\hat{\boldsymbol{x}}_{n\mid n} + \boldsymbol{G}\boldsymbol{u}_n\)
   • 协方差外插/预测： \(\boldsymbol{P}_{n+1\mid n} = \boldsymbol{F}\boldsymbol{P}_{n\mid n}\boldsymbol{F}^T + \boldsymbol{Q}_n\)
3. 更新阶段，上一时刻的预测（先验） \(\hat{\boldsymbol{x}}_{n+1|n}\) 即为这一时刻的 \(\hat{\boldsymbol{x}}_{n|n-1}\) .
   • 卡尔曼增益： \(\boldsymbol{K}_n = \boldsymbol{P}_{n\mid n-1}\boldsymbol{H}^T\left(\boldsymbol{H}\boldsymbol{P}_{n\mid n-1}\boldsymbol{H}^T + \boldsymbol{R}_n\right)^{-1}\)
   • 状态更新： \(\hat{\boldsymbol{x}}_{n\mid n} = \hat{\boldsymbol{x}}_{n\mid n-1} + \boldsymbol{K}_n (\boldsymbol{z}_n - \boldsymbol{H}\hat{\boldsymbol{x}}_{n\mid n-1})\)
   • 协方差更新（Joseph 形式）： \(\boldsymbol{P}_{n\mid n} = (\boldsymbol{I}-\boldsymbol{K}_n \boldsymbol{H})\boldsymbol{P}_{n\mid n-1}(\boldsymbol{I}-\boldsymbol{K}_n \boldsymbol{H})^T+ \boldsymbol{K}_n\boldsymbol{R}_n\boldsymbol{K}_n^T\)
4. 辅助方程
   • 测量方程： \(\boldsymbol{z}_n = \boldsymbol{H}\boldsymbol{x}_n+\boldsymbol{v}_n\)
   • 测量协方差： \(\boldsymbol{R}_n = \mathbb{E}\left(\boldsymbol{v}_n \boldsymbol{v}_n^T\right)\)
   • 过程噪声协方差： \(\boldsymbol{Q}_n = \mathbb{E}\left(\boldsymbol{w}_n \boldsymbol{w}_n^T\right)\)
   • 估计协方差： \(\boldsymbol{P}_{n\mid n} = \mathbb{E}\left(\boldsymbol{e}_n \boldsymbol{e}_n^T\right) = \mathbb{E}\left\{(\boldsymbol{x}_n-\hat{\boldsymbol{x}}_{n\mid n})(\boldsymbol{x}_n-\hat{\boldsymbol{x}}_{n\mid n})^T \right\}\)

数值计算实现时，求逆运算例如 \(\left(\boldsymbol{H}\boldsymbol{P}_{n\mid n-1}\boldsymbol{H}^T + \boldsymbol{R}_n\right)^{-1}\) 尽量不直接求逆，而是使用 Cholesky 分解更快更稳定，后面介绍的 EKF、IEKF、UKF 等也是如此。

在其他教科书或文献中，卡尔曼滤波中的预测值也写作 \(\hat{\boldsymbol{x}}_k^-,\;\boldsymbol{P}_k^-\) ，估计值也写作 \(\hat{\boldsymbol{x}}_{k},\;\boldsymbol{P}_k\) .

符号汇总： \(n_x\) 为状态向量中状态的个数， \(n_z\) 为测量到的状态数， \(n_u\) 为输入向量中元素个数。

Code¶

下面给出一个线性卡尔曼滤波的 Python 实现：

from dataclasses import dataclass

import numpy as np
from scipy.linalg import cho_factor, cho_solve


@dataclass
class LinearGaussianModel:
    """A linear Gaussian state-space model for Kalman filtering."""

    state_transition: np.ndarray  # F
    observation: np.ndarray  # H
    process_noise_cov: np.ndarray  # Q
    measure_noise_cov: np.ndarray  # R
    control_input: np.ndarray | None = None  # B


class KalmanFilter:
    """A Kalman filter for linear Gaussian state-space models."""

    def __init__(
        self,
        model: LinearGaussianModel,
        init_state_mean: np.ndarray,
        init_state_cov: np.ndarray,
    ) -> None:
        """Initialize the Kalman filter with the given model and initial state.

        Args:
            model (LinearGaussianModel): The linear Gaussian model.
            init_state_mean (np.ndarray): Initial state mean.
            init_state_cov (np.ndarray): Initial state covariance.
        """
        self.model = model
        self.state_mean = init_state_mean.copy()
        self.state_cov = init_state_cov.copy()

    def predict(
        self, control_vector: np.ndarray | None = None
    ) -> tuple[np.ndarray, np.ndarray]:
        """Perform the prediction step of the Kalman filter.

        Args:
            control_vector (np.ndarray | None, optional): Control vector. Defaults to None.

        Returns:
            tuple[np.ndarray, np.ndarray]: Predicted state mean and covariance.
        """
        F = self.model.state_transition
        Q = self.model.process_noise_cov
        B = self.model.control_input

        # Predict the next state mean.
        if B is not None and control_vector is not None:
            self.state_mean = F @ self.state_mean + B @ control_vector
        else:
            self.state_mean = F @ self.state_mean

        # Predict the next state covariance.
        self.state_cov = F @ self.state_cov @ F.T + Q

        return self.state_mean, self.state_cov

    def project(self) -> tuple[np.ndarray, np.ndarray]:
        """Project the current state into the observation space.

        Returns:
            tuple[np.ndarray, np.ndarray]: Projected mean and covariance.
        """
        H = self.model.observation
        R = self.model.measure_noise_cov

        # Projected mean and covariance in observation space.
        projected_mean = H @ self.state_mean
        projected_cov = H @ self.state_cov @ H.T + R

        return projected_mean, projected_cov

    def update(self, measurement: np.ndarray) -> tuple[np.ndarray, np.ndarray]:
        """Perform the update step of the Kalman filter with the given measurement.

        Args:
            measurement (np.ndarray): Measurement vector.

        Returns:
            tuple[np.ndarray, np.ndarray]: Updated state mean and covariance.
        """
        H = self.model.observation
        R = self.model.measure_noise_cov

        # Compute the Kalman gain.
        # Use Cholesky decomposition for matrix inversion.
        S = H @ self.state_cov @ H.T + R
        K = cho_solve(
            cho_factor(
                S,
                lower=True,
                overwrite_a=True,
                check_finite=False,
            ),
            H @ self.state_cov.T,
            overwrite_b=True,
            check_finite=False,
        ).T

        # Update the state mean and covariance.
        self.state_mean = self.state_mean + K @ (measurement - H @ self.state_mean)
        I_n = np.eye(self.state_cov.shape[0])
        self.state_cov = (I_n - K @ H) @ self.state_cov @ (I_n - K @ H).T + K @ R @ K.T

        return self.state_mean, self.state_cov

Appendix¶

卡尔曼滤波估计的目标是最小均方误差（Minimum Mean Square Error, MMSE）。在线性高斯模型（状态转移、观测都是线性的，先验分布和噪声均为高斯分布）的假设下，MMSE 可以等价于最大后验估计（Maximum A Posteriori, MAP），也就是说，卡尔曼滤波给出的估计既是最小均方误差解，也是最大后验解。下面来简单解释一下。

MMSE 估计：给定观测 \(z\) 后，选择一个估计 \(\hat{x}\) 最小化条件期望的二次误差：

对任意分布，最小化平方损失的最佳点就是条件均值，因此：

MAP 估计：给定观测 \(z\) 后，选择使后验概率密度最大的点（后验众数）：

若后验为高斯分布，概率密度最大值即为均值处，因此 \(\hat{x}_{\text{MAP}}=\mu\) .

因此，当后验分布为高斯分布，有 \(\hat{x}_{\text{MMSE}}=\hat{x}_{\text{MAP}}\) .

对于单次观测，考虑最简单的的情形：先验分布为高斯分布 \(x\sim\mathcal{N}(m,P)\) ，线性观测模型包含高斯噪声 \(z=Hx+v,\;v\sim\mathcal{N}(0,R)\) .

由 Bayes 定理，后验概率 \(p(x\mid z)\propto p(z\mid x)\;p(x)\) ，写出他的概率分布：

这是关于 \(x\) 的一个严格凸的二次型，配方可得后验分布仍是高斯分布 \(x\mid z\sim\mathcal{N}(\mu,\Sigma)\) ，其中：

因此，MMSE 等价于 MAP，解即为条件均值 \(\mu\) .

同时，上式也等价于带先验约束的最小二乘问题：

随着时间递推：

若初始 \(x_0 \sim \mathcal{N}(m_0, P_0)\) ，则在每一步预测：

更新：

用贝叶斯链式法则可以证明，在线性-高斯闭包下， \(p(x_k \mid z_{1:k})\) 始终是高斯分布 \(\mathcal{N}(m_{k|k}, P_{k|k})\) ，因此 MMSE 和 MAP 等价。

Comments