Object Tracking 目标跟踪¶
在 Research - Object Detection 中,我们限定 YOLO 只从图像中识别一个 person 类的目标进行定位,限制条件太多,显然无法应对实际的多目标场景,这也体现了单纯目标检测的局限性。目标检测通常只能检测出图片或者视频流中的目标具体属于哪一类别,并不能直接长时间的追踪这个目标,此时就需要使用目标跟踪算法来实现这一目的。
例如 YOLO 只能从图中检测出目标类别、边界框、置信度等帧间独立的信息,但是无法得知目标的特征信息,也就无法从连续的图像中得知是否为某一具体的目标。也就是说,从结果上来看,YOLO 能持续识别到多个目标,但是它本身不知道这是同一个目标、同一个物体。
Track Mode in Ultralytics YOLO
在早期的 YOLOv3–YOLOv5,YOLO 只负责目标检测(Detection),也就是输出边界框。从 YOLOv8 开始,官方 CLI 和 API 内置了多目标跟踪模块,也就是 Task 中的 Track Mode,参考 Multi-Object Tracking with Ultralytics YOLO。但是 YOLO 自身仍然只负责检测部分,而 “Track” 功能其实是集成了外部 MOT 算法,如 ByteTrack、BoT-SORT、StrongSORT 等,整体上是 Tracking-by-Detection 架构。YOLO 负责输出检测框,Tracker 负责将同一目标在不同帧关联起来。
可一次完成“检测 + 跟踪 + ID 分配 + 输出轨迹”的任务。
目前 YOLO Track 的局限性在于,使用的 Tracking-by-Detection 架构中检测与跟踪分离,非联合优化,无法端到端学习。
目标跟踪(Object Tracking)是自动驾驶中的常见任务,根据跟踪目标数量的不同,目标跟踪可分为:
- 单目标跟踪(Single Object Tracking,SOT)
- 多目标跟踪(Multi-Objects Tracking,MOT)
1. MOT Basic¶
由于单目标跟踪相对较为简单,且可以看作是多目标跟踪的特殊情况,因此这里主要讨论的都是多目标跟踪算法。
多目标跟踪算法可以为两类,分别是基于检测的跟踪(TBD,Tracking-by-Detection)和联合检测跟踪(JDT,Joint Detection & Tracking)。基于检测的跟踪结构简单,跟踪效果与检测效果联系紧密,而联合检测跟踪类算法通常融合了多模块联合学习,在多项跟踪评价指标中表现出色。1
典型的多目标跟踪系统框架如下所示:
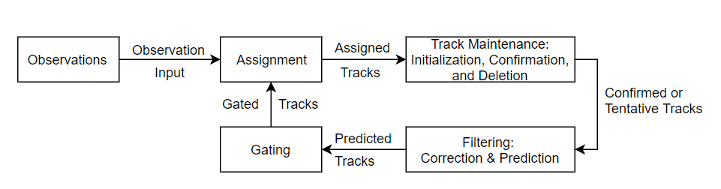
目标跟踪所要做的是根据传感器测量序列确定真实目标的数量以及每个目标的对应状态(位置、速度、航向等),具体实现可大体分为三部分:
- 状态估计
- 数据关联
- 航迹管理
其中,数据关联(Data Association)是目标跟踪中最具挑战的任务之一。对于单目标跟踪而言,数据关联要解决的是传感器测量能否与跟踪目标关联上;对于多目标跟踪而言,数据关联要解决的是哪个传感器测量能与哪个跟踪目标关联上,即跟踪目标与传感器测量的一一对应关系。目前,数据关联已发展出多种理论与算法,包括但不限于:
- 最近邻(Nearest Neighbor,NN)
- 概率数据关联(Probability Data Association,PDA)
- 联合概率数据关联(Joint Probability Data Association,JPDA)
- 多假设跟踪(Multiple Hypothesis Tracking,MHT)
- 随机有限集(Random Finite Set,RFS)
- 匈牙利算法(Hungarian Algorithm)
The following content is generated by ChatGPT.
多目标跟踪的两大路线:
| 技术路线 | 核心思想 | 特点 | 代表算法 |
|---|---|---|---|
| Tracking-by-Detection | 两阶段,先检测目标(如行人、车辆),再将相邻帧关联检测结果。 | 主流路线;比较依赖检测精度;关联策略关键。 | SORT、DeepSORT、ByteTrack、BoT-SORT、OC-SORT、StrongSORT 等 |
| Joint Detection and Tracking | 将目标检测和特征提取(ReID)在同一网络中联合学习,同时得到目标位置 + 外观特征 + ID。 | 端到端,实时性更好,但较为复杂、检测精度略差、难以扩展。 | JDE、FairMOT、CenterTrack、TransTrack、TrackFormer 等 |
按照类型可以归纳为:
| 类别 | 算法 | 使用 ReID | 速度 | 鲁棒性 | 优势场景 |
|---|---|---|---|---|---|
| 传统几何型 | SORT | ❌ | ⭐⭐⭐⭐ | ⭐ | 静态、无遮挡场景 |
| OC-SORT | ❌ | ⭐⭐⭐⭐ | ⭐⭐⭐ | 稍复杂场景 | |
| 外观增强型 | DeepSORT | ✅ | ⭐⭐⭐ | ⭐⭐⭐⭐ | 遮挡、行人 |
| BoT-SORT | ✅ | ⭐⭐ | ⭐⭐⭐⭐⭐ | 相机运动场景 | |
| StrongSORT | ✅ | ⭐⭐ | ⭐⭐⭐⭐⭐ | 大遮挡场景 | |
| 检测联合型 | JDE | ✅ | ⭐⭐⭐ | ⭐⭐⭐ | 实时端到端 |
| FairMOT | ✅ | ⭐⭐⭐ | ⭐⭐⭐⭐ | 行人跟踪标准 | |
| ByteTrack | ❌ | ⭐⭐⭐⭐ | ⭐⭐⭐⭐ | 各类目标、通用 | |
| Transformer 型 | CenterTrack | ❌ | ⭐⭐⭐ | ⭐⭐⭐ | 中等复杂场景 |
| TransTrack / MOTR | ✅ | ⭐ | ⭐⭐⭐⭐ | 高精度、研究级 |
常用的基础评价指标:
| 指标 | 全称 | 含义 | 备注 |
|---|---|---|---|
| TP | True Positive | 检测框与真值框匹配成功(IoU > 阈值) | 检测到一个人,而且框得很准。越大越好。 |
| FP | False Positive | 检测出了不存在的目标 | 没有人却输出了框,或同一人重复输出多个框。越小越好。 |
| FN | False Negative | 真值中有目标却没检测出来 | 有人但被漏检。越小越好。 |
| FP% | False Positive Rate | FP 在所有检测结果中的比例,即误检比例 | FP / (TP + FP) ,越小越好。 |
| FN% | False Negative Rate | FN 在所有真值(GT, ground truth)中的比例,即漏检比例 | FN / (TP + FN) ,越小越好。 |
| IDSW | ID Switch | 同一个人被赋予不同 ID,或不同人被错误合并 | 跟踪过程中 ID 更换,或两人 ID 互换。越小越好。 |
| MT | Most Tracked | 被正确跟踪时间比例大于 80% 的目标数 | 越大越好。 |
| ML | Most Lost | 被正确跟踪时间比例小于 20% 的目标数 | 越小越好。 |
| PT | Partially Tracked | 被正确跟踪时间比例在 20%~80% 之间的目标数 | |
| FM | Fragmentation | 跟踪中断次数 | 每个真值轨迹断开的次数求和。越小越好。 |
在此基础上,有以下常用高级指标:
1、MOTA(Multiple Object Tracking Accuracy),定义为:
数值越大越好。综合反映跟踪的正确性,考虑了误检、漏检和 ID switch,简单直观。缺点是对 ID 一致性权重较低。有些地方还能见到 mMOTA,代表平均 MOTA。
2、MOTP(Multiple Object Tracking Precision),定义为:
含义是对所有成功匹配的检测计算平均 IoU,数值越大越好。衡量检测框与真实框的平均 IoU,衡量空间定位精度,与检测性能强相关,与跟踪关联几乎无关。
3、IDF1(Identification F1 Score),定义为:
数值越大越好。其中:
- IDTP 为 ID 匹配正确的轨迹数。
- IDFP 为错误分配的 ID 数;
- IDFN 为未能匹配的真实 ID 数。
可以衡量跟踪算法在整个序列中维持 ID 一致性、轨迹连续性的能力。缺点是不考虑检测性能,漏检仍可能得高分。
4、HOTA(Higher Order Tracking Accuracy),定义为:
数值越大越好。其中,DetA(Detection Accuracy)代表检测性能,AssA(Association Accuracy)代表关联性能,将 MOTA 与 IDF1 的思想结合起来,在评估检测(能否发现目标)和关联(ID一致性)时给予平衡权重。
5、FPS(Frames Per Second),为模型帧率。
6、FAF(False Alarms per Frame),定义为 FAF = FP / 总帧数 ,每帧平均误检数量,数值越低越好。
有常用公开数据集:
| 数据集 | 场景 | 特点 | 标注类别 |
|---|---|---|---|
| MOT15 / 16 / 17 / 20 | 行人跟踪 | 最经典的 MOTChallenge 系列 | person |
| DanceTrack (2022) | 群舞场景 | 同外观高遮挡 | person |
| KITTI MOT | 车载 | 自动驾驶视角 | car, pedestrian |
| BDD100K MOT | 大规模城市道路 | 多类别、多天气 | car, person, rider… |
| TAO / TAO-MOT | 通用场景跟踪 | 类别多,尺度变化大 | 多类目标 |
| VisDrone / UAVDT | 航拍 | 目标小、运动剧烈 | person, car |
| CrowdHuman | 行人密集 | 行人检测与 ReID 联合 | person |
在介绍具体的工程算法之前,我们先介绍常用的数学理论算法——匈牙利算法。
2. Kuhn Algorithm (unweighted Hungarian)¶
以下部分内容参考匈牙利算法-看这篇绝对就够了!-CSDN博客。
匈牙利算法(Hungarian Algorithm)一种求解最优匹配问题的经典算法,用于在代价矩阵中找到任务与工人之间的最优一对一分配,使总代价最小(或收益最大)。其核心思想是通过矩阵行列变换和零元素匹配,逐步寻找完美匹配并调整未匹配元素的权值,从而得到最优解。
匈牙利算法一般使用的是带权无向图,我们可以先从特殊情况——无权无向图开始讨论,此时退化为 Kuhn Algorithm。接下来,我们需要回顾一些离散数学中的知识(以下内容摘自艾颖华老师《离散数学讲义》):
Definition¶
- 称 \(G\) 是二部分图(二部图),如果可以将 \(V(G)\) 表示为两个子集的不交并 \(G=A\cup B\) ,使得 \(A\) 中的顶点彼此不相邻、 \(B\) 中的顶点彼此不相邻,记为二部图 \(G=(A,B,E)\) .
- 二部图 \(G=(A,B,E)\) 的一个匹配,是指边集 \(E\) 的一个子集 \(M\) ,要求 \(M\) 的成员没有公共顶点。
- 称匹配 \(M\) 是从 \(A\) 到 \(B\) 的一个完全匹配,如果对 \(A\) 中每一个顶点 \(a\in A\) ,满足 \(M\) 中都有以 \(a\) 为顶点的边。进一步地,称 \(M\) 为完美匹配(perfect matching),如果每个顶点都是 \(M\) 中某个边的端点。
- 设 \(M\) 是二部图 \(G = (A \cup B, E)\) 的一个匹配,称 \(G\) 的顶点 \(v\) 是自由顶点,如果 \(M\) 中没有以 \(v\) 为顶点的边。
- 称简单路 \(P\) 是相对于匹配 \(M\) 的增广路(augmenting path),如果 \(P\) 的起点 \(u\) 是 \(A\) 的自由顶点,终点是 \(B\) 的自由顶点,且 \(P\) 的第偶数条边都属于 \(M\),其余边属于 \(E - M\)。换句话说,简单路 \(P\) 是增广路,如果它的端点都是自由顶点,且属于 \(M\) 的边与不属于 \(M\) 的边在 \(P\) 上交替出现。
上面的数学语言略显抽象,我们使用更加通俗易懂的语言重新描述一遍:
- 二部图 \(G=(A\cup B, E)\) :顶点划分为左右两部分 \(A,B\) ,只存在连接 \(A,B\) 之间的边,不存在 \(A,B\) 内部的边。
- 匹配 \(M\) :边集的一个子集,任意两条边无公共端点,相当于给工人一一分配任务。
- 完全匹配/最大匹配:边数最多的匹配,再加任何一条就会冲突,且不一定覆盖所有顶点。
- 完美匹配:图中每个点都被匹配到。这要求图的顶点数一定为偶数。
- 自由顶点:匹配 \(M\) 中没有边连接的顶点。
- 简单路:没有重复顶点的道路。
- 增广路:起点和终点都是自由顶点,沿着路径走,属于 \(M\) 的边和不属于 \(E-M\) 的边交替出现。由于首尾边都不属于 \(M\) ,因此整条路的边数一定为奇数。
另外,完美匹配就像是一个定义到 \(A\) 和 \(B\) 之间的双射,两个集合中的元素一一对应,就像是 \(n\) 个男人和 \(n\) 个女人,他们之间可能互有好感(一个男人可能对多个女人有好感,一个女人可能对多个男人有好感,及每个顶点都可能有多条连接其他顶点的边),完美匹配就是找到一种配偶方式,使得每一对配偶都是互有好感的。但实际中,我们通常很难做到完美匹配,但是可以做到完全匹配。完全匹配相当于,撮合任何一对互有好感的男女,最多能成全多少对情侣。那么如何找到完全匹配?关键就是找到增广路径。
Algorithm¶
Berge's lemma: \(M\) 是 \(G\) 的完全匹配的充要条件是,不存在相对于 \(M\) 的增广路径。
Hall's marriage theorem: 二部分图 \(G=(A\cup B,E)\) 存在 \(A\to B\) 完全匹配的充要条件是, \(\forall S\subseteq A\) 都有 \(|N(S)|\geqslant |S|\) 。其中 \(N(S)\) 是 \(S\) 集中所有点的邻点的集合。
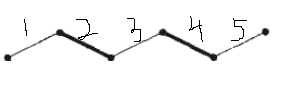
例如上面的图,边集“2,4”是一个匹配,但同时边集“1,3,5”也是一个匹配,而且边数更多。如果我们从边“2,4”出发,会发现“1,2,3,4,5”是一个增广路径,而去除“2,4”之后就得到了一个更大的匹配。因此自然地,寻找完全匹配就是在已有匹配的情况下,不断寻找增广路径,因为出现一条增广路径,就意味着匹配中可以增加一条边。
我们来看一个例子:
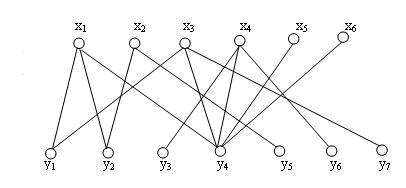
对于这样一个二部图,我们从左向右寻找完全匹配,我们的目标是尽可能给 \(X\) 中最多的点找到到配对。注意,完全匹配是互相的,如果我们给 \(X\) 找到了最多的 \(Y\) 中的对应点,同样, \(Y\) 中也不可能有更多的点得到匹配。
初始时,我们选择 \((x_1,y_1)\) 边构建匹配,已配对的边加粗。
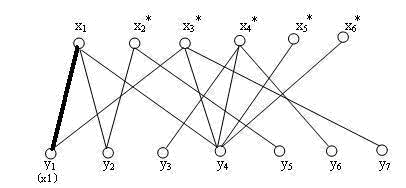
接下来给 \(x_2\) 添加匹配 \((x_2,y_2)\) :
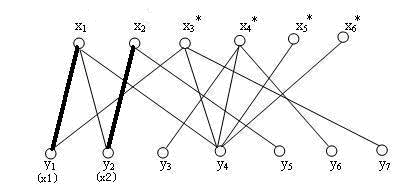
接下来,给 \(x_3\) 添加匹配的时候,发现它的第一条边的另一端 \(y_1\) 已经被 \(x_1\) 占用,于是抢走了 \(y_1\) ,而 \(x_1\) 重新寻找匹配,发现第二条边的另一端 \(y_2\) 已经被 \(x_2\) 占用,于是抢走了 \(y_2\) ,而 \(x_2\) 重新寻找匹配,直接匹配到 \(y_5\) 。这样的“发现冲突-抢占-重新寻找匹配”的操作也是一个递归的过程。
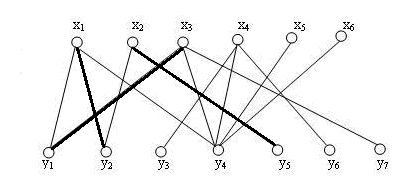
在上述过程中涉及到的顶点,依次为 \(P=(x_3,y_1,x_1,y_2,x_2,y_5)\) ,我们发现组成的这条路径竟然是匹配 \(M=(x_1-y_1,x_2-y_2)\) 的一个增广路径!Amazing!我们将 \(M\) 中的配对点拆分开,重新组合,得到了一个更大匹配 \(M'=(x_1-y_2,x_2-y_5,x_3-y_3)\) 。
此时还有一个问题,那就是上述操作中,各个顶点依次挤掉其他的顶点,最后一个顶点发现还是有归宿的。但是如果最后发现最后一个点没有其他可用的匹配了呢?例如 \(x_2\) 没有连接 \(y_5\) ,那就意味着增广路径寻找失败,新到来的点 \(x_3\) 无法加入到当前匹配,将会寻找下一个顶点 \(x_4\) 的匹配。
最后把 \(x_4,x_5\) 配对,得到这个图的一个完全匹配:
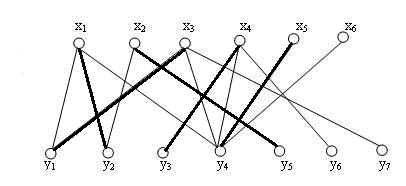
最后总结一下,匈牙利算法的核心,就是不断寻找原有匹配 \(M\) 的增广路径,由此,这条增广路径减去 \(M\) 就得到一个更大的匹配 \(M'\) ,恰好比 \(M\) 多一条边。对于一般的图来说,完全匹配可能不唯一,但是完全匹配的大小是唯一的。
Code¶
接下来给出一个匈牙利算法的简单 Python 实现,二部图使用邻接链表(adjacency list)表示,以及一个 C++ 实现,二部图使用邻接矩阵表示(adjacency matrix):
# Generated by ChatGPT
def hungarian(adj: list[list[int]]) -> dict[int, int]:
"""匈牙利算法 (DFS 版本),求解二部图最大匹配
本函数使用深度优先搜索 (DFS) 实现无权二部图的最大匹配算法。
输入为左侧顶点的邻接表,输出右侧顶点的匹配结果。
Args:
adj (List[List[int]]):
二部图的邻接表。
其中 adj[u] 表示左侧顶点 u 能连接的所有右侧顶点编号列表。
顶点编号通常从 0 开始计数。
Returns:
dict[int, int]:
一个字典,表示匹配结果。
键为右侧顶点编号 (v),值为与之匹配的左侧顶点编号 (u)。
例如 {1: 0, 2: 3} 表示右顶点1匹配左顶点0,右顶点2匹配左顶点3。
Example:
>>> adj = [
... [1, 2], # 左侧顶点0
... [1, 3], # 左侧顶点1
... [2, 3], # 左侧顶点2
... [2, 4] # 左侧顶点3
... ]
>>> hungarian(adj)
{1: 0, 2: 2, 3: 1, 4: 3}
"""
matched = {}
def match(u: int, visited: set) -> bool:
for v in adj[u]:
if v in visited:
continue
visited.add(v)
if v not in matched or match(matched[v], visited):
# 如果 v 还没有匹配,或者能为 v 当前的匹配重新找一个位置
matched[v] = u
return True
return False
for u in range(len(adj)):
# 必须在外部初始化空集合,因为递归过程需要共享 visited
visited = set()
match(u, visited)
return matched
if __name__ == "__main__":
adj = [
[1, 2], # 左侧顶点0
[1, 3], # 左侧顶点1
[2, 3], # 左侧顶点2
[2, 4], # 左侧顶点3
]
result = hungarian(adj)
print(result)
// Generated by ChatGPT
#include <iostream>
#include <vector>
// 尝试为左侧顶点 u 寻找匹配
bool match(int u,
const std::vector<std::vector<int>> &adj,
std::vector<int> &matched,
std::vector<bool> &visited)
{
int n_right = adj[0].size();
for (int v = 0; v < n_right; v++)
{
if (adj[u][v] && !visited[v])
{
visited[v] = true;
if (matched[v] == -1 || match(matched[v], adj, matched, visited))
{
matched[v] = u;
return true;
}
}
}
return false;
}
// 匈牙利算法函数
std::vector<int> hungarian(const std::vector<std::vector<int>> &adj)
{
int n_left = adj.size();
int n_right = adj[0].size();
std::vector<int> matched(n_right, -1); // matched[v] = 与右顶点 v 匹配的左顶点编号
for (int u = 0; u < n_left; u++)
{
std::vector<bool> visited(n_right, false);
match(u, adj, matched, visited);
}
return matched;
}
int main()
{
// 邻接矩阵(1 表示连边,0 表示无边)
std::vector<std::vector<int>> adj = {
{1, 1, 0, 0}, // 左0连接右1,2
{1, 0, 1, 0}, // 左1连接右1,3
{0, 1, 1, 0}, // 左2连接右2,3
{0, 1, 0, 1} // 左3连接右2,4
};
// 调用算法
std::vector<int> res = hungarian(adj);
// 输出结果
std::cout << "匹配结果 (右 -> 左):\n";
for (int v = 0; v < (int)res.size(); ++v)
{
if (res[v] != -1)
std::cout << "右 " << v + 1 << " ← 左 " << res[v] << '\n';
}
return 0;
}
3. Kuhn-Munkres Algorithm (weighted Hungarian)¶
以下部分内容参考自:
上述讨论的简单情形的 Kuhn Algorithm 只能判断能否匹配,求解最大匹配,不关心代价,也无法求“最小代价匹配”。而真正需要最小化匹配代价的,是带有权重的匈牙利算法 Kuhn-Munkres Algorithm。它使用的是有权无向图,等价于一个代价矩阵。例如工人任务分配问题中,工人集合和任务集合组成一个二部分图,某个工人完成某项任务的代价即为连接该工人和该任务的边的权值。
KM 算法的目标是在带权二部图中寻找最佳一一匹配,也就是:
其中:
- \(c_{i,j}\) :左顶点 \(i\) 到右顶点 \(j\) 的代价;
- \(\pi(i)\) :表示 \(i\) 被分配到的右顶点;
- \(n\) :左、右两侧顶点数量相等(若不等可补零)。
这就是最小代价匹配(minimum-cost perfect matching),也叫任务分配问题(Assignment Problem)。
但如果要最大化权重问题,只需做简单变换:
只要把代价矩阵 cost = -weight,再调用最小化版本的 KM 即可。
因为很多 KM 实现(包括 scipy)不支持负权,因此通常加一个偏移量保证代价为正:
这样一来,越大的权重对应越小的代价,KM 算法仍然能正确求出最大权匹配,且不会产生负数问题。
Definition¶
- 顶标:是一个节点函数 \(l:V\to\mathbb{R}\) ,就是给每个顶点一个标号,可以简单理解为节点的值。
- 可行顶标:对所有顶标都满足 \(l(x)+l(y)\geqslant w(x,y),\forall x\in X,y\in Y\) ,也就是边的权值不能超过两个端点的顶标之和。KM 算法的顶标必须满足这一条件。
- 相等子图:图 \(G=(V,E)\) 的相等子图 \(G_l=(V,E_l)\) ,包含 \(G\) 的所有顶点,但是只包含边权值等于两个端点顶标之和的边,即 \(E_l=\{(x,y):l(x)+l(y)=w(x,y)\}\) .
Kuhn-Munkres 定理
如果 \(l\) 是可行顶标, \(M\) 是相等子图 \(E_l\) 的完美匹配,那么 \(M\) 是 \(G\) 的最大权匹配
证明:任取 \(G\) 的一个完美匹配 \(M'\) 都有不等式
说明任何一个完美匹配的边权值之和的上界就是所有顶标和,也等于完美匹配 \(M\) 的边权和,因此 \(M\) 是 \(G\) 的最大权值匹配。KM 定理将求最大权匹配问题转化成了求完美匹配问题。KM 算法的核心就在于寻找可行顶标,使得相等子图有完美匹配。可行顶标的修改过程中,每一步都运用了贪心的思想,这样我们的最终结果一定是最优的。
Algorithm¶
算法的大概框架为:
- 给定初始的可行顶标 \(l\) 和匹配 \(M\) .
- 当 \(M\) 不是相等子图 \(E_l\) 的完美匹配时,重复以下操作:
- 在 \(E_l\) 中搜索增广路径,如果存在,取反使得匹配数增加1。
- 如果搜索增广路径失败,将可行顶标 \(l\) 改进为 \(l'\) 使得 \(E_l\subset E_{l'}\) ,然后再重新搜索。
如果 \(G\) 存在完美匹配,那么每次迭代过程中,要么匹配数增加1,要么相等子图扩大,最终算法一定会停止,停止时的 \(M\) 就是 \(E_l\) 的完美匹配,也是 \(G\) 的最大权匹配。
初始时刻,我们构造一个简单的可行顶标: \(Y\) 的顶标全部取0, \(X\) 的顶标取每个点所连的边的最大权值
这样显然满足可行顶标的要求。如果把这些最大权重对应的边找出来,其实就得到了相等子图。
初始匹配可设置为空集 \(M=\varnothing\) .
改进可行顶标时,如果当前 \(M\) 不是相等子图 \(E_l\) 的完美匹配,是因为当前某个未匹配顶点(自由顶点) \(u\) 出发,我们找不到它出发的一条增广路径,只能找到一个交替路径(以匹配的边和未匹配的边交替,但两端不都是自由顶点。至于为什么一定能找到交替路,稍后会解释)。我们定义 \(X\) 中在交替路 \(P\) 中的点集称为 \(S=\{x\mid x\in P\cap X\}\) 、不在交替路中的点集为 \(S'=X\backslash S\) , \(Y\) 中在交替路 \(P\) 中的点集称为 \(T=\{y\mid y\in P\cap Y\}\) 、不在交替路中的点集为 \(T'=Y\backslash T\) .
如果我们把交替路中 \(X\) 集顶点的顶标全都减小某个值 \(\alpha_l\) ,同时 \(Y\) 集的顶标全都增加同一个值 \(\alpha_l\) ,那么我们会发现:
- 两端都在交替路中的边 \(e_{i \to j}\) , \(l(i)+l(j)\) 的值不变。也就是说,它原来属于相等子图,现在仍属于相等子图。
- 两端都不在交替路中的边 \(e_{i \to j}\) , \(l(i)+l(j)\) 的值不变。也就是说,它原来属于(或不属于)相等子图,现在仍属于(或不属于)相等子图。
- \(X\) 端在 \(S'\) 中, \(Y\) 端在 \(T\) 中的边 \(e_{i \to j}\) ,它的 \(l(i)+l(j)\) 的值增大。也就是说,它原来不属于相等子图,现在仍不可能属于相等子图。
- \(X\) 端在 \(S\) 中, \(Y\) 端在 \(T'\) 中的边 \(e_{i \to j}\) ,它的 \(l(i)+l(j)\) 的值减小。也就是说,它原来不属于相等子图,现在可能进入了相等子图,因而使相等子图得扩大。
也就是说,只有 \(X\) 集一端在 \(S\) 中, \(Y\) 端在 \(T'\) 中的边才有可能被选中。继续贪心,我们只选择满足条件的边权最大的边被选中,即满足 \(l(x)+ l(y) = w(x,y)\) ,那么就应该取 \(\alpha_l= \min\{l(x) + l(y) - w(x,y) \mid x \in S, y \in T'\}\) .
然后给所有顶点赋新的顶标:
\(l'\) 也是一个可行顶标。于是有新的边加入相等子图,我们可以继续对未匹配顶点 \(u\) 寻找增广路。这样的修改最多进行 \(O(n)\) 次,而一共有 \(n\) 个点,所以除去修改顶标的时间,复杂度已经达到 \(O(n^2)\) 。因此,算法的复杂度主要取决于修改顶标的时间。
思路一:枚举所有 \(n^2\) 条边,看是否满足条件,满足条件就更新 \(\alpha_l\) 值。该方法最直观清晰,然而总的复杂度高达至 \(O(|V|^4)\) 。
思路二:对于 \(T'\) 的每个点 \(v\) ,定义松弛变量 \(slack(v)=\min\{l(x) + l(y) - w(x,y)\mid x \in S \}\),这个松弛变量在匹配的过程中就可以更新,修改顶标的过程中 \(\alpha_l=\min\{ slack(v) \mid v \in T' \}\) ,总复杂度 \(O(|V|^3)\) 。这样做但不是严格的,但实际上已经够用。
最终的伪代码如下:
-
初始化可行顶标 \(l\) 和相等子图 \(E_l\) 的初始匹配 \(M\) :
\[ \forall y\in Y,\;l(y)=0,\quad \forall x\in X,\;l(x)=\max_{y\in Y}\{w(x,y)\},\quad M=\varnothing \] -
若 \(M\) 是 \(E_l\) 的完美匹配,终止算法。否则选取自由顶点 \(u\in X\) ,令 \(S=\{u\},\;T=\varnothing\) .
-
若 \(N_l(S)=T\) ,更新可行顶标:
\[ \alpha_l= \min_{x \in S, y \in Y\backslash T} \{l(x) + l(y) - w(x,y)\},\quad l'(v)=\begin{cases} l(v)-\alpha_l, &v\in S \\ l(v)+\alpha_l,& v\in T \\ l(v),&\text{else} \end{cases} \] -
若 \(N_l(S)\neq T\) ,取 \(v\in Y\backslash T\) :
- 若 \(v\) 是自由顶点,那么找到了一条 \(u\to v\) 的增广路径,取反使匹配数增加1,跳转至 Step 2。
- 若 \(v\) 不是自由顶点,设当前 \(v\) 已经和 \(z\) 匹配,则令 \(S=S\cup\{z\},\;T=T\cup\{v\}\) ,跳转至 Step 3。
Code¶
# Generated by ChatGPT
import random
def km_max(a):
"""Return (match, max_sum). match[i]=j for original left i, maximizing sum a[i][j]."""
n, m = len(a), len(a[0]) if a else 0
N = max(n, m)
# pad to square
w = [[0] * N for _ in range(N)]
for i in range(n):
wi = w[i]
ai = a[i]
for j in range(m):
wi[j] = ai[j]
u = [max(row) for row in w] # left labels
v = [0] * N # right labels
matchR = [-1] * N # which left is matched to right j
for i_start in range(N):
# Hungarian "Dijkstra-like" search with slacks
visitedL = [False] * N
visitedR = [False] * N
slack = [float("inf")] * N # minimal reduced cost to reach right j
slackx = [-1] * N # which left i gives that slack
prevR = [-1] * N # predecessor left for right j along the tree
i0 = i_start
prev_j = -1
for j in range(N):
slack[j] = u[i0] - v[j] - w[i0][j]
slackx[j] = i0
while True:
# select right vertex j with minimal slack among unvisited
jmin, d = -1, float("inf")
for j in range(N):
if not visitedR[j] and slack[j] < d:
d, jmin = slack[j], j
# adjust labels by d
for i in range(N):
if visitedL[i]:
u[i] -= d
for j in range(N):
if visitedR[j]:
v[j] += d
else:
slack[j] -= d
# add jmin to tree
visitedR[jmin] = True
i1 = matchR[jmin]
prevR[jmin] = slackx[jmin]
if i1 == -1: # found augmenting path, augment
# backtrack to augment
j = jmin
while j != -1:
i = prevR[j]
pj = -1
# find previous matched right for i
for jj in range(N):
if matchR[jj] == i:
pj = jj
break
matchR[j] = i
j = pj
break
else:
# grow alternating tree
visitedL[i1] = True
# update slacks using new left i1
for j in range(N):
if not visitedR[j]:
delta = u[i1] - v[j] - w[i1][j]
if delta < slack[j]:
slack[j] = delta
slackx[j] = i1
# extract matching and value for original (n x m)
match = [-1] * n
total = 0
for j in range(m):
i = matchR[j]
if 0 <= i < n:
match[i] = j
for i in range(n):
j = match[i]
if j != -1:
total += a[i][j]
return match, total
if __name__ == "__main__":
random.seed(42)
# 随机生成一个(可能非方阵)权矩阵,做“最大权匹配”
n, m = 5, 7
A = [[random.randint(1, 99) for _ in range(m)] for _ in range(n)]
match, max_sum = km_max(A)
print("Matrix ({}x{}):".format(n, m))
for row in A:
print(row)
print("\nMatching (left i -> right j):")
for i, j in enumerate(match):
print(f" {i} -> {j}")
print("\nMax total weight:", max_sum)
4. Munkres Algorithm (Assignment Problem)¶
之前的 Kuhn-Munkres Algorithm 中,是以图论的方法,解决最大权重/最小代价问题。而一般考虑 Assignment Problem 时,常使用矩阵下的匈牙利算法,也就是 Munkres Algorithm(matrix reduction)。
以下部分内容跟参考自:
Description¶
在任务指派问题(如 n 项工作由 n 个人承担,每个人完成不同工作所花时间不同,那如何分配使得花费的时间最少)以及一些多目标检测任务中的数据关联部分(如一个目标有多个特征点,有多个目标时检测到的特征点属于哪一个目标的问题)常常会看到 Munkres 算法,二分图匹配同样可以转换为指派问题,即将一侧的图看成工人,将另一侧的图看成任务,图与图之间的相似度可以转换成矩阵系数。
Munkres 算法的条件为:
- 系数矩阵(代价矩阵) \(C\in \mathbb{R}^{n\times n}\) 为 \(n\) 阶方阵,这样才可能存在完美匹配。
- 每一个系数为非负数 \(c_{ij}>0\) .
- 求解目标为总代价的最小值。
定义变量:
问题转化为:
也就是每一个人只能完成一项任务,每一项任务只能有一个任务完成,保证一一对应、完美匹配,体现在 \(X=(x_{ij})\) 上就是每一行、每一列有且仅有 1 个 1,其余全为 0。
Algorithm¶
首先我们介绍图论中的柯尼希定理(注意,与运动学中多质点系统的柯尼希定理不同):
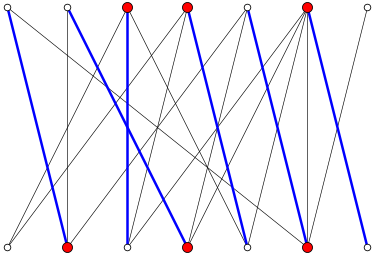
König's theorem:在二部分图中,最大匹配数等于最小顶点覆盖数。
所谓一个顶点覆盖,是指顶点集的一个子集,图中每一条边都至少有一个顶点在这个子集中。
例如,在图中的二部图中,最大匹配(蓝边)和最小顶点覆盖(红点)数均为6。
如果用矩阵的语言描述,就是:在一个 0-1 矩阵中,“互不在同一行同一列的0元素的最多个数”等于“能够覆盖所有 0 元素的最小直线(行或列)数”。
匈牙利算法会对矩阵进行行列减法,使得部分元素变成 0。实际上,这些变成 0 的位置,就可以看作相等子图的一条边。而矩阵中一行或者一列所覆盖的零元素,就代表某个顶点所有的连接数。
Mubkres 算法的具体步骤。
- 代价矩阵初始化:
- Row reduction:代价矩阵的每一行减去该行的最小值。
- Column reduction:代价矩阵的每一列减去该列的最小值。
-
这里用到的性质是,代价矩阵每一行或每一列减去一个相同的元素,最优解不变,因为最优解只关心如何分配指标和索引,不关心总代价的绝对大小。
- 尝试分配寻找可行解:用最少的直线(横、竖)覆盖矩阵中所有0元素,如果直线个数等于矩阵的阶数 \(n\) ,结束,否则执行 Step 3。
- 找到未被覆盖元素中的最小值 \(k\) ,所有未被覆盖的元素减去 \(k\) ,被覆盖两次的元素加上 \(k\) ,然后跳转至 Step 2。
下面看一个示例。我们有一个航迹测量代价矩阵,矩阵中元素表示航迹测量的匹配距离。
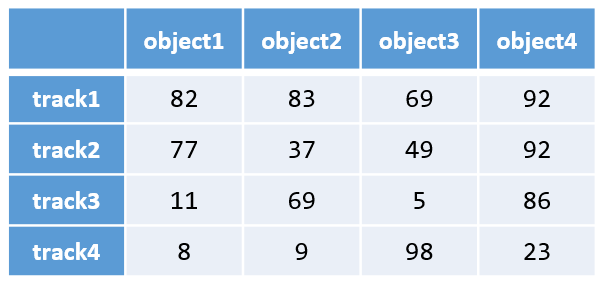
按照上述步骤,求解最小代价匹配的过程为:
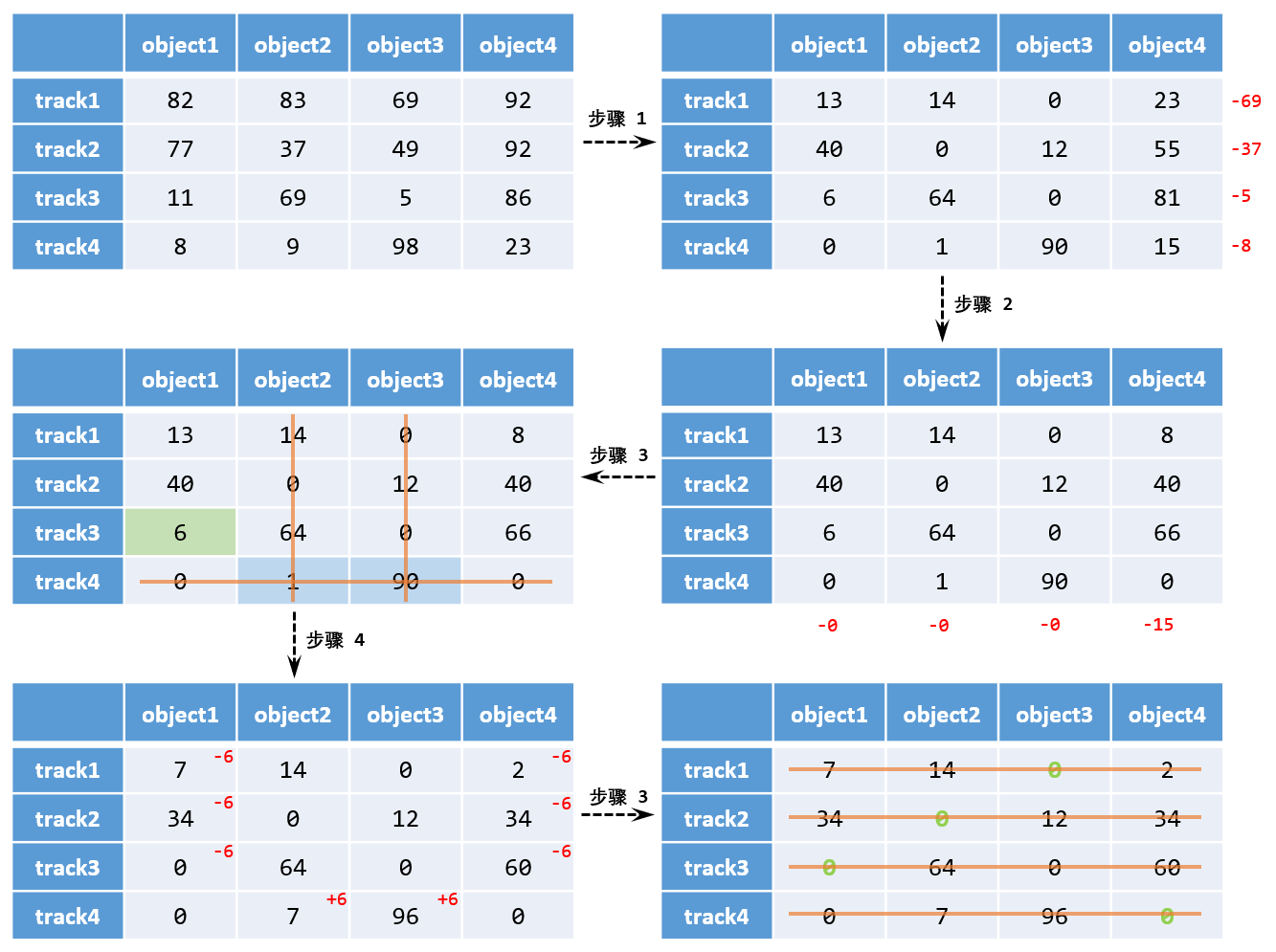
上述过程比较直观易懂,但是问题在于,虽然人眼可以看出哪些直线可以覆盖所有的 0,但是体现在代码上,如何找出覆盖所有 0 的最小的直线?
1957 年 James Munkres 引入了“标星 0(starred zeros)”和“标撇 0(primed zeros)”的概念以改进匈牙利算法原始流程中的划线法,在算法执行过程中会选择性地对代价矩阵中产生的 0 元素标记星号(*)或标记撇号(’)来辅助搜索增广路,标星 0 表示增广路中的匹配边,标撇 0 表示增广路中的未匹配边。
改进后的 Munkres 算法流程为:
- Cost Matrix Initialization
- Row reduction:代价矩阵的每一行减去该行的最小值。
- Column reduction:代价矩阵的每一列减去该列的最小值。
- Star Zeros(目标:在每一行放置互不冲突的 star,作为匹配的雏形)
- 逐行扫描矩阵,在每一行中,找到“不在 star 占用的列中的 0”,找到的第一个对它标记 star,并标记这个 star 所在行和列都被覆盖,继续下一行。
- 扫描完成后,如果所有 star 占用的列数等于矩阵的阶数 \(n\) ,说明每一列都有一个 star,已经完成一一配对,终止算法。
- 如果 star 没有覆盖全部的列,进入 Step 3。
- Priming & Augmentation 循环进行以下操作
- 在未被之前行和列覆盖的元素中,找到一个0并标记 prime,并查看这一行后是否有 star。如果没找到 0,直接进入 Step 4。
- 如果这一行没有 star,意味着找到了一条增广路径。构建增广路径:该 prime 为路径的首条边,若 prime 所在的列存在 star 则把 star 加入路径,若 star 所在的行存在 prime 则把 prime 加入路径,直到找不到 star 为止。把路径中所有 prime 变为 star,取消路径中所有 star 标记,然后清除所有 prime,取消所有行覆盖。最后,检查所有 star 覆盖的列数是否等于矩阵阶数 \(n\) ,如果等于,则找到完美匹配,终止算法,否则重新 Priming。
-
实际上,star 代表着暂时处于匹配中,prime 代表可能称为新的匹配,如果此时新加的 prime 的这一行没有 star,代表 prime 恰好比 star 多一个,也就构成了一条增广路径。这条增广路径从一个 prime 开始,找到同一列的 star,再从这个 star 找同一行的 prime,如此交替,知道遇到一个 prime 它所在的列没有 star。
- 如果这一行已有 star,就盖住这一行(行覆盖),把那个已有 star 所在的列取消列覆盖,重新回到这一步的开始“寻找未覆盖元素中的 0 标记 prime”。
- 生成新 0:找出未覆盖元素的最小值 \(d\) ,当前所有未覆盖元素都减去 \(d\) ,所有交叉覆盖(同时被行覆盖和列覆盖)的元素都加上 \(d\) ,其余元素不变。这样就能在未覆盖区域生成新的 0,然后开始 Step 3 的 Priming。
接着上面的例子,使用改进算法的流程为(第一步进行了膨胀补 0,保证代价矩阵为方阵) :
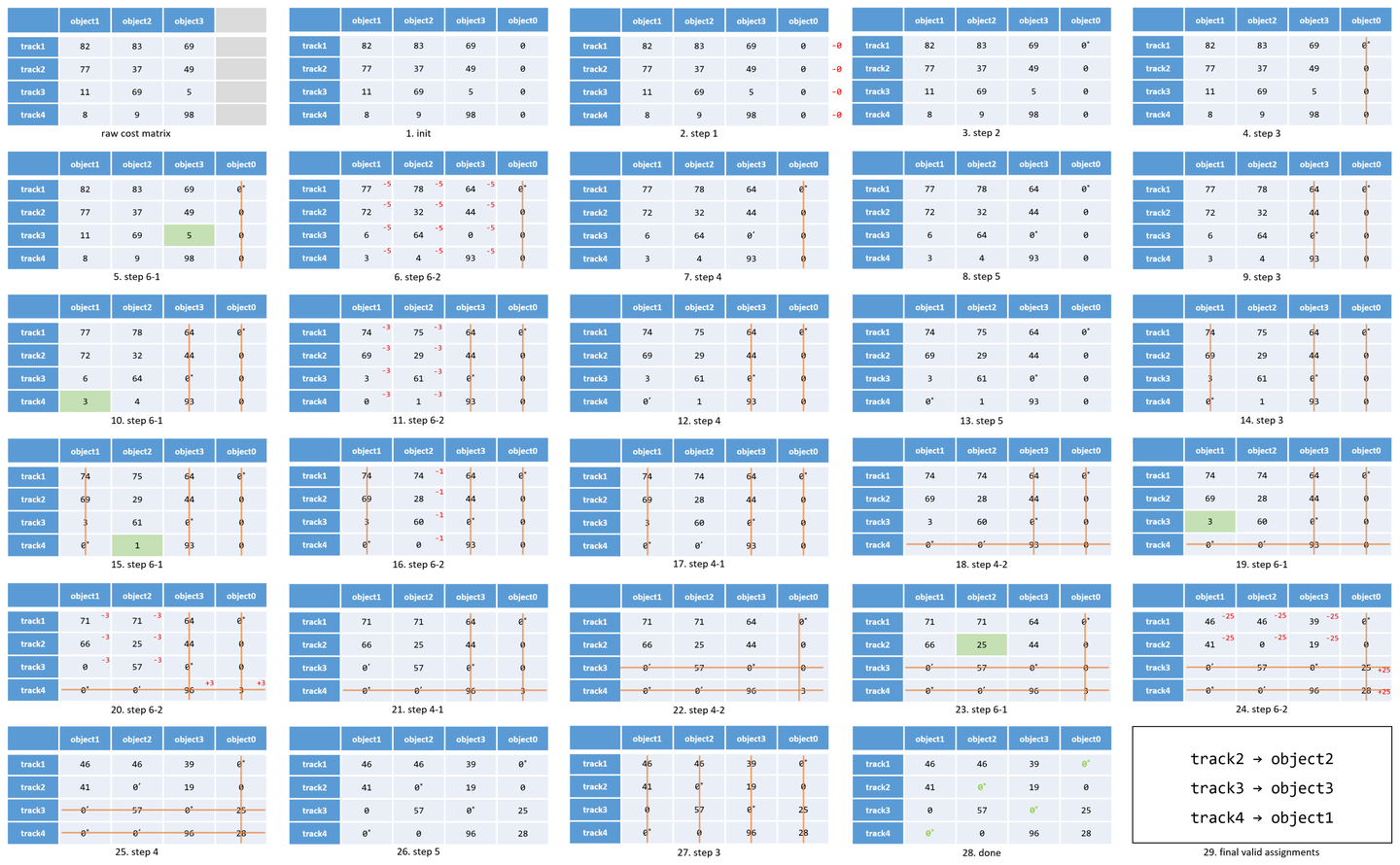
Follow-up problems¶
(1)如果不是求最小代价,是求最大代价,如何处理?
找出代价矩阵中的最大值 max,然后令代价矩阵变为“max-代价矩阵各元素值”,得到新代价矩阵,再按照正常匈牙利法求解。
(2)如果系数矩阵不是方阵?
- 人数 > 工作:增加虚拟工作,虚拟工作对应的代价全设为0。
- 人数 < 工作:增加虚拟工人,虚拟工人对应的代价全设为0。
(3)如果某个人可以做多项工作?
如果一个工人可以做 \(k\) 件事,那就把这个工人的代价复制 \(k\) 份,相当于增加了虚拟人数。如果不是方阵,再添加虚拟工作。
(4)如果某个人不能做某项工作?
将问题转换为求最小值后,如果第 \(i\) 个人不能做第 \(j\) 项工作,可将代价 \(c_{ij}\) 设置为一个比代价矩阵最大值更大的数。
Code¶
下面分别给出 Munkres 算法的 Python 和 C++ 实现。其中 Python SciPy 库提供的 scipy.optimize.linear_sum_assignment() 函数可以直接调用,最为简单;C++ 的实现还可以参考 Munkres' Assignment Algorithm - The Algorithm Workshop - Bevilacqua。
# Generated by ChatGPT
import numpy as np
def hungarian(cost):
cost = cost.copy().astype(float)
n = cost.shape[0]
# Step 1: 行列减法
cost -= cost.min(axis=1, keepdims=True)
cost -= cost.min(axis=0, keepdims=True)
# 初始化标记矩阵:0=无标记, 1=star, 2=prime
mark = np.zeros_like(cost, dtype=int)
row_cover = np.zeros(n, dtype=bool)
col_cover = np.zeros(n, dtype=bool)
# Step 2: 初始打星
for i in range(n):
for j in range(n):
if cost[i, j] == 0 and not row_cover[i] and not col_cover[j]:
mark[i, j] = 1 # star
row_cover[i] = col_cover[j] = True
break
row_cover[:] = False
col_cover[:] = np.any(mark == 1, axis=0)
def find_zero():
"""未覆盖区域内搜索0,返回矩阵索引"""
for i in range(n):
if not row_cover[i]:
for j in range(n):
if cost[i, j] == 0 and not col_cover[j]:
return i, j
return None, None
def find_star_in_row(r):
"""某一行中搜素第一个 star zero"""
c = np.where(mark[r] == 1)[0]
return c[0] if c.size else None
def find_star_in_col(c):
"""某一列中搜索第一个 star zero"""
r = np.where(mark[:, c] == 1)[0]
return r[0] if r.size else None
def find_prime_in_row(r):
"""某一行中搜索第一个 prime zero"""
c = np.where(mark[r] == 2)[0]
return c[0] if c.size else None
# Step 3 + Step 4 主循环
while col_cover.sum() < n:
# 寻找未覆盖的0
while True:
r, c = find_zero()
if r is None:
# Step 4: 生成新0
d = np.min(cost[~row_cover][:, ~col_cover])
cost[~row_cover, :] -= d
cost[:, col_cover] += d
else:
mark[r, c] = 2 # prime
star_c = find_star_in_row(r)
if star_c is None:
# 构建增广路径
path = [(r, c)]
while True:
star_r = find_star_in_col(path[-1][1])
if star_r is None:
break
path.append((star_r, path[-1][1]))
prime_c = find_prime_in_row(path[-1][0])
path.append((path[-1][0], prime_c))
# 翻转路径
for i, j in path:
mark[i, j] = 1 if mark[i, j] != 1 else 0
mark[mark == 2] = 0
row_cover[:] = False
col_cover[:] = np.any(mark == 1, axis=0)
break
else:
row_cover[r] = True
col_cover[star_c] = False
# 输出结果
result = np.zeros(n, dtype=int)
for i in range(n):
j = np.where(mark[i] == 1)[0][0]
result[i] = j
return result
# 示例
if __name__ == "__main__":
np.random.seed(0)
cost = np.random.randint(1, 21, size=(10, 10))
print("代价矩阵:\n", cost)
assign = hungarian(cost)
print("最优匹配结果:")
for i, j in enumerate(assign):
print(f"行 {i + 1} → 列 {j + 1}, 代价 = {cost[i, j]}")
print("总代价 =", cost[range(len(assign)), assign].sum())
# Generated by ChatGPT
import numpy as np
from scipy.optimize import linear_sum_assignment
np.random.seed(0)
cost = np.random.randint(1, 21, size=(10, 10))
print("代价矩阵:\n", cost)
# 默认求最小代价,若求最大代价使用 -cost
row_ind, col_ind = linear_sum_assignment(cost)
print("\n最优匹配结果:")
for r, c in zip(row_ind, col_ind):
print(f"行 {r + 1} → 列 {c + 1}, 代价 = {cost[r, c]}")
print("总代价 =", cost[row_ind, col_ind].sum())
// Generated by ChatGPT
#include <iostream>
#include <vector>
#include <utility>
#include <cstdlib>
#include <iomanip>
#include <cmath>
using namespace std;
vector<int> hungarian(const vector<vector<double>> &cost_matrix)
{
int n = cost_matrix.size();
vector<vector<double>> cost = cost_matrix;
vector<vector<int>> mark(n, vector<int>(n, 0)); // 0=none, 1=star, 2=prime
vector<bool> row_cover(n, false), col_cover(n, false);
// ---- Step 1: Row & Column reduction ----
for (int i = 0; i < n; i++) {
double minval = *min_element(cost[i].begin(), cost[i].end());
for (int j = 0; j < n; j++) cost[i][j] -= minval;
}
for (int j = 0; j < n; j++) {
double minval = 1e18;
for (int i = 0; i < n; i++) minval = min(minval, cost[i][j]);
for (int i = 0; i < n; i++) cost[i][j] -= minval;
}
// ---- Step 2: Star zeros ----
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
if (fabs(cost[i][j]) < 1e-9 && !row_cover[i] && !col_cover[j]) {
mark[i][j] = 1; // star
row_cover[i] = col_cover[j] = true;
break;
}
fill(row_cover.begin(), row_cover.end(), false);
for (int j = 0; j < n; j++)
for (int i = 0; i < n; i++)
if (mark[i][j] == 1)
col_cover[j] = true;
auto find_zero = [&]() -> pair<int,int> {
for (int i = 0; i < n; i++)
if (!row_cover[i])
for (int j = 0; j < n; j++)
if (!col_cover[j] && fabs(cost[i][j]) < 1e-9)
return make_pair(i, j);
return make_pair(-1, -1);
};
auto find_star_in_row = [&](int r) -> int {
for (int j = 0; j < n; j++) if (mark[r][j] == 1) return j;
return -1;
};
auto find_star_in_col = [&](int c) -> int {
for (int i = 0; i < n; i++) if (mark[i][c] == 1) return i;
return -1;
};
auto find_prime_in_row = [&](int r) -> int {
for (int j = 0; j < n; j++) if (mark[r][j] == 2) return j;
return -1;
};
// ---- Step 3 + 4 loop ----
while (count(col_cover.begin(), col_cover.end(), true) < n)
{
while (true)
{
pair<int,int> p = find_zero();
int r = p.first, c = p.second;
if (r == -1) {
// Step 4: generate new zeros
double d = 1e18;
for (int i = 0; i < n; i++) if (!row_cover[i])
for (int j = 0; j < n; j++) if (!col_cover[j])
d = min(d, cost[i][j]);
for (int i = 0; i < n; i++) {
if (!row_cover[i])
for (int j = 0; j < n; j++)
cost[i][j] -= d;
for (int j = 0; j < n; j++)
if (col_cover[j])
cost[i][j] += d;
}
}
else {
mark[r][c] = 2; // prime
int star_col = find_star_in_row(r);
if (star_col == -1) {
// augment path
vector<pair<int,int>> path;
path.push_back(make_pair(r, c));
while (true) {
int star_row = find_star_in_col(path.back().second);
if (star_row == -1) break;
path.push_back(make_pair(star_row, path.back().second));
int prime_col = find_prime_in_row(path.back().first);
path.push_back(make_pair(path.back().first, prime_col));
}
for (auto &pp : path) {
int i = pp.first, j = pp.second;
mark[i][j] = (mark[i][j] == 1 ? 0 : 1);
}
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
if (mark[i][j] == 2) mark[i][j] = 0;
fill(row_cover.begin(), row_cover.end(), false);
fill(col_cover.begin(), col_cover.end(), false);
for (int j = 0; j < n; j++)
for (int i = 0; i < n; i++)
if (mark[i][j] == 1)
col_cover[j] = true;
break;
} else {
row_cover[r] = true;
col_cover[star_col] = false;
}
}
}
}
// 输出匹配结果
vector<int> assign(n, -1);
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
if (mark[i][j] == 1)
assign[i] = j;
return assign;
}
int main()
{
int n = 10;
srand(0);
vector<vector<double>> cost(n, vector<double>(n));
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
cost[i][j] = rand() % 20 + 1;
cout << "代价矩阵:" << endl;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++)
cout << setw(3) << cost[i][j] << " ";
cout << endl;
}
vector<int> assign = hungarian(cost);
double total = 0;
cout << "\n最优匹配结果:" << endl;
for (int i = 0; i < n; i++) {
cout << "行 " << i+1 << " → 列 " << assign[i]+1
<< " , 代价 = " << cost[i][assign[i]] << endl;
total += cost[i][assign[i]];
}
cout << "总代价 = " << total << endl;
return 0;
}
Note
上面介绍的三种匈牙利算法:
- Kuhn 算法
- KM 算法(Kuhn-Munkres)
- Munkres 算法(矩阵匈牙利)
本质上是相同的,都是为了解决最大权重/最小代价的匹配问题。其中,Kuhn 算法(无权图)是 KM 算法(有权图)的一种特殊情形,只需将 KM 算法中权重设置为0、1两个值,就退化为 Kuhn 算法。而 KM 算法和 Munkres 算法等价,是同一个问题的两种实现,前者使用图论方法(顶标、相等子图、松弛),后者使用矩阵方法(行列相减、最小子图覆盖0)。
接下来,介绍完了匈牙利算法这一基本思想,我们正式进入 MOT 中的常用算法。
-
[1]吴楚峥.基于深度学习的单目摄像头人员跟踪定位方法研究[D].西安科技大学,2022.DOI:10.27397/d.cnki.gxaku.2022.001665. ↩