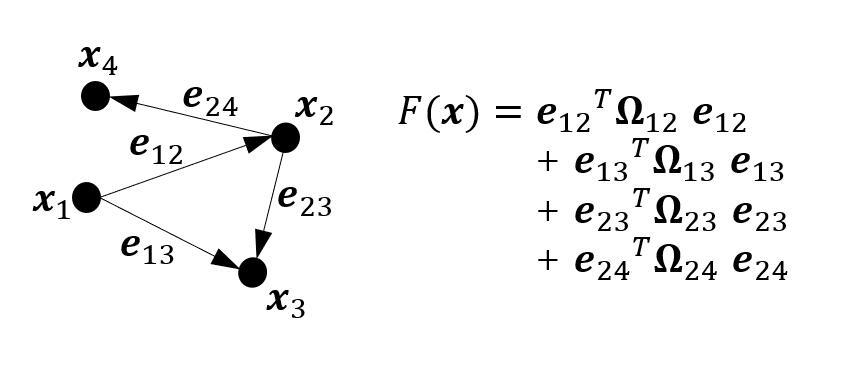Graph Optimization 图优化¶
绪论¶
本章节参考:
SLAM 的处理方法主要有滤波和图优化两种。其中滤波方法是增量式的,在每一时刻处理实时数据并校正机器人的位姿,例如扩展卡尔曼滤波、粒子滤波。图优化方法是存储所有运动过程中的数据,最后统一进行处理。
图由边和节点构成。在 SLAM 中,机器人的整个运动过程构成图,机器人的位姿构成顶点(vertex),位姿之间的关系构成边(edge),例如里程计、IMU、GPS、LiDAR 等传感器的观测约束等。图构建完成后,需要调整顶点(机器人的位姿)以尽量满足这些边构成的约束。
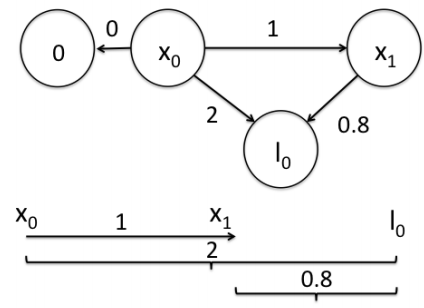
举一个简单的例子:
假设一个机器人初始起点在 0m 处,观测到其正前方 2m 处有一个路标。然后机器人向前移动,通过编码器测得它向前移动了 1m,此时观测到路标在其前方 0.8m。如何求解机器人位姿和路标位姿的最优状态?
我们将路标也看作一个顶点,构建边的关系:
也即:
残差的平方和:
求残差最小值,令其偏导数为0:
得到 \(x_0=0,\;x_1=1.07,\;l_0=1.93\) .
考虑到实际传感器的精度有差别,我们应该更倾向于相信精度更高的传感器,因此可以对不同传感器数据的信任程度赋予不同的权重。例如假设编码器的数据很准确,测量与路标距离的信息误差较大,那么可以赋给编码器数据更高的权重10,其他保持不变,残差变为:
得到 \(x_0=0,\;x_1=1.01,\;l_0=1.9\) . 显然这里估计出来的位姿 \(x_1\) 比之间的结果更加接近编码器的测距 1m。这里不同边的权重就是边的信息矩阵。
理论推导¶
本章节参考:
SLAM 问题可以表述为一个 非线性最小二乘问题:
其中 \(\boldsymbol{x} = \left[\boldsymbol{x}_1^T, \cdots, \boldsymbol{x}_n^T\right]^T \in \mathbb{R}^N\) 为全部参数组成的向量, \(\boldsymbol{x}_k, k = 1, \cdots, n\) 表示一个参数块。 \(C\) 是全部参与求和的参数块组合, \(\boldsymbol{e}_{ij}(\boldsymbol{x}_i, \boldsymbol{x}_j, \boldsymbol{z}_{ij}) \in \mathbb{R}^{M_{ij}}\) 称为误差函数, \(\boldsymbol{\Omega}_{ij} \in \mathbb{R}^{M_{ij} \times M_{ij}}\) 称为信息矩阵,为对称正定矩阵。
注意,这里为方便推导,假定误差函数的自变量是两个参数块,但在实际情况下,误差函数自变量可以仅包含一个参数块,也可以包含更多的参数块,此时该问题的求解方式可以很方便地通过拓展下面的推导得到。
非线性最小二乘问题可以通过图来构建,其中顶点表示参数块,边表示误差函数,此时称之为图优化问题。
略写误差函数中的观测量,并将误差函数视作全部参数的函数,即采用下面的记法:
通过泰勒展开得到误差函数的一阶近似:
其中 \(\boldsymbol{e}_{ij} = \boldsymbol{e}_{ij}(\boldsymbol{x})\) , \(\boldsymbol{J}_{ij} = \displaystyle\lim_{\Delta x \to 0} \frac{\boldsymbol{e}_{ij}(\boldsymbol{x} + \Delta \boldsymbol{x}) - \boldsymbol{e}_{ij}(\boldsymbol{x})}{\Delta \boldsymbol{x}} \in \mathbb{R}^{M_{ij} \times N}\) .
考虑到参数 \(\boldsymbol{x}\) 可能位于非欧式空间 \(\text{Dom}(\boldsymbol{x})\) ,而摄动量 \(\Delta \boldsymbol{x}\) 位于欧式空间 \(\mathbb{R}^N\) ,故上式中的向量加法很可能导致 \(\boldsymbol{x} + \Delta \boldsymbol{x} \notin \text{Dom}(\boldsymbol{x})\) . 例如四维变换矩阵 T 或者三维旋转矩阵 R 对加法并不封闭,两个变换阵之和不是变换阵,两个正交阵之和也不是正交阵。
为解决该问题,可采用广义加法 \(\oplus : \text{Dom}(\boldsymbol{x}) \times \mathbb{R}^N \rightarrow \text{Dom}(\boldsymbol{x})\) 将(7)改写为:
其中 \(\boldsymbol{J}_{ij} = \displaystyle\lim_{\Delta x \to 0} \frac{\boldsymbol{e}_{ij}(\boldsymbol{x} \oplus \Delta \boldsymbol{x}) - \boldsymbol{e}_{ij}(\boldsymbol{x})}{\Delta \boldsymbol{x}} \in \mathbb{R}^{M_{ij} \times N}\) .
记 \(F_{ij}(\boldsymbol{x}_i, \boldsymbol{x}_j, \boldsymbol{z}_{ij}) = \dfrac{1}{2} \boldsymbol{e}_{ij}(\boldsymbol{x}_i, \boldsymbol{x}_j, \boldsymbol{z}_{ij})^T \boldsymbol{\Omega}_{ij} \boldsymbol{e}_{ij}(\boldsymbol{x}_i, \boldsymbol{x}_j, \boldsymbol{z}_{ij})\) ,同样略去误差测量,并将 \(F_{ij}\) 视作全部参数的函数,即采用下面的记法:
计算 \(F_{ij}(\boldsymbol{x} \oplus \Delta \boldsymbol{x})\) :
将(4)代入(1)计算 \(F(\boldsymbol{x} + \Delta \boldsymbol{x})\) :
其中 \(\boldsymbol{b} = \displaystyle\sum_{(\boldsymbol{x}_i, \boldsymbol{x}_j) \in C} \boldsymbol{b}_{ij} \in \mathbb{R}^n\) , \(\boldsymbol{H} = \displaystyle\sum_{(\boldsymbol{x}_i, \boldsymbol{x}_j) \in C} \boldsymbol{H}_{ij} \in \mathbb{R}^{N \times N}\) .
实际上, \(\boldsymbol{b}\) 等于 \(F\) 在 \(\boldsymbol{x}\) 点处的梯度,而采用 \(\boldsymbol{H}\) 近似 \(F\) 在 \(\boldsymbol{x}\) 点处的 Hessian 矩阵:
梯度下降法¶
通过取增量方向为目标函数的负梯度方向,来保证目标函数的一阶近似下降:
保留(5)至一阶项:
此时取
即可保证目标函数的一阶近似下降,其中 \(\lambda > 0\) 称为步长。
梯度下降法求解非线性最小二乘问题的具体步骤如下:
- 令 \(k=0\) ,给定初始值 \(\boldsymbol{x}_0,\;\lambda\) .
- 若 \(k\) 达到最大迭代次数,则停止迭代;否则根据 \(\boldsymbol{x}_k\) 求出当前的和 \(\boldsymbol{b}_k\) .
- 令 \(\Delta \boldsymbol{x}_k = -\lambda \boldsymbol{b}_k\) .
- 如果 \(\Delta \boldsymbol{x}_k\) 足够小,则停止迭代;否则令 \(\boldsymbol{x}_{k+1} = \boldsymbol{x}_k \oplus \Delta \boldsymbol{x}_k,\;k = k + 1\) ,返回第2步。
高斯牛顿法¶
高斯牛顿法采用 \(\boldsymbol{H}\) 近似 \(F(\boldsymbol{x})\) 在 \(\boldsymbol{x}\) 点处的 Hessian 矩阵,避免了 Hessian 矩阵的计算,又可以通过求解二阶近似的最小值实现更快的收敛。
因为 \(\boldsymbol{H}\) 矩阵半正定,故 \(\Delta \boldsymbol{x}\) 的函数 \(F(\boldsymbol{x} \oplus \Delta \boldsymbol{x})\) 为凸函数,因此其最小值在 \(\dfrac{\partial F(\boldsymbol{x} \oplus \Delta \boldsymbol{x})}{\partial \Delta \boldsymbol{x}} = 0\) 处取得,即要求 \(\Delta \boldsymbol{x}\) 满足下式时取得:
上式称为增量方程,求解增量方程是整个优化问题的核心。
高斯牛顿法求解非线性最小二乘问题的具体步骤如下:
- 令 \(k=0\) ,给定初始值 \(\boldsymbol{x}_0\) .
- 若 \(k\) 达到最大迭代次数,则停止迭代;否则根据 \(\boldsymbol{x}_k\) 求出当前的 \(\boldsymbol{H}_k,\;\boldsymbol{b}_k\) .
- 求解增量方程:\(\boldsymbol{H}_k \Delta \boldsymbol{x}_k = -\boldsymbol{b}_k\) . 当 \(\boldsymbol{H}\) 正定时,增量方程可以通过 Cholesky 分解高效求解;当 \(\boldsymbol{H}\) 非正定时,可取 \(\Delta \boldsymbol{x}_k = \Delta \boldsymbol{x}_{k-1}\) .
- 如果 \(\Delta \boldsymbol{x}_k\) 足够小,则停止迭代;否则令 \(\boldsymbol{x}_{k+1} = \boldsymbol{x}_k \oplus \Delta \boldsymbol{x}_k,\;k = k + 1\) ,返回第2步。
核函数¶
引入核函数的原因,是因为 SLAM 中可能给出错误的边。由于变化、噪声等原因,机器人并不能确定它看到的某个路标,就一定是数据库中的某个路标。如果把一条原本不应该加到图中的边给加进去,优化算法试图调整这条边所连接的节点的估计值,使它们顺应这条边的约束。由于这个边的误差非常大,往往会抹平了其他正确边的影响,使优化算法专注于调整一个错误的值。
注意到,当某条边的误差 \(e_{ij}\) 很大时, \(F_{ij}(\boldsymbol{x}) = \boldsymbol{e}_{ij}^T \boldsymbol{\Omega}_{ij} \boldsymbol{e}_{ij}\) 会很大,其梯度 \(\nabla F_{ij}(\boldsymbol{x}) = \boldsymbol{J}_{ij}^T \boldsymbol{\Omega}_{ij} \boldsymbol{e}_{ij}\) 也会很大,而算法会根据梯度更大幅度地调整这条边所连接的节点的估计值,而掩盖这些节点与其他边的关系。
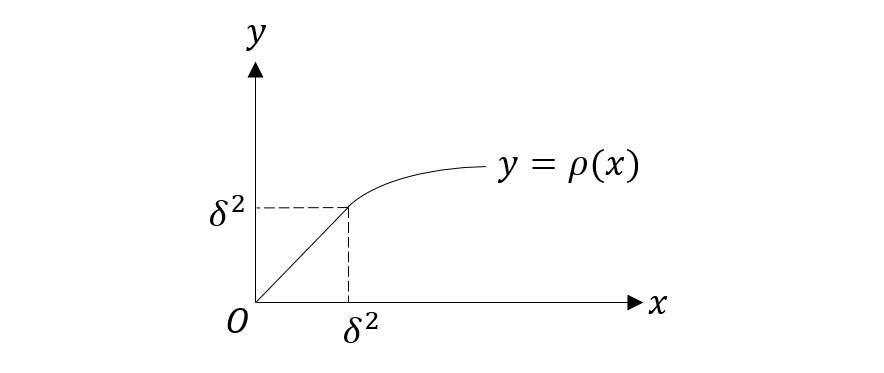
可以定义核函数 \(\rho(\cdot)\) ,在非线性最小二乘问题中用 \(\rho(F_{ij}(\boldsymbol{x}))\) 代替 \(F_{ij}(\boldsymbol{x})\) .
最常用的核函数是 Huber 核函数,其定义为:
Huber 函数图像如下: