第8讲 贝叶斯决策与概率模型

8.1 模式识别

模式 Pattern

1. 模式(认知心理学)：由若干元素或成分按一定关系形成的某种刺激结构。
2. 模式(机器学习)：人们在一定条件环境下，根据一定需要对自然事物的一种抽象的分类概念。模式集合记为 $\Omega=\{\omega_1,\cdots, \omega_C\}$ 。

样本/对象 (sample, object) ：自然界的具体事物，具有一定的类别特性，是抽象模式的具体体现。样本的观测量记为 $\boldsymbol{x}=[x_1,\cdots, x_N]^T$ 。

模式识别：寻求样本观测量与类别属性的联系 $g(\boldsymbol{x})=\omega_i$ 。

特征 Feature：

1. 认知心理学层面：特征是构成模式的元素或成分，以及关系。
2. 机器学习层面：对被识别对象经观察、测量或计算产生的要素。

特征空间：预处理之后分类识别依赖的数据空间。两个概念：特征提取器和模式分类器。

8.2 特征提取与变换

特征变换：降维。

$$\boldsymbol{x}\in \mathbb{R}^p \to \boldsymbol{z}=f(\boldsymbol{x}) \to \boldsymbol{z}\in \mathbb{R}^k,\quad k<p$$

机器学习中的维度灾难：在给定精度下，准确地对某些变量的函数进行估计，所需样本量会随着样本维数的增加而呈指数形式增长。

Quote

如果训练集可以达到理论上的无限个，那么就不存在维度灾难，我们可以用无限个维度去得到一个完美的分类器。训练集样本越少，越应该用少量的特征，如果 $N$ 个训练样本足够覆盖一个一维的特征空间（区间大小为一个单位），那么需要 $N^2$ 个样本去覆盖一个同样密度的二维的特征空间，需要 $N^3$ 个样本去覆盖三维的特征空间。换句话说，就是训练样本多少需要随着维度指数增长。

过拟合：维度增加时，有限的样本空间会越来越稀疏。因此模型出现在训练集上表现良好，但对新数据缺乏泛化能力的现象。

特征降维的意义：克服维数灾难；获取本质特征；节省存储空间；去除无用噪声；实现数据可视化。

由原始特征产生出对分类识别最有效、数目最少的特征，需要保证：同类样本的不变性(Invariant)，异类样本的鉴别性(Discriminative)，对噪声的鲁棒性(Robust)。

特征降维常见方法：特征选择，特征变换。

8.2.1 PCA

主成分分析 PCA (Principal Component Analysis)：Principal component analysis - Wikipedia。

输入数据： $n$ 个 $p$ 维的样本 $\boldsymbol{x}_i\in \mathbb{R}^p$， $i=1,\cdots,n$ 。

目标：寻找最优(方差保留)的 $k$ 个投影方向并进行特征变换降维。

（1）计算样本点 $\boldsymbol{x}_1,\cdots\boldsymbol{x}_n$ 的均值和协方差 $\boldsymbol{\mu},\boldsymbol{\Sigma}$ 。

$$\boldsymbol{\mu}=\frac{1}{n}\sum_{i=1}^n\boldsymbol{x}_i \\ \boldsymbol{\Sigma}=\mathbb{E}[(\boldsymbol{x}-\boldsymbol{\mu})(\boldsymbol{x}-\boldsymbol{\mu})^T] =\frac{1}{n}\sum_{i=1}^n(\boldsymbol{x}_i-\boldsymbol{\mu})(\boldsymbol{x}_i-\boldsymbol{\mu})^T$$

上面求协方差时使用了 去中心化 $\boldsymbol{x}_i=\boldsymbol{x}_i-\boldsymbol{\mu}$ ,也即变为零均值。如果是 无偏估计 ，则 散度矩阵/样本协方差矩阵 变为 $\boldsymbol{\Sigma}=\dfrac{1}{n-1}\displaystyle\sum_{i=1}^n(\boldsymbol{x}_i-\boldsymbol{\mu})(\boldsymbol{x}_i-\boldsymbol{\mu})^T$ 。但实际上，该系数并不会对后面求特征向量造成影响，只是特征值进行了缩放。

关于前面的系数是 1/n 还是 1/(n-1) ，区分不同的场景：最大似然估计的数学推导出来前面是 1/n，这是符合最大似然估计优化原理的理论推导结果。但是在实际用的时候，发现就是这个理论推导的估计有问题，所以重新定义了样本协方差矩阵，前面是 1/(n-1)。简化理解，就是 1/n 是理论推导，1/(n-1) 是实际使用。

（2）对协方差矩阵 $\boldsymbol{\Sigma}$ 进行特征值分解。

（3）选取前 $k$ 个特征值最大的特征向量 $\boldsymbol{v}_1,\cdots,\boldsymbol{v}_k$ 。

（4）将样本点投影到由 $\boldsymbol{v}_1,\cdots,\boldsymbol{v}_k$ 张成的子空间（各个列向量需要归一化）上，得到降维后的样本点 $\boldsymbol{z}_i=\boldsymbol{V}^T(\boldsymbol{x}_i-\boldsymbol{\mu})$ 。

（5）重建： $k$ 维投影子空间内的某个向量 $\boldsymbol{z}$ ，可以重构原始空间的向量 $\tilde{\boldsymbol{x}}=\boldsymbol{V}\boldsymbol{z}+\boldsymbol{\mu}$ 。

应用案例：基于 PCA 变换的人脸识别。

PCA 的几何意义：样本 $\boldsymbol{x}_i,\cdots\boldsymbol{x}_n$ 在 $p$ 维空间中形成一个椭球形云团，散度矩阵/协方差矩阵的特征向量即为椭球状云团的主轴。PCA 提取云团散度最大的主轴方向进行特征降维。

PCA 的优缺点分析：

1. 优点：采用样本协方差矩阵的特征向量作为变换的基向量，与样本的统计特性完全匹配。PCA 在 最小均方误差准则 下是最佳变换。
2. 缺点：变换矩阵随样本数据而异，无快速算法（散度最大不一定最利于区分样本类别）。

---

t-SNE (t-distributed stochastic neighbor embedding)

高维空间: 以数据点在 $x_i$ 为中心的高斯分布中所占概率密度为标准选择近邻：

$$p_{j|i} = \frac{\exp\left(-\|x_i - x_j\|^2 / 2\sigma_i^2\right)}{\displaystyle\sum_{k \neq i} \exp\left(-\|x_i - x_k\|^2 / 2\sigma_i^2\right)} \\ p_{ij} = \frac{p_{i|j} + p_{j|i}}{2N}$$

低维空间: 以 t 分布替代高斯分布表达距离：

$$q_{ij} = \frac{\left(1 + \|y_i - y_j\|^2\right)^{-1}}{\displaystyle\sum_{k \neq l} \left(1 + \|y_k - y_l\|^2\right)^{-1}}$$

优化目标：高维空间和低维空间的概率分布之间距离——KL 散度 (Kullback-Leibler divergences)：

$$C = \sum_i KL(P_i \| Q_i) = \sum_i \sum_j p_{ij} \log \frac{p_{ij}}{q_{ij}}$$

推导 $C$ 对于 $y_i$ 的梯度为：

$$\frac{\partial C}{\partial y_i} = 4 \sum_j (p_{ij} - q_{ij})(y_i - y_j)\left(1 + \| y_i - y_j \|^2\right)^{-1}$$

利用梯度下降求解 $x_i$ 的低维映射 $y_i$ 。

8.3 Bayes Decision

8.3.1 数学基础

条件概率和联合概率：

假设 A 和 B 是一个样本空间中的两个事件，在假定 B 发生的条件下，A 发生的条件概率为：

$$P(A|B) = \frac{P(A,B)}{P(B)}$$

事件 A 和事件 B 的联合概率为：

$$P(A,B) = P(A|B)P(B) = P(B|A)P(A)$$

假设 $A_1$ 和 $A_2$ 是互斥的两个事件，且 $A_1 \cup A_2 = S$ ，事件 $B$ 发生的概率（边际概率）为 全概率公式:

$$P(B) = P(B|A_1)P(A_1) + P(B|A_2)P(A_2)$$

两事件的贝叶斯定理为：

$$P(A_i|B) = \frac{P(A_i)P(B|A_i)}{P(A_1)P(B|A_1) + P(A_2)P(B|A_2)}, \quad i = 1, 2$$

n 事件的贝叶斯定理为：

$$P(A_i|B) = \frac{P(A_i)P(B|A_i)}{\displaystyle\sum_{j=1}^{n} P(A_j)P(B|A_j)}$$

---

两事件的贝叶斯定理为：

$$P(A_i|B) = \frac{P(A_i)P(B|A_i)}{P(B)}, \quad i = 1, 2$$

模式识别中的贝叶斯定理表示：

$$P(\omega_i|x) = \frac{P(\omega_i)P(x|\omega_i)}{P(x)}, \quad i = 1, 2$$

通过观测 $x$ 将先验概率 $P(\omega_i)$ 转化为后验概率 $P(\omega_i|x)$ ，其中 $P(x)$ 是边际概率， $P(x|\omega_i)$ 是似然函数。

贝叶斯定理的核心是“执果索引”，后验概率 = 先验概率 × 似然函数 / 边际概率。

---

贝叶斯决策 Bayes Decision ：在所有相关概率已知的条件下，考虑如何利用已知概率，以最小化误判损失函数为目标来选取最优的类别标记。贝叶斯决策是概率框架下实施决策的基本方法。

8.3.2 正态分布下的贝叶斯决策

假设 类条件概率密度函数 为正态分布：

$$\boldsymbol{x}|\omega_i \sim \mathcal{N}(\boldsymbol{\mu}_i, \boldsymbol{\Sigma}_i) \\ p(\boldsymbol{x}|\omega_i) = \frac{1}{(2\pi)^{d/2}\sqrt{|\boldsymbol{\Sigma}_i|}} \exp \left\{ -\frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu}_i)^T \boldsymbol{\Sigma}_i^{-1} (\boldsymbol{x} - \boldsymbol{\mu}_i) \right\}$$

其中 $\boldsymbol{\mu}_i$ 是类别 $\omega_i$ 的均值向量， $\boldsymbol{\Sigma}_i$ 是类别 $\omega_i$ 的协方差矩阵。

判别函数定义为：

$$G_i(\boldsymbol{x}) = p(\boldsymbol{x}|\omega_i)p(\omega_i)$$

取对数后判别函数为：

$$g_i(\boldsymbol{x}) = -\frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu}_i)^T \boldsymbol{\Sigma}_i^{-1} (\boldsymbol{x} - \boldsymbol{\mu}_i) - \frac{d}{2} \ln(2\pi) - \frac{1}{2} \ln|\boldsymbol{\Sigma}_i| + \ln p(\omega_i)$$

找到所有 $g_i(\boldsymbol{x})$ 的最大值，则判别为类别 $\omega_i$ 。两个类之间的分类判别边界为 $g_i(\boldsymbol{x}) = g_j(\boldsymbol{x})$ 。

对于常见的 二分类问题，分类判别边界为 $g_1(\boldsymbol{x})-g_2(\boldsymbol{x})=0$ ，即：

$$g_1(\boldsymbol{x})-g_2(\boldsymbol{x}) >0 \implies \boldsymbol{x} \in \omega_1 \\ g_1(\boldsymbol{x})-g_2(\boldsymbol{x}) <0 \implies \boldsymbol{x} \in \omega_2$$

假设 各类先验概率相等 $p(\omega_i)=\dfrac{1}{c},\;i=1,\cdots c$ ，协方差矩阵的三种情况：

1. $\boldsymbol{\Sigma}_i = \sigma^2 \boldsymbol{I}$ 最小欧氏距离分类器。协方差矩阵为单位阵的倍数。
2. $\boldsymbol{\Sigma}_i = \boldsymbol{\Sigma}$ 最小马氏距离分类器。所有类别的协方差矩阵相等。
3. $\boldsymbol{\Sigma}_i \neq \boldsymbol{\Sigma}_j,\;i \neq j$ ，二次判别函数。各个类的协方差矩阵各不相同。

下面对这几种情况具体讨论

协方差矩阵相等且为对角阵

假设 样本的特征向量的各个分量独立且具有相同的方差 $\sigma^2$ ，则协方差矩阵为 $\boldsymbol{\Sigma}_i = \sigma^2 \boldsymbol{I},\;i=1,\cdots c$ 。

此时，有 $\| \boldsymbol{\Sigma}_i \|=\sigma^{2d},\; \boldsymbol{\Sigma}_i^{-1}=\dfrac{1}{\sigma^2}\boldsymbol{I},\;i-1,\cdots c$ 。

（1）条件： $\boldsymbol{\Sigma}_i = \sigma^2 \boldsymbol{I},\;p(\omega_i)=\dfrac{1}{c},\;i=1,\cdots c$ 即各类先验概率都相等时，为 最小欧氏距离分类器。

我们 忽略所有与类别无关的常数项，只剩下带协方差矩阵的那一项，得到判别函数：

$$g_i(\boldsymbol{x}) = -\frac{\|\boldsymbol{x} - \boldsymbol{\mu}_i\|^2}{2\sigma^2}$$

其中，欧氏距离的平方： $\|\boldsymbol{x} - \boldsymbol{\mu}_i\|^2 = (\boldsymbol{x} - \boldsymbol{\mu}_i)^T(\boldsymbol{x} - \boldsymbol{\mu}_i)=\displaystyle\sum_{j=1}^d (x_j - \mu_{ij})^2$ 。

判决规则：每个样本 以它到 每类样本均值 的 欧式距离平方的最小值 确定其分类，即：

$$i = \argmin_{j=1,\cdots,c} \|\boldsymbol{x} - \boldsymbol{\mu}_j\|^2 \implies \boldsymbol{x} \in \omega_i$$

各类 $d$ 维球状分布，判决超平面 垂直于 连接两类中心（类别均值向量）的连线。

可看作模板匹配：每个类有一个典型样本(即均值向量)，称为模板；而待分类样本 $\boldsymbol{x}$ 只需按欧氏距离计算与哪个模板最相似(欧氏距离最短)即可作决定。

（2）条件： $\boldsymbol{\Sigma}_i = \sigma^2 \boldsymbol{I},\;p(\omega_i)\neq p(\omega_j)$ 即 各类的先验概率未知，为 线性分类器。

忽略与类别无关的常数项，得到判别函数——线性判别函数 LDF (Linear Discriminant Function)：

$$g_i(\boldsymbol{x}) = -\frac{\|\boldsymbol{x} - \boldsymbol{\mu}_i\|^2}{2\sigma^2} + \ln p(\omega_i) \\ = -\frac{1}{2\sigma^2} \left(\cancel{\color{red}{\boldsymbol{x}^T\boldsymbol{x}}} - 2\boldsymbol{\mu}_i^T \boldsymbol{x} + \boldsymbol{\mu}_i^T\boldsymbol{\mu}_i \right) + \ln p(\omega_i) \\ \Rightarrow \boxed{\boldsymbol{w}_i^T \boldsymbol{x} + b_i} \\ \boldsymbol{w}_i = \frac{1}{\sigma^2} \boldsymbol{\mu}_i, \quad b_i = -\frac{1}{2\sigma^2} \boldsymbol{\mu}_i^T\boldsymbol{\mu}_i + \ln p(\omega_i)$$

判别函数为线性函数，决策面为超平面，决策面向先验概率小的类偏移。

协方差矩阵相等

假设 各类协方差矩阵相等，但不再是前面特殊的对角阵形式，即： $\boldsymbol{\Sigma}_i = \boldsymbol{\Sigma},\;i=1,\cdots c$ 。

（3） 条件： $\boldsymbol{\Sigma}_i = \boldsymbol{\Sigma},\;p(\omega_i)=\dfrac{1}{c},\;i=1,\cdots c$ 即各类先验概率都相等时，为 最小马氏距离分类器。

马氏距离(Mahalanobis distance) $d_M(\boldsymbol{x},\boldsymbol{\mu}_i) = \sqrt{(\boldsymbol{x} - \boldsymbol{\mu}_i)^T \boldsymbol{\Sigma}_i^{-1} (\boldsymbol{x} - \boldsymbol{\mu}_i)}$ 。

判别函数为样本 $\boldsymbol{x}$ 到类均值 $\boldsymbol{\mu}_i$ 的马氏距离的平方 化简为：

$$g_i(\boldsymbol{x}) =-\frac{1}{2}d_M^2 = -\frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu}_i)^T \boldsymbol{\Sigma}^{-1} (\boldsymbol{x} - \boldsymbol{\mu}_i)$$

几何上，具有同样概率密度函数的点的轨迹是同样大小和形状的超椭球面，中心由类均值 $\boldsymbol{\mu}_i$ 决定。

各类 $d$ 维椭球状分布，判决超平面通过两类中心的中点，但未必垂直于连接两类中心的连线。

（4）条件： $\boldsymbol{\Sigma}_i = \boldsymbol{\Sigma},\;p(\omega_i)\neq p(\omega_j)$ 即各类的先验概率未知，仍然为 线性分类器。

$$g_i(\boldsymbol{x}) = -\frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu}_i)^T \boldsymbol{\Sigma}^{-1} (\boldsymbol{x} - \boldsymbol{\mu}_i) + \ln p(\omega_i) \\ =-\frac{1}{2}\left(\cancel{\color{red}{\boldsymbol{x}^T\boldsymbol{\Sigma}^{-1}\boldsymbol{x}}} - 2\boldsymbol{\mu}_i^T \boldsymbol{\Sigma}^{-1} \boldsymbol{x} + \boldsymbol{\mu}_i^T\boldsymbol{\Sigma}^{-1}\boldsymbol{\mu}_i \right) \boldsymbol{\Sigma}^{-1} + \ln p(\omega_i) \\ =\boxed{\boldsymbol{w}_i^T \boldsymbol{x} + b_i} \\ \boldsymbol{w}_i = \boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}_i, \quad b_i = -\frac{1}{2} \boldsymbol{\mu}_i^T \boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}_i + \ln p(\omega_i)$$

判别函数为线性函数，决策面为超平面，决策面向先验概率小的类偏移。

协方差矩阵不相等

最一般的情况。

（5）当 $\boldsymbol{\Sigma}_i \neq \boldsymbol{\Sigma}_j,\;i \neq j$ 各个类的协方差矩阵都不相同。

忽略与判别函数无关的常数项，得到判别函数——二次判别函数 QDF (Quadratic Discriminant Function)

$$g_i(x)=-\frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu}_i)^T \boldsymbol{\Sigma}_i^{-1} (\boldsymbol{x} - \boldsymbol{\mu}_i) + \ln p(\omega_i) - \frac{1}{2}\ln|\boldsymbol{\Sigma}_i| \\ =\boxed{\boldsymbol{x}^T\boldsymbol{W}_i\boldsymbol{x} + \boldsymbol{w}_i^T\boldsymbol{x} + b_i} \\ \boldsymbol{W}_i = -\frac{1}{2} \boldsymbol{\Sigma}_i^{-1}, \quad \boldsymbol{w}_i = \boldsymbol{\Sigma}_i^{-1} \boldsymbol{\mu}_i, \quad b_i = -\frac{1}{2} \boldsymbol{\mu}_i^T \boldsymbol{\Sigma}_i^{-1} \boldsymbol{\mu}_i + \ln p(\omega_i) - \frac{1}{2}\ln|\boldsymbol{\Sigma}_i|$$

判别函数是关于 $\boldsymbol{x}$ 的二次型，决策面为二次超曲面，可能是超球面、超椭球面、超抛物面、超双曲线或超平面。

上述部分内容参考 贝叶斯决策理论 和 模式识别（贝叶斯决策）。

8.4 参数估计方法

频率学派和贝叶斯学派：

• 相同点：最大似然函数 在频率学派和贝叶斯学派都具有重要的作用，其思想是认为已观测数据的概率分布是最大概率，最大概率对应的模型就是需要找的模型，“存在即合理”。
• 不同点：频率学派认为模型是一成不变的，即 模型参数是常数，常使用的参数估计方法为 极大似然估计 MLE；贝叶斯学派认为模型是一直在变的，当获取新的信息后，模型也相应的在改变，即 模型参数是变量，用概率去描述模型参数的不确定性，常使用的参数估计方法为 最大后验概率估计 MAP。

8.4.1 MLE

最大似然估计 MLE (Maximum Likelihood Estimation)：已知随机变量属于某种概率分布的前提下，利用随机变量的观测值，估计出分布的一些参数值。即：“模型已定，参数未知”。

关键假设：样本值是 独立同分布 的。

最大似然估计：

$$l(\theta) \equiv \ln p(D|\theta) = \sum_{i=1}^{n} \ln p(x_i|\theta) \\ \hat{\theta} = \arg \max_{\theta} l(\theta)$$

其中 $\theta$ 是模型参数，为标量或向量，具体取决于模型。 $D$ 是观测数据， $x_i$ 是第 $i$ 个观测样本。

高斯分布假设的最大似然估计：

$$\hat{\boldsymbol{\mu}} = \hat{\boldsymbol{\theta}}_1 = \frac{1}{n} \sum_{k=1}^{n} \boldsymbol{x}_k \\ \hat{\boldsymbol{\Sigma}} = \hat{\boldsymbol{\theta}}_2 = \frac{1}{n} \sum_{k=1}^{n} (\boldsymbol{x}_k - \hat{\boldsymbol{\mu}})(\boldsymbol{x}_k - \hat{\boldsymbol{\mu}})^T$$

无偏估计样本 的 协方差矩阵：

$$C = \frac{1}{n-1} \sum_{k=1}^{n} (x_k - \hat{\mu})(x_k - \hat{\mu})^T$$

8.4.2 MAP

最大后验估计 MAP (Maximum A Posteriori Estimation)：给定模型形式和参数的先验分布，根据数据，找到在数据和先验下最可能的参数。

在给定数据样本的情况下，最大化模型参数的后验概率。根据已知样本，来通过调整模型参数使得模型能够产生该数据样本的概率最大，只不过对于模型参数有了一个先验假设，即模型参数可能满足某种分布，不再一味地依赖数据。参考自 极大似然估计与最大后验概率估计 - 知乎。

最大后验概率估计可以从最大似然估计推导出来。

最大后验的实质就是对参数的每一个可能的取值，都进行极大似然估计，并根据这个取值可能性的大小，设置极大似然估计的权重，然后选择其中最大的一个，作为最大后验估计的结果。参考自 最大后验（Maximum a Posteriori，MAP）概率估计详解_最大后验概率-CSDN博客。

最大后验估计：

$$l(\theta) = \ln p(D|\theta) = \sum_{i=1}^{n} \ln p(\boldsymbol{x}_i|\theta) \\ \hat{\theta} = \arg \max_{\theta} l(\theta) + \ln p(\theta)$$

高斯分布假设的最大后验估计（均值未知）：

$$\boldsymbol{\mu}_n = \boldsymbol{\Sigma}_0 \left( \frac{1}{n} \boldsymbol{\Sigma} + \boldsymbol{\Sigma}_0 \right)^{-1} \left( \frac{1}{n} \sum_{k=1}^{n} \boldsymbol{x}_k \right) + \frac{1}{n} \boldsymbol{\Sigma} \left( \frac{1}{n} \boldsymbol{\Sigma} + \boldsymbol{\Sigma}_0 \right)^{-1} \boldsymbol{\mu}_0 \\ \boldsymbol{\Sigma}_n = \boldsymbol{\Sigma}_0 \left( \frac{1}{n} \boldsymbol{\Sigma} + \boldsymbol{\Sigma}_0 \right)^{-1} \frac{1}{n} \boldsymbol{\Sigma}$$

其中 $\boldsymbol{\mu}_0$ 是先验均值向量， $\boldsymbol{\Sigma}_0$ 是先验协方差矩阵， $\boldsymbol{\Sigma}$ 是样本协方差矩阵。计算得出的 $\boldsymbol{\mu}_n,\;\boldsymbol{\Sigma}_n$ 分别是后验均值向量和后验协方差矩阵。

8.4.3 GMM

混合高斯模型 GMM (Gaussian Mixture Model)

混合高斯模型比高斯模型具有更强的描述能力，但其需要的参数也成倍增加，实际中通常对节点方差矩阵结构进行约束：

$$p(\boldsymbol{x}|\omega) = \sum_{k=1}^{K} \pi_k \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k), \quad \sum_{k=1}^{K} \pi_k = 1$$

混合分布的概率密度估计问题：

所有样本都来自于 $K$ 种类别，且 $K$ 已知，样本类别未被标记。每种类别的先验概率 $p(\omega_i)$ 未知，类条件概率的数学形式已知 $p(\boldsymbol{x}|\omega_i,\boldsymbol{\theta}_i)$ 但参数 $\boldsymbol{\theta}_i$ 未知。

$$p(\boldsymbol{x}|\boldsymbol{\theta}) = \sum_{i=1}^{K} p(\boldsymbol{x}|\omega_i,\boldsymbol{\theta}_i)p(\omega_i) = \sum_{i=1}^{K} \pi_i \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_i, \boldsymbol{\Sigma}_i)$$

混合高斯分布一共有 $K$ 个分布，并且对于每个观察到的 $\boldsymbol{x}$ ，如果我们同时还知道它属于 $1\sim K$ 中的哪一种分布，则我们可以根据 最大似然估计 求出每个参数。观察数据 $\boldsymbol{x}$ 属于哪个高斯分布是未知的，这时需要采用 EM 算法。

EM 算法 应用于 混合高斯模型参数估计

期望最大值 EM 算法：

给定一些观察数据 $\boldsymbol{x}$，假设 $\boldsymbol{x}$ 符合如下混合高斯分布： $p(x)=\displaystyle\sum_{k=1}^{K} \pi_k \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)$ 。求混合高斯分布的参数 $\boldsymbol{\theta}=\{\pi_k,\boldsymbol{\mu}_k,\boldsymbol{\Sigma}_k\}$ 的最大似然估计。

（1）初始化 $K$ 个高斯分布参数 $\boldsymbol{\mu}_k, \boldsymbol{\Sigma_k}$，初始化 $\pi_k$ 并保证 $\displaystyle\sum_{k=1}^{K} \pi_k = 1$

（2）依据目前的高斯分布参数，对样本 $\boldsymbol{x}$ 的类别隐藏变量 $z_{nk}$ 求 期望，则 $\gamma(z_{nk})$ 表示第 $n$ 个样本 $\boldsymbol{x}_n$ 属于第 $k$ 类的概率：

$$\gamma(z_{nk}) = \frac{\pi_k \mathcal{N}(\boldsymbol{x}_n|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)}{\displaystyle\sum_{j=1}^{K} \pi_j \mathcal{N}(\boldsymbol{x}_n|\boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j)}$$

（3）对高斯分布参数 求最大似然估计：

$$\boldsymbol{\mu}_k^{\text{new}} = \frac{1}{N_k} \sum_{n=1}^{N} \gamma(z_{nk}) \boldsymbol{x}_n \\ \boldsymbol{\Sigma}_k^{\text{new}} = \frac{1}{N_k} \sum_{n=1}^{N} \gamma(z_{nk})(\boldsymbol{x}_n - \boldsymbol{\mu}_k^{\text{new}})(\boldsymbol{x}_n - \boldsymbol{\mu}_k^{\text{new}})^T \\ \pi_k^{\text{new}} = \frac{N_k}{N} ,\quad N_k = \sum_{n=1}^{N} \gamma(z_{nk})$$

（4）迭代计算第2、3步，直到满足参数收敛条件或停止条件。

8.4.4 HMM

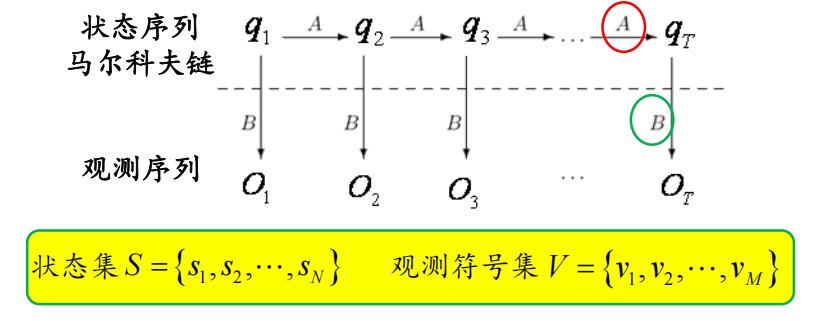
隐含马尔可夫模型 HMM (Hidden Markov Model)

数学基础

（复习随机过程时间到😂）

假设 $Q = (q_1, q_2, \cdots, q_T)$ 是一取值于有限集合 $S = \{s_1, s_2, \cdots, s_N\}$ 的随机变量序列，满足：

$$P(q_{t+1} = s_k | q_1, q_2, \cdots, q_t) = P(q_{t+1} = s_k | q_t)$$

则称序列 $Q$ 具有 Markov 性，为 Markov 链。

若进一步满足 $P(q_{t+1} = s_k | q_t) = P(q_2 = s_k | q_1)$，则称序列 $Q$ 是齐次 Markov 链。

齐次 Markov 链可以用状态转移概率矩阵 $\boldsymbol{A}$ 和初始概率 $\boldsymbol{\pi}$ 唯一确定表示：

$$\boldsymbol{A} = \{a_{ij}\} \\ a_{ij} = p(q_{t+1} = s_j | q_t = s_i), \quad a_{ij} \geqslant 0, \quad \sum_{j=1}^{N} a_{ij} = 1, \forall i \\ \pi_i = P(q_1 = s_i), \quad \sum_{i=1}^{N} \pi_i = 1$$

隐含马尔可夫模型 HMM 是一个双重随机过程：

• 状态序列：是马尔可夫链，用转移概率描述。
• 观测序列：是一般随机过程，每一状态对应一个可以观察的事件，用观测概率描述。

状态集 $S=\{s_1,s_2,\cdots,s_N\}$ ，即有 $N$ 个不同状态。

观测符号集 $V=\{v_1,v_2,\cdots,v_M\}$ ，即有 $M$ 种不同的观测符号。

观测集 $O=\{o_1,o_2,\cdots,o_T\},o_i\in V$ 。

状态转移概率矩阵 $\boldsymbol{A}\in\mathbb{R}^{N\times N}$ ，其中 $a_{ij}$ 表示从第 $i$ 个状态 $s_i$ 转移到第 $j$ 个状态 $s_j$ 的概率。

观测概率矩阵 $\boldsymbol{B}\in\mathbb{R}^{N\times M}$ ，其中 $b_{ij}$ 表示在第 $i$ 个状态 $s_i$ 下，观测到第 $j$ 个符号 $v_j$ 的概率。

初始状态概率向量 $\boldsymbol{\pi}\in\mathbb{R}^{1\times N}$ ，初始状态下位于第 $i$ 个状态 $s_i$ 的概率为 $\pi_i$ 。

在齐次马尔科夫条件下，某一时刻 $t$ 的状态向量为 $\boldsymbol{\pi}\boldsymbol{A}^t$ 。

HMM 的基本元素：用三元组 $\lambda = (\boldsymbol{\pi},\boldsymbol{A},\boldsymbol{B})$ 来描述：

$$\boldsymbol{A} = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1N} \\ a_{21} & a_{22} & \cdots & a_{2N} \\ \vdots & \vdots & \ddots & \vdots \\ a_{N1} & a_{N2} & \cdots & a_{NN} \end{bmatrix} ,\; \boldsymbol{B} = \begin{bmatrix} b_{11} & b_{12} & \cdots & b_{1M} \\ b_{21} & b_{22} & \cdots & b_{2M} \\ \vdots & \vdots & \ddots & \vdots \\ b_{N1} & b_{N2} & \cdots & b_{NM} \end{bmatrix} ,\; \boldsymbol{\pi} = [\pi_1, \cdots, \pi_N]$$

Note

注意 $\boldsymbol{\pi}$ 是 行向量！矩阵 $\boldsymbol{A},\,\boldsymbol{B}$ 均满足 行和为1。

参数	含义	实例
$\boldsymbol{A}$	与时间无关的状态转移概率矩阵	类间转移概率
$\boldsymbol{B}$	给定状态下，观察值概率分布	给定类别，特征向量分布
$\boldsymbol{\pi}$	初始状态空间的概率分布	初始时选择类别的概率

HMM 的基本假设：

1. 马尔可夫性： $P(q_{t+1} | q_t, \cdots, q_1) = P(q_{t+1} | q_t)$ 。
2. 齐次性，状态转移概率与具体时刻无关： $P(q_{t+1} | q_t ) = P(q_{\tau+1} | q_{\tau })$，对任意 $t,\tau$ 成立。
3. 观测序列独立性： $P(O_1, \cdots, O_T | q_1, \cdots, q_T) = \prod_{t=1}^{T} P(O_t | q_t)$ 。

HMM 的3个基本问题：

1. 评估 问题：
   • 如何根据给定 $O = \{O_1, O_2, \cdots, O_T\}$和 $\lambda$ 计算 $P(O|\lambda)$ ？
   • 即：模型参数 $\lambda$ 已知，评估观测序列 $O$ 出现的概率。
2. 解码 问题：
   • 如何根据给定的 $O,\,\lambda$ 计算最优路径 $Q^*$ ？
   • 即：模型参数 $\lambda$ 和观测序列 $O$ 已知，预测最可能出现的状态序列 $Q^*$ 。
3. 学习 问题：
   • 如何根据观测序列样本集合 $O_{\text{train}}$ 进行模型 $\lambda$ 的参数估计？
   • 即：给定观测序列的集合，训练模型参数，使得 $P(O_{\text{train}}|\lambda)$ 最大化。

评估观测序列的概率

如何根据给定 $O = \{O_1, O_2, \cdots, O_T\}$和 $\lambda$ 计算 $P(O|\lambda)$ ？如何根据给定 $O = \{O_1, O_2, \cdots, O_T\}$和 $\lambda$ 计算 $P(O|\lambda)$ ？

即：模型参数 $\lambda$ 已知，评估观测序列 $O$ 出现的概率。

---

（1）直接计算方法

直接计算可能的状态序列及相应观测值概率。

$P(O|\lambda) = \displaystyle\sum_{Q} P(O,Q|\lambda) = \displaystyle\sum_{Q} P(O|Q,\lambda)P(Q|\lambda)$

$P(O|Q,\lambda) = \displaystyle\prod_{t=1}^{T} P(O_t|q_t, \lambda) = b_{q_1}(O_1) \cdots b_{q_T}(O_T)$

$P(Q|\lambda) = \pi_{q_1} a_{q_1q_2} \cdots a_{q_{T-1}q_T}$

$P(O,Q|\lambda) = P(O|Q,\lambda)P(Q|\lambda)$

$P(O|\lambda) = \displaystyle\sum_{Q} P(O|Q,\lambda)P(Q|\lambda) = \displaystyle\sum_{q_1,\cdots,q_T} \pi_{q_1} b_{q_1}(O_1) a_{q_1q_2} b_{q_2}(O_2) \cdots a_{q_{T-1}q_T} b_{q_T}(O_T)$

计算复杂度为 $O(TN^T)$ 。

---

（2）前向计算法

定义 前向变量：$\alpha_t(i) = P(O_1, \cdots O_t, q_t = s_i | \lambda) ,\; 1\leqslant i \leqslant N,\,1 \leqslant t \leqslant T$ 。表示 $t$ 时刻由第 $i$ 个状态 $s_i$ 生成观测 $O_t$ 且前时刻序列为 $O_1, \cdots, O_{t-1}$ 的概率。这里 $\boldsymbol{\alpha}\in\mathbb{R}^{N}$ 是一个列向量，它的下表 $t$ 代表时刻，括号里的 $i$ 代表元素的位置索引。

我认为更规范更合理的表达方式是 $\boldsymbol{\alpha}^{(t)}\in\mathbb{R}^{N}$ ，每一个前向变量表示为 $\alpha^{(t)}_i \in \mathbb{R}$ 。

同理 $\alpha^{(t+1)}_j = P(O_1, \cdots O_{t+1}, q_{t+1} = s_j | \lambda)$ 表示 $t+1$ 时刻由第 $j$ 个状态 $s_j$ 生成观测 $O_{t+1}$ 且前时刻序列为 $O_1, \cdots, O_t$ 的概率。

$$\alpha^{(t+1)}_j = \sum_{i=1}^{N} \boxed{\color{blue}P(O_1, \cdots O_t, q_t = s_i | \lambda)} \cdot \boxed{\color{red}P(q_{t+1} = s_j | q_t = s_i, \lambda)} \cdot \boxed{\color{green}P(O_{t+1} | q_{t+1} = s_j, \lambda)} \\ =\left[ \sum_{i=1}^{N} {\color{blue}\alpha^{(t)}_i} {\color{red}a_{ij}} \right] {\color{green}b_j(O_{t+1})},\;1 \leqslant j \leqslant N,\;1 \leqslant t \leqslant T-1$$

上式中，蓝色部分即为前向变量 $\alpha^{(t)}_i$ ，红色部分为状态转移概率 $a_{ij}$ （利用到齐次马尔可夫性质），绿色部分为序列下一个观测值的观测概率 $b_j(O_{t+1})$ （利用到观测序列的独立性），也即观测概率矩阵 $\boldsymbol{B}$ 中第 $j$ 行、状态 $O_{t+1}$ 对应的那一列的元素。

具体算法步骤：

(Ⅰ) 初始化： $\alpha^{(1)}_i = \pi_i b_i(O_1) ,\; 1 \leqslant i \leqslant N$ ，表示在 $t=1$ 时刻由第 $i$ 个状态生成观测 $O_1$ 的概率。这样计算出的向量 $\boldsymbol{\alpha}^{(1)}$ ，相当于初态 $\boldsymbol{\pi}$ 和 $\boldsymbol{B}(O_1)$ 列向量进行 逐元素相乘 $\boldsymbol{\alpha}^{(1)} =\left( \boldsymbol{\pi}^T \odot \boldsymbol{B}[:,O_1] \right)$ 。

(Ⅱ) 递归：对于 $t=1, \cdots, T-1$，计算：

$$\alpha^{(t+1)}_j = \left[ \sum_{i=1}^{N} \alpha^{(t)}_i a_{ij} \right] b_j(O_{t+1}), \quad 1 \leqslant j \leqslant N,\; 1 \leqslant t \leqslant T-1$$

上式中，中括号内部分 $\left[ \displaystyle\sum_{i=1}^{N} \alpha^{(t)}_i a_{ij} \right]$ 将计算结果汇总起来后可以发现，实际上是做了这样一个矩阵相乘操作 $\boldsymbol{A}^T\boldsymbol{\alpha}^{(t)}$ ，仍然返回一个列向量 $\in\mathbb{R}^N$ 。然后再与 $\boldsymbol{B}$ 中第 $j$ 行、状态 $O_{t+1}$ 对应的那一列的元素进行逐元素相乘，因此迭代过程实际上是进行了如下运算：

$$\boldsymbol{\alpha}^{(t+1)} = \left(\boldsymbol{A}^T\boldsymbol{\alpha}^{(t)} \right) \odot \boldsymbol{B}[:, O_{t+1}]$$

(Ⅲ) 终止：计算观测序列的总概率 $P(O|\lambda) = \displaystyle\sum_{i=1}^{N} \alpha^{(T)}_i$ ，即为前向向量 $\boldsymbol{\alpha}^{(T)}$ 所有元素之和。

---

（3）后向计算法

类似于前向计算法，我们还将后向向量写成 $\boldsymbol{\beta}^{(t)}$ 的形式，与课件中不同。

定义 后向变量：$\beta^{(t)}_i = P(O_{t+1}, \cdots, O_T | q_t = s_i, \lambda) ,\; 1\leqslant i \leqslant N,\,1 \leqslant t \leqslant T$ 。表示 $t$ 时刻由第 $i$ 个状态 $s_i$ 生成观测序列 $O_{t+1}, \cdots, O_T$ 的概率。

同理有 $\beta^{(t+1)}_j = P(O_{t+2}, \cdots, O_T | q_{t+1} = s_j, \lambda), 1\leqslant t \leqslant T-1$ 表示 $t+1$ 时刻由第 $j$ 个状态 $s_j$ 生成观测序列 $O_{t+2}, \cdots, O_T$ 的概率。

$$\beta^{(t)}_i = \sum_{j=1}^{N} \boxed{\color{blue}P(O_{t+2}, \cdots O_T| q_{t+1} = s_j, \lambda)} \cdot \boxed{\color{red}P(q_{t+1} = s_j | q_t = s_i, \lambda)} \cdot \boxed{\color{green}P(O_{t+1} | q_{t+1} = s_j, \lambda)} \\ = \sum_{j=1}^{N} {\color{blue}\beta^{(t+1)}_j} {\color{red}a_{ij}} {\color{green}b_j(O_{t+1})},\;1 \leqslant j \leqslant N,\;1 \leqslant t \leqslant T-1$$

上式中，蓝色部分即为后向变量 $\beta^{(t+1)}_j$ ，红色部分为状态转移概率 $a_{ij}$ （利用到齐次马尔可夫性质），绿色部分为序列下一个观测值的观测概率 $b_j(O_{t+1})$ （利用到观测序列的独立性），也即观测概率矩阵 $\boldsymbol{B}$ 中第 $j$ 行、状态 $O_{t+1}$ 对应的那一列的元素。

具体算法步骤：

(Ⅰ) 初始化： $\boldsymbol{\beta}^{(T)}=\boldsymbol{1}^{N\times 1}$ ，初值全部为 $1$ 。

(Ⅱ) 递归： $\beta^{(t)}_i = \displaystyle\sum_{j=1}^{N}\beta^{(t+1)}_j a_{ij} b_j(O_{t+1}), \quad 1 \leqslant i \leqslant N,\; 1 \leqslant t \leqslant T-1$ 。相当于做矩阵运算：

$$\boldsymbol{\beta}^{(t)}=\boldsymbol{A}\left(\boldsymbol{\beta}^{(t+1)}\odot \boldsymbol{B}[:,O_{t+1}]\right)$$

(Ⅲ) 终止： $P(O|\lambda) = \displaystyle\sum_{i=1}^{N} \pi_i b_i(O_1) \beta^{(1)}_i$ ，相当于做了逐元素相乘 + 内积运算：

$$P(O|\lambda) = \boldsymbol{\pi}^T \left( \boldsymbol{\beta}^{(1)} \odot \boldsymbol{B}[:,O_1] \right)$$

上面的矩阵运算简化形式经过编写 MATLAB 程序验证是正确的。

解码最佳状态序列

如何根据给定的 $O,\,\lambda$ 计算最优路径 $Q^*$ ？

即：模型参数 $\lambda$ 和观测序列 $O$ 已知，预测最可能出现的状态序列 $Q^*$ 。

联合似然概率最大化：每一时刻状态序列出现相应观测值的可能达到最大

$$\max_{q_1, q_2, \cdots, q_T} P(q_1, q_2, \cdots, q_T, O_1, O_2, \cdots, O_T | \lambda)$$

我们使用 Viterbi 算法：动态规划

思想：记录 $t$ 时刻出现状态 $i$ 的最大可能路径及其对应概率，称为 最大局部概率：

$$\delta^{(t)}_i = \max_{q_1, q_2, \cdots, q_{t-1}} P(q_1, q_2, \cdots, q_t = i, O_1, O_2, \cdots, O_t | \lambda)$$

记 $\varphi^{(t)}_j$ 代表 $t$ 时刻为第 $j$ 个状态时，对应前一时刻 $t-1$ 的状态，与 $O_t$ 无关。

具体算法步骤：

(Ⅰ) 初始化： $\delta^{(1)}_i=\pi_i b_i(O_1),\;\varphi^{(1)}_i=0,\; 1\leqslant i \leqslant N$ 。

其中第一步 相当于 做逐元素相乘操作 $\boldsymbol{\delta}^{(1)} =\left( \boldsymbol{\pi}^T \odot \boldsymbol{B}[:,O_1] \right)$ 以及 $\boldsymbol{\varphi}^{(1)}=\boldsymbol{0}^{N\times 1}$ 。

初始时刻，路径尚未开始，节点局部概率 为 初始时刻在状态 $i$ 发射观测符号 $O_1$ 的概率。

(Ⅱ) 递归：对于 $t=2,3,\cdots,T$，计算：

$$\delta^{(t)}_j = \max_{1\leq i \leq N} \left[ \delta^{(t-1)}_i a_{ij} \right] b_j(O_t) ,\; 1\leqslant j \leqslant N \\ \varphi^{(t)}_j = \argmax_{1\leq i \leq N} \left[ \delta^{(t-1)}_i a_{ij} \right] ,\; 1\leqslant j \leqslant N$$

其中第一步 相当于向量与矩阵逐元素相乘 $\boldsymbol{\delta}^{(t-1)}\boldsymbol{A}$ （把矩阵看作多个列向量，分别与同一个列向量主元素相乘，组成一个新的矩阵），然后 每一列 取最大值得到一个行向量 $\max\left( \boldsymbol{\delta}^{(t-1)}\boldsymbol{A} \right) \in\mathbb{R}^{1\times N}$ ，取转置 变为列向量 之后再和 $\boldsymbol{B}[:,O_t] \in\mathbb{R}^N$ 列向量 做逐元素相乘，得到 $\boldsymbol{\delta}^{(t)}$ 。因此简化为矩阵运算形式：

$$\boldsymbol{\delta}^{(t)} = \left( \max \boldsymbol{\delta}^{(t-1)}\boldsymbol{A} \right)^T \odot \boldsymbol{B}[:, O_t]$$

而 $\boldsymbol{\varphi}^{(t)}$ 就是在寻找矩阵 $\boldsymbol{\delta}^{(t-1)}\boldsymbol{A}$ 中每一列最大值时，那个最大值在其 列向量 中的索引。

转移概率 $a_{ij}$ 与上一步的最大局部概率 $\delta^{(t-1)}_i$ 相乘，记录其中最大的一个。

如果最优路径在 $t$ 时刻到达节点 $j$ ，则从起始时刻到达到该节点的最优路径对应 $\delta^{(t-1)}_i$ 和 $a_{ij}$ 乘积的最小值，并包含从 $1$ 到 $t-1$ 的到达节点 $i$ 的最优路径。

(Ⅲ) 终止： $P^*=\displaystyle\max_{1\leq i \leq N} \delta^{(T)}_i ,\; q^*_T = \displaystyle\argmax_{1\leq i \leq N} \delta^{(T)}_i$ ，得到 $t=T$ 时刻的最大局部概率 $P^*$ 及其对应状态 $q^*_T$ 。

(Ⅳ) 回溯：从 $q^*_T$ 开始， $q^*_t=\boldsymbol{\varphi}_{t+1}(q^*_{t+1}),\;t=T-1,T-2,\cdots 1$ 向前回溯，得到最优路径 $Q^* = (q^*_1, \cdots, q^*_T)$ 。

$\delta^{(T)}_i$ 对应最大值 即为 全局最优路径 $Q^*$ 出现的概率，即为联合似然概率最大值。 $q^*_T$ 为最优路径在 $T$ 时刻状态，结合 $\boldsymbol{\varphi}$ 从 $T-1$ 时刻反向推演到 $1$ 时刻可以获取最优路径。

学习模型参数问题

如何根据观测序列样本集合 $O_{\text{train}}$ 进行模型 $\lambda=(\boldsymbol{\pi},\boldsymbol{A},\boldsymbol{B})$ 的参数估计？

即：给定观测序列的集合，训练模型参数 $\lambda$ ，使得 $P(O_{\text{train}}|\lambda)$ 最大化。

Baum-Welch 算法是一种 EM 算法，是一种从不完全数据（样本特征序列与隐含状态序列的对齐关系未知）求解模型参数的最大似然估计方法：

(Ⅰ)初始化 HMM 参数 $\lambda_0$ ；

(Ⅱ) E 步(Expectation)：利用给定的 HMM 参数求样本特征序列的状态对齐结果；

(Ⅲ) M 步(Maximization)：根据上一步的状态对齐结果，利用最大似然估计更新 HMM 参数 $\lambda$ ；

(Ⅳ) 重复 E 步、M 步，直到算法收敛： $\log P(O|\lambda_{t+1}) - \log P(O|\lambda_t) < \text{threshold}$ 。

给定模型 $\lambda$ 和观测序列 $O$ 的条件下：

首先利用前面定义过的 前向变量和后向变量：

$\alpha_t(i) = P(O_1, \cdots, O_t, q_t = s_i | \lambda)$

$\beta_t(i) = P(O_{t+1}, O_{t+2} \cdots O_T | q_t = s_i, \lambda)$

定义从状态 $i$ 到 $j$ 的转移概率：

$$\xi_t(i,j) = P(q_t = i, q_{t+1} = j | O, \lambda) \\ = \frac{\alpha_t(i) a_{ij} b_j(O_{t+1}) \beta_{t+1}(j)} {\displaystyle\sum_{i=1}^{N} \displaystyle\sum_{j=1}^{N} \alpha_t(i) a_{ij} b_j(O_{t+1})\beta_{t+1}(j)}$$

$\gamma_t(i) = \displaystyle\sum_{j=1}^{N} \xi_t(i,j) = P(q_t = i | O, \lambda)$ 表示 $t$ 时刻处于状态 $s_i$ 的概率。

$\displaystyle\sum_{t=1}^{T-1} \gamma_t(i)$ 表示整个过程中从状态 $s_i$ 转出的次数的预期。

$\displaystyle\sum_{t=1}^{T-1} \xi_t(i,j)$ 表示整个过程中从状态 $s_i$ 跳转至状态 $s_j$ 的次数的预期。

则 模型参数的重估公式 为：

$$\hat{a}_{ij} = \frac{\text{expected count of transitions from } i \text{ to } j}{\text{expected count of stays at } i} = \frac{\displaystyle\sum_t \xi_t(i,j)}{\displaystyle\sum_t \displaystyle\sum_j \xi_t(i,j)} \\ \hat{b}_j(k) = \frac{\text{expected number of times in state } j \text{ and observing } k}{\text{expected number of times in state } j} = \frac{\displaystyle\sum_{t, O_t = k} \gamma_t(j)}{\displaystyle\sum_t \gamma_t(j)}$$

$\hat{\pi}_i=\gamma_1(i)$ ，表示 $t=1$ 时刻处于第 $i$ 个状态 $s_i$ 的概率。

直观理解：利用从状态 $i$ 转移到状态 $j$ 的频次作为 $a_{ij}$ 的估计值；利用从状态 $j$ 产生观测 $k$ 的频次作为 $b_{jk}$ 的估计值。

---

HMM 的应用：

基于 GMM-HMM 的语音识别。

手写文字识别。

2D/3D Talking Head.

8.5 系统及性能评测

8.5.1 模式识别系统

模式识别系统的结构：

输入 → 传感器 → 分割器 → 特征提取器 → 分类器 → 后处理器 → 输出

（1）传感器

例如：摄像机、麦克风阵列传感器。

因素：带宽、灵敏度、失真、信噪比、延迟等等。

（2）分割器

例如：传感器的感兴趣基元文本切割、脑电波的时长等等。关注部分与整体关系。

（3）特征提取器

类内一致性：来自同一类别的不同样本特征值相近。

类间差异性：来自不同类别的样本特征值有很大差异，如表征能力、鉴别性、特征维度。

例如：基于深度神经网络的特征表征学习。

（4）分类器

根据特征提取器提取的特征向量给被测试对象(样本)赋予类别标记。

例如：贝叶斯决策(最小欧式/马氏距离分类器)、HMM。例如：SVM、感知器模型、Logistic 回归。

（5）后处理器

根据上下文信息对分类进行调整。

---

模式识别系统实例：人脸认证/识别

1. 数据准备：利用摄像头采集图像；从网络等开放媒体搜集数据；人工标注数据；划分训练集、验证集和测试集。
2. 特征提取：基于深度网络的特征表征学习，包括深度神经网络设计、损失函数设计等。
3. 分类器选取与训练：可以选择基于深度网络的分类决策、Bayes 决策、Logistic 回归、Fisher 线性判别、SVM 等。
4. 分类决策：可以选择基于深度网络的分类决策。
5. 系统部署。

8.5.2 系统性能评价

错误率(error rate) 与 准确率(accuracy):

错误率 为 分类错误的样本占样本总数的比例。假设 $N$ 个样本中有 $a$ 个样本分类错误，则 $E=a/N$ 。准确率 为 1减去错误率，即为： $1-a/N$ 。

误差(error):

学习器的实际预测输出 与 样本的真实输出之间的差异。分为：训练误差/经验误差(empirical error)、测试误差/泛化误差(generalization error)。

分类结果的混淆矩阵：

真实类别 $\bigg\backslash$ 预测类别	正例	反例
正例	TP (真正例)	FN (假反例)
反例	FP (假正例)	TN (真反例)

召回率 Recall、精确率 Precision：

$$\text{Recall} = \frac{TP}{TP + FN}, \quad \text{Precision} = \frac{TP}{TP + FP}$$

召回率是“实际为正例的样本中，有多少被预测为正例”，精确率是“预测为正例的样本中，实际有多少是真的正例”。

希望召回率高相当于是“宁可错杀，不可放过”，希望精确率高相当于是“宁可漏判，不可错杀”。召回率衡量了发出去的样本中有多少被“召回”了，精度则描述了预测时有多“精准”。

recision 和 recall 是不可兼得的。想要 recall 高，就要多预测，没那么自信的也预测为正样本，才能尽可能覆盖更多的原始正样本；而想要 precision 高，就要少预测，有十足把握才预测正样本，这样才能更精确。对于火灾这类问题而言，预测错的代价不高，而漏预测的代价很高，因此需要强调 recall，方法是降低预测正样本的阈值，使模型更倾向于预测正样本。

真阳性率 TPR (True Positive Rate)、假阳性率 FPR (False Positive Rate)：

$$\text{TPR} = \frac{TP}{TP + FN}, \quad \text{FPR} = \frac{FP}{TN + FP}$$

ROC 曲线：

ROC (Receiver Operator Characteristic) 曲线，称为受试者工作特征曲线或接收者操作特性曲线，是以假阳性率 FPR 为横坐标，以真阳性率 TPR 为纵坐标，绘制的曲线。

AUC 曲线 (Area Under Curve) 是 ROC 曲线下的面积，表示分类器的性能。AUC 的值范围在 0 到 1 之间，值越大表示分类器性能越好。AUC 用于衡量模型对正类和负类的区分能力，即：从所有正类和负类中随机选一个，模型将正类排在前面的概率。特点：与具体阈值无关；适合二分类问题。

思考一下什么样的 ROC 曲线代表高性能的模式识别系统？答：ROC 曲线越接近 左上角 越好，因为 FPR 越小越好， TPR 越大越好。

PR 曲线：

PR (Precision-Recall) 曲线，是以召回率 recall 为横坐标，精度 precision 为纵坐标，绘制的曲线。

AP 曲线 (Average Precision) 是 PR 曲线下的面积。AP 用于衡量模型在不同 recall 水平下的平均准确率，即：所有召回水平下，精度的加权平均（更关注排序前段的准确性）。多用于目标检测（如 COCO）或信息检索，常和 mAP (mean AP) 配合使用（多个类别取平均）。

单词测试使用固定的阈值，计算出 recall 和 precision。多次测试使用不同的阈值，得到多组 precision 和 recall 值，就能绘制出 PR 曲线。

F-score：

F1-score 是精度和召回率的调和平均数，综合考虑了精度和召回率的平衡。公式为：

$$F_1 = 2 \cdot \frac{PR}{P+R} = 2 \cdot \frac{TP}{2TP + FP + FN} \\ F_\beta = (1+\beta^2) \cdot \frac{PR}{(\beta^2) P + R}$$

F-score 最理想的数值是趋近于1，此时 precision 和 recall 都很高，接近于1。

交叉验证 Cross Validation：

1. 交叉验证是用来验证分类器的性能一种统计分析方法，将原始数据(dataset)进行分组，一部分做为训练集(training set)，另一部分做为验证集(validation set)。
2. K-折交叉验证(K-fold Cross Validation)：将原始数据分成 $K$ 组(一般是均分)，将每个子集数据分别做一次验证集，其余的 $K-1$ 组子集数据作为训练集，这样得到 $K$ 个模型。把这 $K$ 个模型在最终验证集的分类准确率的平均数，作为分类器的性能指标。
3. 留一法(Leave-One-Out)：每个样本单独作为验证集,其余的 $N-1$ 个样本作为训练集。

过拟合/欠拟合、生成式模型/鉴别式模型，前面已经讨论过，可见 第3讲 - Machine Learning。

Comments