6 图像复原¶
6.1 图像退化和复原模型¶
图像退化:实际应用中,无论是由光学,光电方法,还是电子方法获得的图像,都会有不同程度的退化。
退化原因:传感器内部噪声,摄像机未聚焦,物体与镜头之间相对移动,胶片的非线性和几何畸变,光学成像系统中孔径衍射。
退化实例:运动模糊,几何畸变,大气湍流影响。
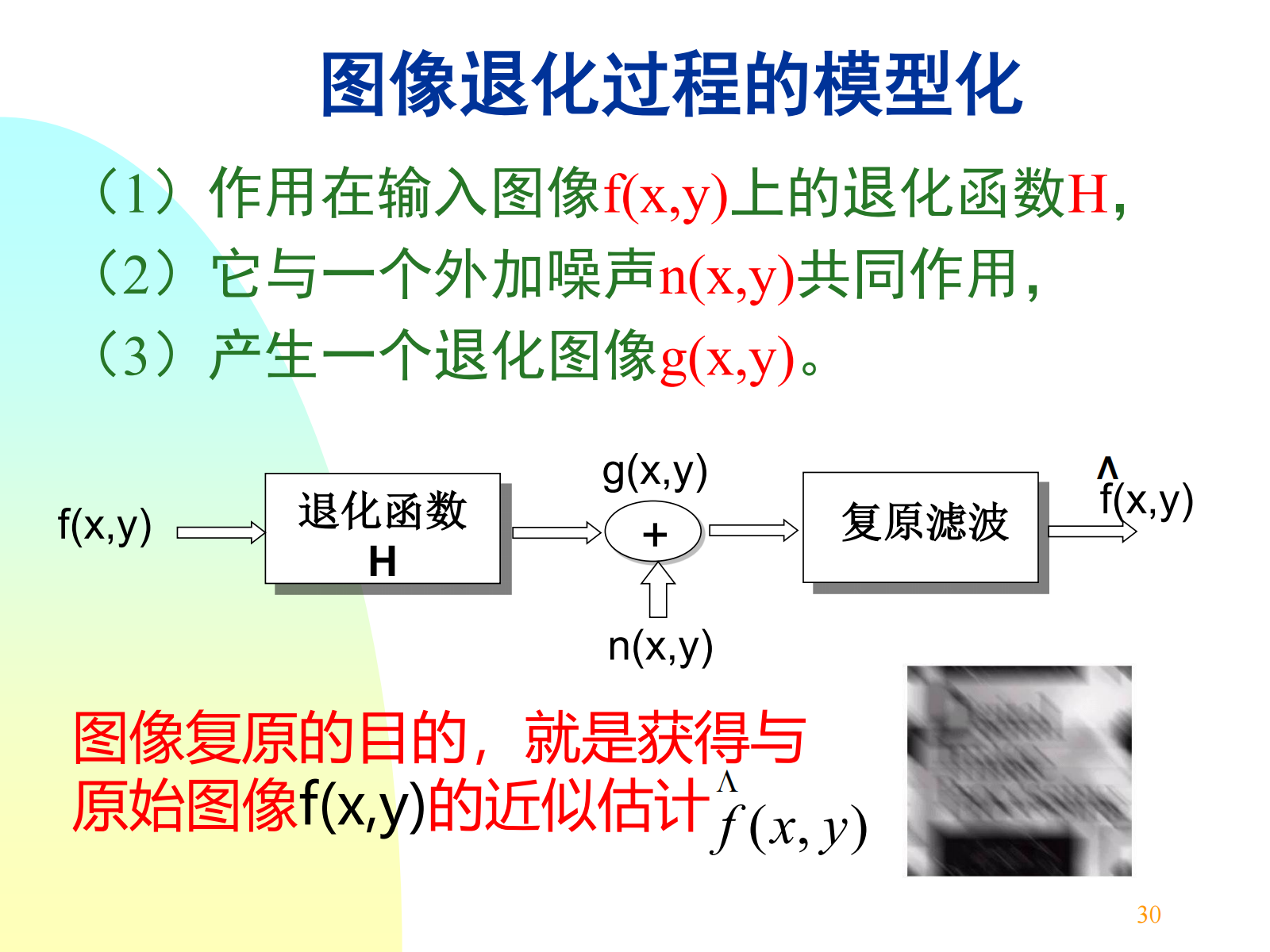
图像复原:利用退化现象的某种先验知识,复原被退化的模糊图像。复原技术就是把退化过程模型化,采用相反的过程处理,复原原图像。
图像复原和图像增强的联系,见图片:
退化过程原理:(退化可以理解为使图像变形、失真等等操作,不同于加噪声。)
非线性系统模型更具有普遍性,但它却常无解或难于计算。因此图像复原中,往往用线性系统近似,模拟非线性系统模型。
图像超分辨率(Image Super Resolution):由一幅低分辨率图像或图像序列恢复出高分辨率图像。方法:基于插值,基于重建,基于学习。
补充常见插值方法:
- 最近邻插值:选取离待插值点最近的点的像素值作为待插值点的像素值;会出现锯齿效应。
- 双线性插值:在x和y两个方向上分别进行线性插值;不会出现锯齿效应,但比较模糊。
- 双三次插值:通过最近的16个采样点的加权平均得到,需要使用两个多项式插值三次函数,每个方向使用一个。计算量比较大,但效果相对较好。
低分辨率人脸图像重建与识别系统。人脸超分辨率:针对低分辨率条件例如监控场景,利用局部纹理或者结构信息进行人脸超分,并服务于后续的人脸识别等任务。研究难点为:如何在超分过程中保持身份信息,避免得到“平均脸”;如何充分利用人脸结构特征,有针对性的重建人脸。
图像超分辨率重建:给定的低分辨率图像通过特定的算法恢复成相应的高分辨率图像,是一种欠定问题,旨在克服或补偿由于图像采集系统或采集环境本身的限制,导致的成像图像模糊、质量低下、感兴趣区域不显著等问题。
传统图像超分辨率通过插值来实现,例如最近邻插值、双线性插值、双三次插值等,通过邻域的像素信息拟合未知的像素,这种方式假设像素变化是连续、平滑的,因此在处理边缘、纹理处时效果差。
通用超分辨率:根据低分辨率图像重建得到对应的高分辨率图像;利用局部纹理或者内容信息恢复图像细节;经典深度学习方法有 SRCNN, EDSR, SRGAN 等。
图像退化模型的数学表达¶
线性系统就是具有均匀性和相加性的系统。
若不考虑噪声, \(n(x,y)=0\) ,退化系统模型 \(H\) 具有性质:相加性、一致性、线性、位置/空间不变性(线性系统在图像任意空间位置的响应只与在该空间位置的输入值有关,而与空间位置本身无关)。
一维退化模型的离散计算(不考虑噪声):
注意 \(f(x),g(x)\) 都要补0,扩展为 \(f_e(x),g_e(x)\) .
推广到二维L:
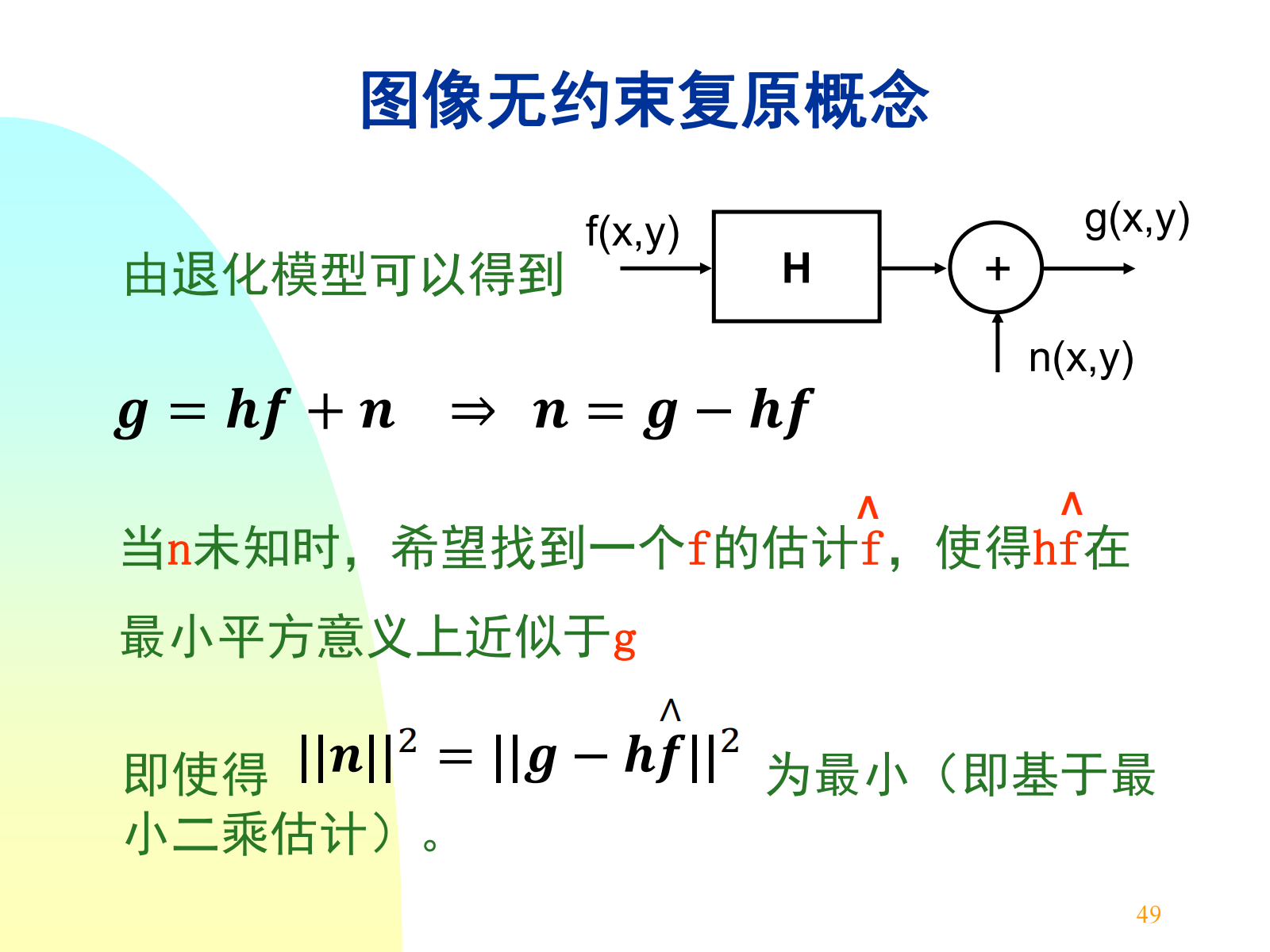
6.2 图像无约束复原¶
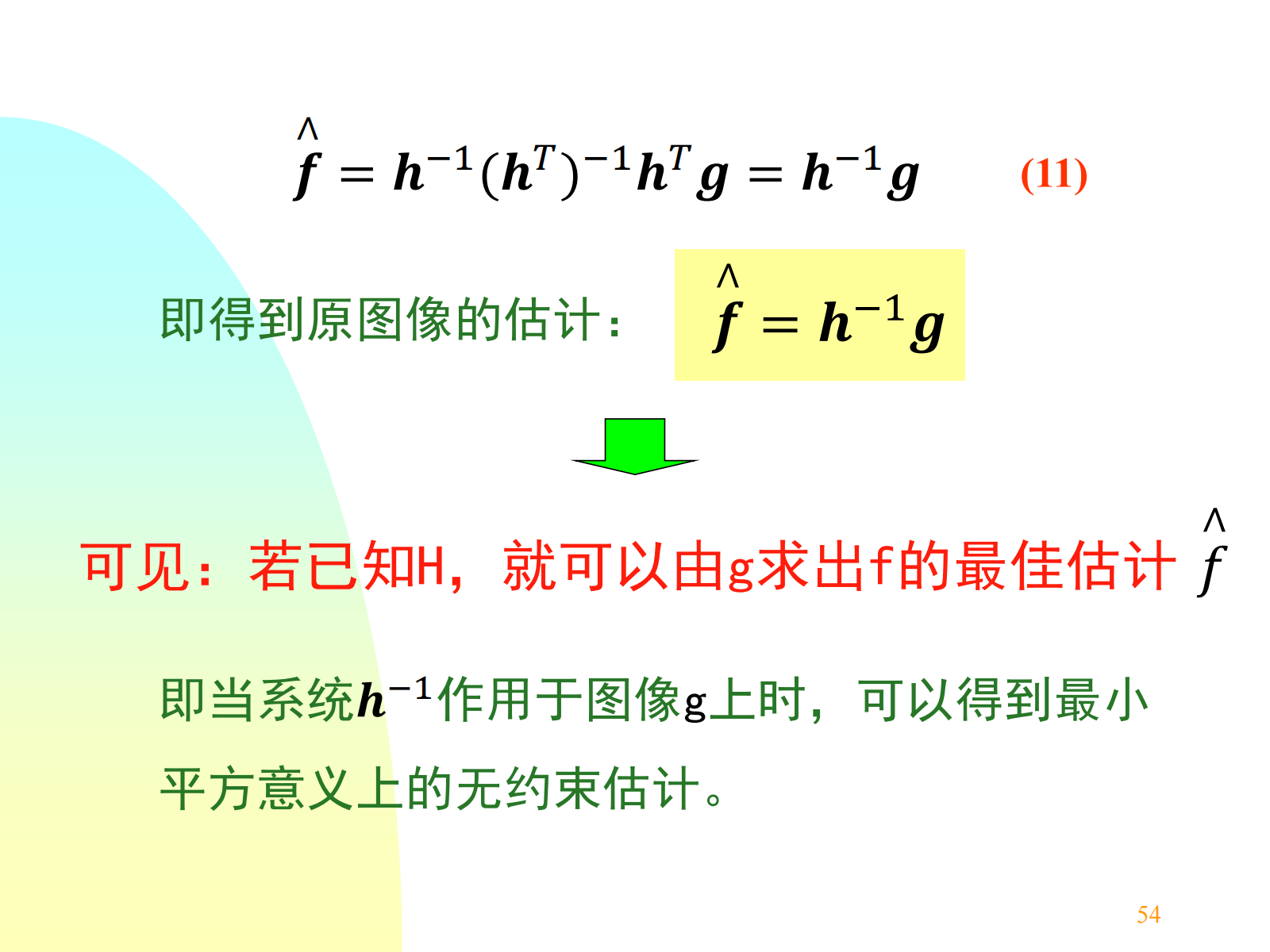
逆滤波(频域复原方法):不考虑噪声时,已知退化图像的傅里叶变换 \(G(u,v)\) 和“滤波”传递函数 \(H(u,v)\) ,可得原图像傅里叶变换 \(\hat{F}(u,v)\) ,再求反变换,即可得原图像的估计 \(\hat{f}(x,y)\) .
因此,实际的原始图像傅里叶估计为 \(\hat{F}(u, v) = [F(u, v)H(u, v) + N(u, v)] \cdot M(u, v)\) .
逆滤波实例:大气湍流模型退化函数 \(H(u, v) = \mathrm{e}^{-k[(u-M/2)^2 + (v-N/2)^2]^{5/6}}\) .
估计 \(H(u,v)\) :
实验估计:使用相同系统对一个冲激(小亮点),得到退化的冲激响应。由于冲激的傅里叶变换是常量,可得 \(H(u,v)=G(u,v)/A\) ,A是一个描述冲激强度的常量。也就是让冲激通过系统得到冲激的退化。
建模估计,例如二维方向运动模糊,设 \(T\) 为曝光时间(运动模糊的时间), \(c\) 和 \(b\) 分别为 x 方向和 y 方向的位移。退化函数为:
问题:当 \(u=n/c\) 时 \(H(u,v)=0\) ,在这些点上无法用逆滤波方法复原出原图像。因此不能取 u 在这些点的值,需采用其他方法解决。
运动模糊是指在拍摄过程中,由于相机或拍摄对象的移动导致图像模糊的现象。运动模糊的本质是不同位置光强的积分,在相机抖动、长曝光、高速运动等场景下会导致严重的图像质量下降。真实世界中的运动模糊是非常复杂的。
失焦模糊(Defocus Blur)是指当被拍摄物体不在镜头的焦平面上时,由于镜头景深限制而产生的模糊现象。失焦模糊的产生主要是由于镜头的景深限制。
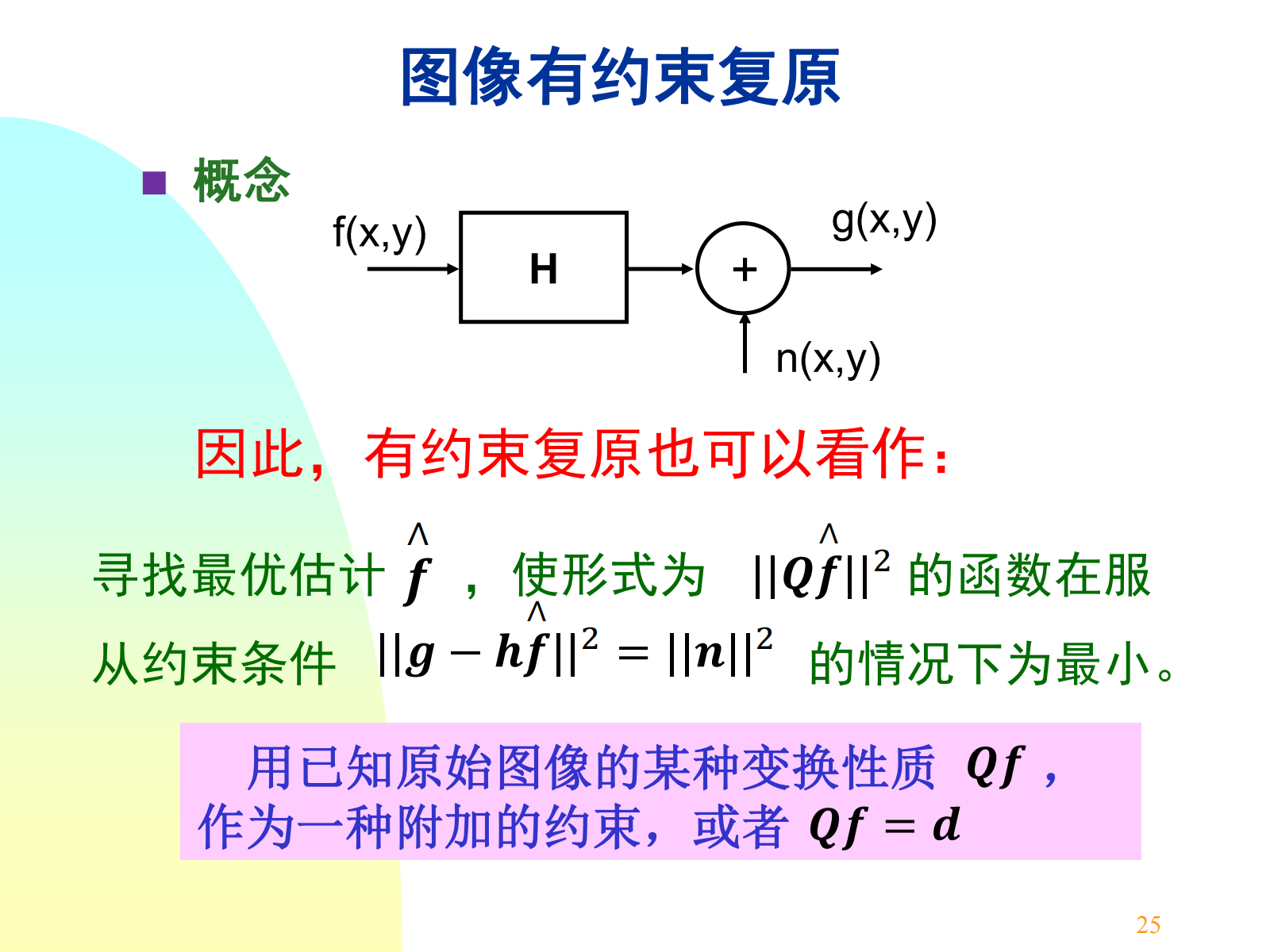
6.3 图像有约束复原¶
在无约束图像复原中,只要已知退化函数 \(H(u,v)\) 即可进行图像复原。但是实际图像存在噪声!
有约束复原,是指除了已知退化系统传递函数外,还要根据其他条件作为约束:噪声统计特性和噪声与图像的相关信息。
有约束复原,即是求有附加条件的极值问题,仍然采用拉格朗日乘数法解决。
维纳滤波¶
也称最小均方误差滤波。维纳滤波综合考虑退化函数和噪声统计特性两个方面。前提:假定噪声和图像不相关。
复原图像的傅里叶变换的估计为:
通常, \(s=1\) 称为维纳滤波器, \(s\ne 1\) 时称为参数维纳滤波器,也称为最小均方误差滤波器。
实际中 \(S_n(u,v),S_f(u,v)\) 很难已知,常做近似 \(s=1\) ,将噪声用白噪声近似, \(S_n(u,v)/S_f(u,v)\) 代表“噪声与信号的功率密度比”为常数 \(K\) .
Quote
有噪声时维纳滤波效果比逆滤波强。噪声较大时逆滤波的处理结果几乎完全失真。
维纳滤波,假定原始图像 f 和噪声 n 是随机变量,其图像集形成平稳随机过程,并需要已知未退化图像和噪声的功率谱。虽然可以近似,但常数 K 不易估计。即:维纳滤波器在图像统计最小二乘误差意义下最优,但对某一具体图像而言不一定最优。
最小平方法¶
有约束最小平方复原,只要求噪声方差和均值信息就可对给定图像复原出最优结果。
最小平方复原的目标是寻找一种准则函数,由此导出的复原对每一幅具体图像确定一个最优的评判标准。在逆滤波中,由于 \(H(u,v)\) 的病态性质,导致在其零点附近数值变化起伏过大,产生多余噪声和虚假边缘,会造成图像严重失真。而图像的灰度变化是平滑的、少跳变。因此,可采用最大平滑测度准则。
图像相邻像素间平滑性可通过二阶导数表征:二阶导数小,灰度跳变小,图像平滑,所以可作为图像复原时的约束条件 \(Qf\) .
二阶导数的差分形式:
也可写成图像 \(f(x,y)\) 与模板 \(p(x,y)\) 卷积的结果:
最终推导得到:
其中 \(P(u,v)\) 为模板卷积核 \(p(x,y)\) 的傅里叶变换。s 参数需要被调整以满足式 \(\|n\|^2 =\|g - \hat{hf}\|^2\) . 对于一幅 N×N 大小的图像,噪声功率为 \(\|n\|^2 = N^2\sigma^2 + m^2\) ,其中 \(m\) 和 \(\sigma\) 分别为噪声的均值和方差。
两种有约束复原方法总结
评价标准:维纳滤波在图像复原误差统计平均意义下最优;最小平方在最大平滑准则下最优。
应用场景:维纳滤波中,图像和噪声都属于随机过程,且已知噪声和未退化图像功率谱,或用常数替代(该值不易找到)。最小平方中以像素间平滑准则为基础,只需要知道噪声的均值和方差或者迭代选择标量参数 s。