Skip to content

OJ6：跳跳乐⚓

Description⚓

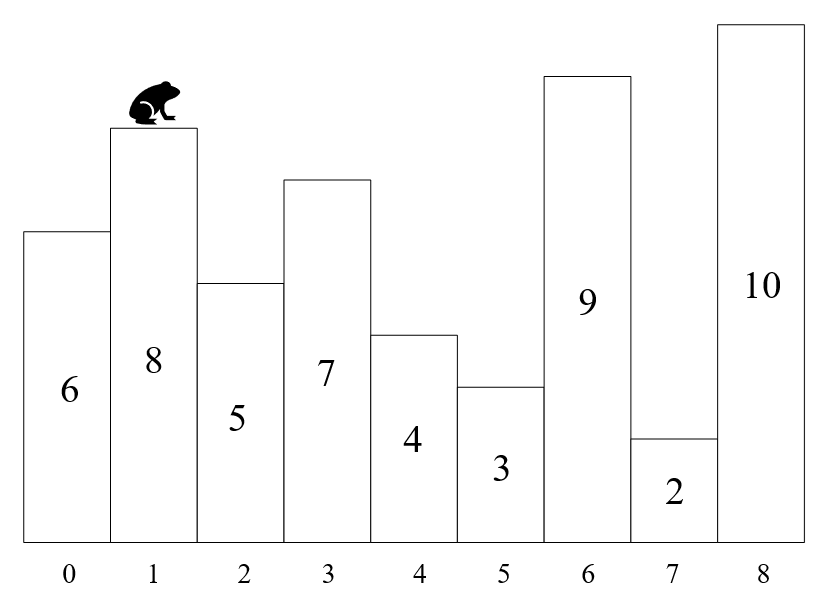
有一系列相邻的台阶，每级台阶具有不同的高度，台阶间的水平距离相等，如图所示

oj6_description

有一只青蛙在不同台阶之间跳跃，设青蛙可以跳跃的最长水平距离为 K 个台阶，最大的垂直距离为 H（需要注意的是，为简化问题，垂直距离只需考虑跳跃起点和终点的高度差，不需要考虑途中经过的台阶高度和起点的高度差），以上图为例，若 K=5,H=2，则青蛙可以从当前位置跳跃到编号为 {0, 3, 6} 的三个台阶，因为这三个台阶与当前台阶的水平距离均不大于5，且垂直距离的绝对值分别为 {2, 1, 1} ，均不大于2。

现在总共有 M 个连续台阶，并给定每个台阶的高度，试求青蛙一共可能在多少对台阶间跳跃？

Input⚓

输入为两行

第一行为三个整数，分别为台阶数量 M，青蛙可以跳跃的最长水平距离 K，可以跳跃的最大垂直距离 H。

第二行为 M 个整数，依次为各个台阶的高度。

Output⚓

输出为一个整数，为青蛙可以跳跃的台阶对数。

Example⚓

Text Only
input:
9 5 2
6 8 5 7 4 3 9 2 10

output:
14

解释：可跳跃的台阶对编号分别为(0, 1), (0, 2), (0, 3), (0, 4), (1, 3), (1, 6), (2, 3), (2, 4), (2, 5), (3, 6), (4, 5), (4, 7), (5, 7), (6, 8)

Hint⚓

输入数据范围：

\(M<2^{31},K<2^{31},H<2^{31}\)，每级台阶的高度也小于 \(2^{31}\) 。

相邻两个台阶间的水平距离均相等且值为1，任意两个台阶的高度均不相等。

Solution⚓

（1）维护一个长度为一个 \(K\) 的有序数组（从小到大）std::vector<int> stair 。

刚开始 stair 为空，逐渐读入元素 height 直到数组容量达到 \(K\)，找到它能够跳到的元素个数，通过二分插入的方法，调用 insert() 函数，将 height 插入数组中，此时数组仍保持有序。

当数组容量达到 \(K\) 后，每次读入一个元素 height 时，数组中所有元素恰好是它前面 \(K\) 个元素，首先找到它能够跳到的元素个数，然后删除距离它为 \(K\) 那个元素，再通过二分插入的方法，调用 insert() 函数，将 height 插入数组中，此时数组大小仍为 \(K\) 且保持有序。

至于这一步要删除哪个元素，使用另外一个大小为 \(M-K\) 的数组 std::vector<int> dele 存放，然后在这一步调用 std::vector 的 erease(),remove() 函数删除特定值的元素。

（2） \(K\geqslant M-1\) ，第一个台阶和最后一个台阶的水平距离差为 \(M-1\)，不超过 \(K\)，因此所有台阶都不再受水平距离的限制。在上述步骤中无需再使用额外的数组 std::vector<int> dele 存放要删除的元素。

（3）计算 height 能够跳到的元素个数的方法是：由于数组 stair 是从小到大有序的，在数组中从小到大找到第一个大于 height - H 的元素索引 min（下界），从大到小找到第一个小于 height + H 的元素索引 max （上界），则 height 能跳到的元素个数为max - min + 1 。

Code⚓

C++
#include <cstdio>
#include <vector>
#include <algorithm>

long long search(std::vector<int> &vec, int height, int H)
{
    long long min = 0, max = vec.size() - 1;
    long long i = 0;
    for (i = 0; i < vec.size(); i++)
    {
        if (vec[i] >= height - H)
        {
            break;
        }
    }
    min = i;
    for (i = vec.size() - 1; i >= 0; i--)
    {
        if (vec[i] - H <= height)
        {
            break;
        }
    }
    max = i;
    return max - min + 1;
}

int main(int argc, const char* argv[])
{
    int M, K, H;
    long long count = 0;
    scanf("%d%d%d", &M, &K, &H);
    if (K < M - 1)
    {
        std::vector<int> stair;
        int height = 0;
        std::vector<int> dele(M - K, 0);
        for (int i = 0; i < M; i++)
        {
            scanf("%d", &height);
            count += search(stair, height, H);
            if (i < M - K)
            {
                dele[i] = height;
            }
            if (i >= K)
            {
                // 先删除一个元素
                stair.erase(remove(stair.begin(), stair.end(), dele[i - K]), stair.end());
            }
            // 二分插入新的元素
            int left = 0, right = stair.size() - 1;
            int mid;
            while (left <= right)
            {
                mid = left + (right - left) / 2;
                if (height < stair[mid])
                {
                    right = mid - 1;
                }
                else
                {
                    left = mid + 1;
                }
            }
            stair.insert(stair.begin() + left, height);
        }
    }
    else
    {
        // K>=M-1，全区间都可能跳跃
        std::vector<int> stair;
        int height = 0;
        for (int i = 0; i < M; i++)
        {
            scanf("%d", &height);
            count += search(stair, height, H);
            //  二分插入新的元素
            int left = 0, right = stair.size() - 1;
            int mid;
            while (left <= right)
            {
                mid = left + (right - left) / 2;
                if (height < stair[mid])
                {
                    right = mid - 1;
                }
                else
                {
                    left = mid + 1;
                }
            }
            stair.insert(stair.begin() + left, height);
        }
    }
    printf("%lld", count);
    return 0;
}

Comments