第五章固体间接触的电特性⚓

说明

本章理论公式较少，模型和图形较多，建议结合教材图片学习。

5.1 功函数与接触电势⚓

Note

经典电子论按照经典的玻尔兹曼统计分布，量子理论考虑泡利不相容原理，按照费米-狄拉克统计分布。

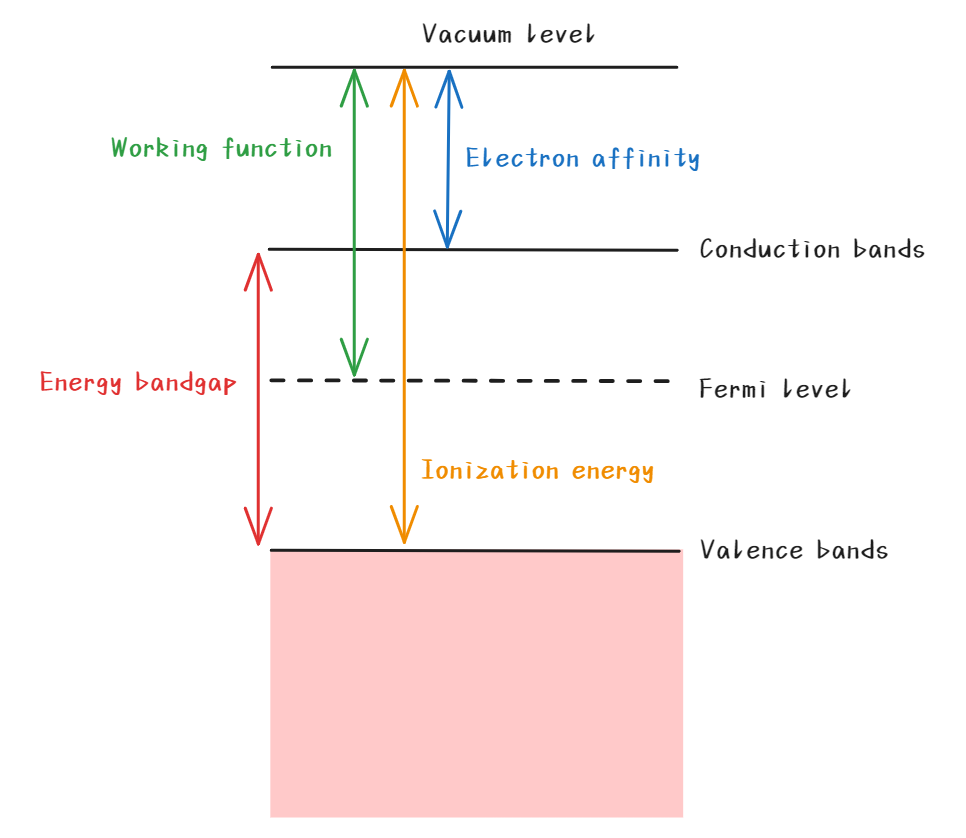
经典电子论中，电子的功函数为电子真空能级与导带底能量之差。

电子亲和能 \(\chi\) 代表无穷远处电子真空能级到导带底（势阱底部）的能量差，由材料本身性质决定。

电离能代表从真空能级到价带顶的能量差。

量子理论中，功函数表示真空能级与费米能级之差： \(W=\chi-E_F\) 。即：一个起始能量等于费米能级的电子，由金属内部逸出到真空中所需要的最小能量。一般选定真空能级为零点，这样功函数可以反映费米能级的高低。

经过推导可知，金属热电子发射的发射电流与温度呈指数关系，电子是从费米面发射的。

接触电势：不同导体 A 和 B，接触或导线连接，会带电并产生不同的电势 \(V_A,V_B\) 。

不同金属的功函数不同，即费米能级不同，接触后，电子发生流动，形成接触电势差，接触电势差阻止电子继续流动，此时金属的费米能级达到平衡。

A,B 金属接触后：

电子从费米能级高的金属 A 流向费米能级低的金属 B。
电子运动使费米能级高的 A 带正电荷，费米能级低的 B 带负电荷，产生静电势 \(V_A>0, V_B<0\) ，电子产生不同的附加静电势能。A,B 的能级同时发生变化，费米能级相互靠近。
平衡状态下，费米能级相等，电子不再流动。
形成的接触电势差 \(V_A-V_B=(W_B-W_A)/e\) 。因为此时费米能级相等，所以相当于接触电势差就是两个金属的功函数之差除以元电荷。

两个导体依靠产生接触电势差，补偿它们原本费米能级的差别，从而使电子达到统计平衡。

5.2 PN 结⚓

结的概念：半导体与不同材料之间构成的界面

不同掺杂类型的材料：同质 PN 结。
不同半导体：半导体异质结（pN 结，Pn 结）。
半导体与金属：肖特基结。
半导体与绝缘体-金属：MOS 结（MIS 结）。

结的用途：

微电子：各种二极管、晶体管。
光电子：发光二极管、激光器、探测器。

注：掺杂类型相同但浓度不同也能形成结，会导致能带弯曲。

5.2.1 PN 结的形成⚓

PN 结的性质集中反映了半导体导电性能的特点：存在两种载流子，载流子有迁移、扩散和产生-复合三种基本运动形式。在不同情况下，这三种运动形式对导电性能的贡献各不相同。

在一块本征半导体上，用不同的掺杂工艺，使一边形成 N 型半导体，另一边形成 P 型半导体。N 型半导体的费米能级接近导带，P 型半导体的费米能级接近价带，因此 N 区费米能级更高 \(E_{FN}>E_{FP}\) ，费米能级之间存在能级差，存在载流子浓度差。

PN 结的形成：

电子从费米能级较高的 N 区流向 P 区（扩散运动），N 区缺少了电子，原本电中性的 N 区在界面附近出现正电荷积累（带正电的施主离子）。
从 N 区扩散来的电子与 P 区的多子空穴复合，使得原本电中性的 P 区在界面附近耗尽了空穴，产生负电荷积累（带负电的受主离子）。
杂质离子的正负电荷在界面附近形成由 N 区指向 P 区的内建电场（自建场）。在自建场作用下，P 区的少子电子向 N 区漂移，N 区的少子空穴向 P 区漂移。
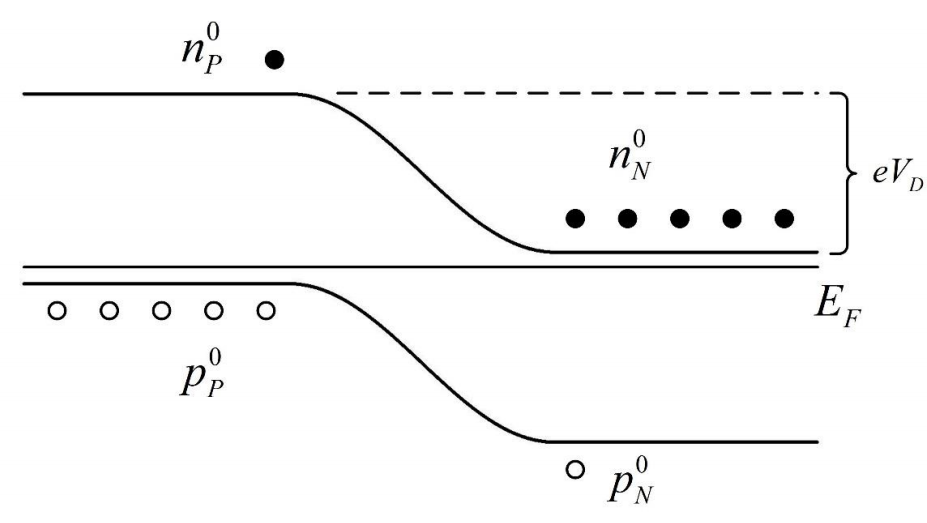
稳态时，载流子扩散和漂移运动动态平衡，P 区和 N 区的费米能级拉平。
效果上来看，费米能级较高的 P 区整体能级下降，费米能级较低的 N 区整体能级上升。此时 N 区的导带底比 P 区的导带底更高，能级高了 \(eV_D=E_{FN}-E_{FP}>0\) 。

即：载流子浓度差 → 多子扩散-复合 → N 区失去电子留下带正电的施主离子，P 区失去空穴留下带负电的受主离子 → 形成空间电荷区 → 形成内建电场 → 少子漂移运动 → 扩散与漂移动态平衡 → 空间电荷区稳定 → 形成平衡 PN 结

P 区与 N 区接触界面形成一个能带过渡区，称为 空间电荷区(space charge region)/耗尽区，性质：

宽度约为微米 \(\mu \text{m}\) 数量级，不存在可移动的电子和空穴。
内建电场由固定电荷（不可移动的正负离子）产生，这些固定电荷是 “N 区电子减少留下带正电的施主离子”和 “P 区空穴减少留下带负电的受主离子”。一般均匀掺杂情况下，杂质离子均匀分布，净电荷为0。
内建电场方向从 N 区指向 P 区，形成对多子（N 区电子和 P 区空穴）的势垒，高度为 \(eV_D=E_{FN}-E_{FP}>0\) ，称为平衡 PN 结势垒，阻碍多子进一步扩散。
平衡 PN 结势垒高度为接触前费米能级之差，也为平衡后导带底、价带顶的能级差： \(eV_D=E_{FN}-E_{FP}=E_{CP}-E_{CN}=E_{VP}-E_{VN}\) 。
内建电场的电场强度大致为：左边界 \(-x_p\) 处场强为0，向右开始线性增加，在 \(x=0\) 处场强最大（负数），再向右线性减小，右边界处 \(+x_n\) 减小为0，电场始终为负数。左右分布不一定对称，因为 \(x_p= x_n\) 不一定成立。
空间电荷区宽度与掺杂浓度呈反比 \(N_a x_p=N_d x_n\) ，\(N_d,N_a\) 分别为施主杂质浓度、受主杂质浓度。且主要在低掺杂区域。

事实上，通过严格计算可以得到空间电荷区的左右宽度和电场强度最大值：

\[ x_n=\sqrt{\frac{2\varepsilon_s V_d}{q} \cdot \frac{N_a}{N_d(N_a+N_d)}} \\ x_p=\sqrt{\frac{2\varepsilon_s V_d}{q} \cdot \frac{N_d}{N_a(N_a+N_d)}} \\ E_{\max}=-\frac{qN_d x_n}{\varepsilon_s} \]

空间电荷区是载流子的耗尽区，因此载流子浓度接近本征载流子浓度，费米能级接近于本征费米能级。因此在界面处，费米能级靠近禁带中央。向 P 区，价带顶向上弯曲靠近费米能级；向 N 区，导带底向下弯曲靠近费米能级。

PN 结能带大致画法：

确定 PN 结势垒 \(eV_D=E_{FN}-E_{FP}\) 。
由掺杂浓度大小关系，确定空间电荷区左右宽度比例（反比关系）。
分别用抛物线型画出空间电荷区的能带曲线，因为电场强度是线性变化的。

平衡状态下的结区两边的载流子浓度（上标为0代表平衡时）

P 区和 N 区的电子浓度之比：

\[ \frac{n_P^0}{n_N^0} = \frac{\mathrm{e}^{-(E_{CP} - E_F)/k_B T}}{\mathrm{e}^{-(E_{CN} - E_F)/k_B T}} = \exp(-eV_D / k_B T) \]

N 区和 P 区的空穴浓度之比：

\[ \frac{p_N^0}{p_P^0} = \frac{\mathrm{e}^{-(E_F - E_{VN})/k_B T}}{\mathrm{e}^{-(E_F - E_{VP})/k_B T}} = \exp(-eV_D / k_B T) \]

由于 \(eV_D=E_{FN}-E_{FP}\) ，可见平衡状态下载流子浓度之比由接触前的费米能级差决定。

5.2.2 PN 结的单向导电性⚓

若在 PN 结上加一外电压 \(V\)，由于空间电荷区中载流子浓度很低，电阻很高，因此外加电压基本都加在空间电荷区。PN 结势垒将改变 \(eV\) ，从而破坏了原来载流子扩散和迁移的平衡，引起载流子重新分布。

P 区接正极、N 区接负极，称为正向偏压，反之称为反向偏压。

注意，这里的单向导电特性，主要是研究 PN 结也就是空间电荷区的载流子。加入正向/反向偏压，绘制能带图的时候需要考虑准费米能级，N 区和 P 区的准费米能级不相等。

PN 结正向注入⚓

当 PN 结加正向偏压 \(V\) （P 指向 N）时，外加电压使内建电场减弱，空间电荷区变窄，PN 结势垒降低为 \(e(V_D-V)\) ，打破了迁移运动与扩散运动的相对平衡。漂移运动减弱，电子源源不断地从 N 区扩散到 P 区，空穴源源不断地从 P 区扩散到 N 区。它们属于非平衡载流子。

势垒边界上的少数载流子，P 区电子和 N 区空穴，其浓度（由于非平衡，所以无上标0）近似根据 Boltzmann 统计求得：

\[ n_P=n_P^0 \mathrm{e}^{eV/k_B T} \\ p_N=p_N^0 \mathrm{e}^{eV/k_B T} \]

外加电压使边界处电子积累，浓度大大提高，产生的非平衡载流子浓度为：

\[ \Delta n_P=n_P-n_P^0=n_P^0(\mathrm{e}^{eV/k_B T}-1) \\ \Delta p_N=p_N-p_N^0=p_N^0(\mathrm{e}^{eV/k_B T}-1) \]

其中共有的一项 \((\mathrm{e}^{eV/k_B T}-1)\) 代表非平衡载流子浓度增加的倍数。

这些边界处的非平衡载流子（少子）边扩散边复合，向体内运动（注意，不是向空间电荷区），形成扩散电流（扩散是因为存在浓度差，复合是因为遇到了多子）。注入到 P 区的电子的扩散电流密度和注入到 N 区的空穴的扩散电流密度分别为：

\[ j_{n}=e \frac{D_n}{L_n} n_P^0 \left(\mathrm{e}^{eV/k_B T}-1\right) \\ j_{p}=e \frac{D_p}{L_p} p_N^0 \left(\mathrm{e}^{eV/k_B T}-1\right) \]

通过单位面积 PN 结的总电流，为二者相加，因为电子与空穴运动方向相反，电流方向相同：

\[ j=j_{n}+j_{p}=e \left(\frac{D_n}{L_n} n_P^0 + \frac{D_p}{L_p} p_N^0\right) \left(\mathrm{e}^{eV/k_B T}-1\right) =j_s \left(\mathrm{e}^{eV/k_B T}-1\right) \]

这表明，在正向偏压下，通过 PN 结的电流与少子的浓度成正比，且随正向偏压的增大按照指数规律迅速增大。这就是二极管中正向导通的由来。

\(D_n,L_n,D_p,L_p\) 的关系

\(D_n=\dfrac{L_n^2}{\tau_{n0}}, D_p=\dfrac{L_p^2}{\tau_{p0}}\) ，式中 \(\tau\) 为弛豫时间。

PN 结反向抽取⚓

当 PN 结外加反向偏压 \(V\) （N 指向 P）时，外加电场使内建电场增强，空间电荷区变宽，使 PN 结势垒增大为 \(e(V_D+V)\) 。此时载流子的漂移运动超过了扩散运动。在反向偏压的作用下，N 区中的空穴一旦到达空间电荷区的边界，就会被电场拉向 P 区；P 区中的电子一旦到达空间电荷区的边界，就会被电场拉向 N 区。这就是 PN 结的反向抽取作用，对应二极管的反向截止。

边界处的少子浓度：P 区边界电子浓度和 N 区边界空穴浓度下降到趋于0：

\[ n_P=n_P^0 \mathrm{e}^{-eV/k_B T} \to 0 \\ p_N=p_N^0 \mathrm{e}^{-eV/k_B T} \to 0 \]

反向抽取使 PN 结界面处的载流子浓度小于其平衡浓度，此时非平衡载流子浓度为负值，这意味着载流子的复合率为负值，即在外电场的作用下，实际上有新的电子-空穴对产生，其中的少数载流子可能扩散到空间电荷区，而被电场拉向对面，形成反向电流。所以，PN 结的反向电流实质上就是产生电流。

反向电流是由在 PN 结附近所产生、又有机会扩散到空间电荷区边界的少数载流子形成。通常由于少数载流子的浓度很低，因此在一定的反向电压范围内，反向电流一般都很小。

\[ j\approx j_s = -e \left(\frac{D_n}{L_n} n_P^0 + \frac{D_p}{L_p} p_N^0\right) \]

但是，如果有外界作用，使得达到反向 PN 结空间电荷区边界的少数载流子浓度很高，这些载流子同样可以被空间电荷区的电场拉向对面，形成大的反向电流。如 NPN 晶体管正向发射结把电子注入到 P 型区，由于基区的宽度远远小于扩散长度，注入到基区的电子来不及复合，就扩散到反向集电结的边界，被反向集电结的抽取作用拉向集电区，形成集电结反向大电流状态，这就是晶体管电流放大作用的物理基础。

PN 结的反向击穿（反向电压超过一定门限后，反向电流会迅速增加，对应电压为击穿电压）：

齐纳击穿：重掺杂的 PN 结发生隧穿，价带电子跃迁到导带。
雪崩击穿：空间电荷区电子能量过大，与耗尽区原子碰撞产生新的电子空穴对。
热电击穿：结区热积累。

双极型晶体管(BJT, bipolar junction transistor)：由两个 PN 结构成的具有放大作用的半导体器件，参与导电的有电子和空穴两种载流子。有 NPN 和 PNP 两种结构。

光电二极管

光电二极管通常工作于反向偏置：增加空间电荷区宽度，提高对光生载流子的收集效率，且有利于光生电子-空穴对漂移分离，形成光电流。因此应正极接 N 区，负极接 P 区。

总结⚓

平衡态：耗尽层中能带弯曲形成势垒，扩散与漂移动态平衡。

正偏：扩散势垒变低，耗尽层变窄，扩散>漂移，产生正向电流。

反偏：扩散势垒变高，耗尽层变宽，扩散<漂移，产生反向电流（击穿）。

\(j_s\) 为理想反向饱和电流，主要取决于少子的浓度（计算时要用少子浓度）。

绘制 PN 结的平衡能带图：

画出统一的费米能级。
耗尽层以外部分的能带，和接触前相同。
耗尽层宽度与施主/受主掺杂浓度成反比，P 区能带较高，N 区能带较低。

5.3 异质结⚓

半导体异质结

将两种不同的半导体材料所组成的界面区称为异质结，如：在 \(\ce{GaAs}\) 衬底上外延生长合金半导体 \(\ce{Al_{x}Ga_{1-x}As}\)，在 \(\ce{InP}\) 衬底上外延生长 \(\ce{InGaAsP}\) 等。异质结具有许多普通 PN 结所没有的特性，常被用来改良半导体器件的性能。

与半导体同质结的区别

同质结由同种半导体材料构成。异质结由两种带隙宽度不同的材料组成。

异质结的分类（大写字母表示带隙更宽的材料）：

同型异质结：nN 型，pP 型。
异型异质结：Pn 型，pN 型。

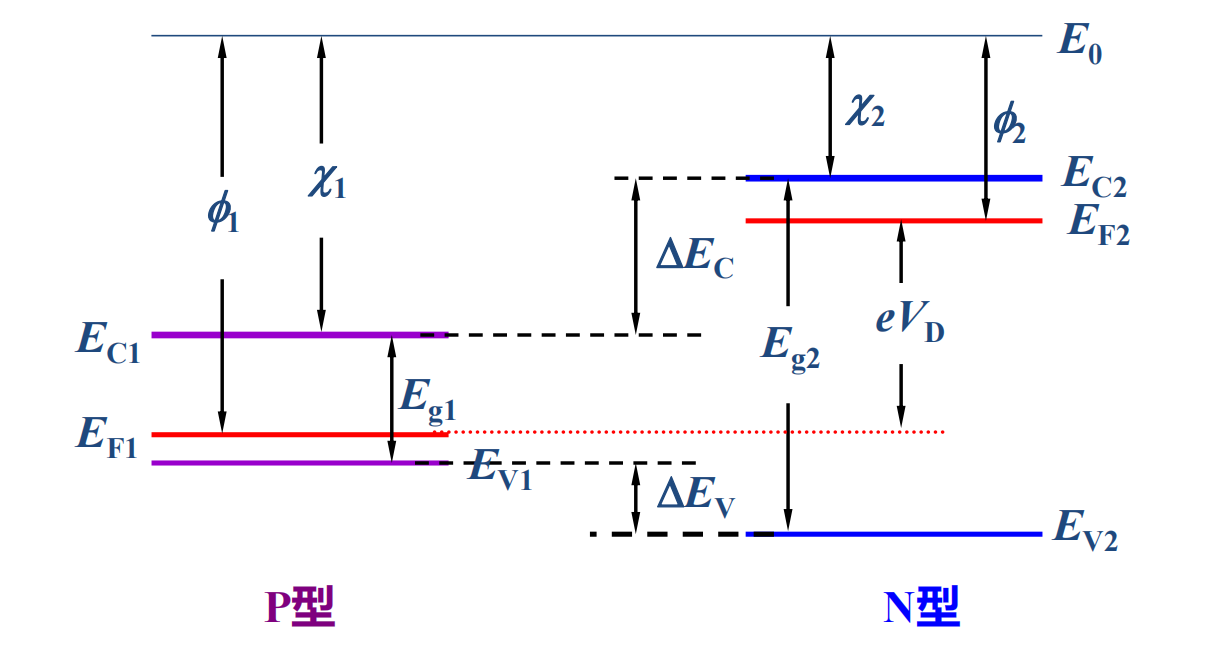
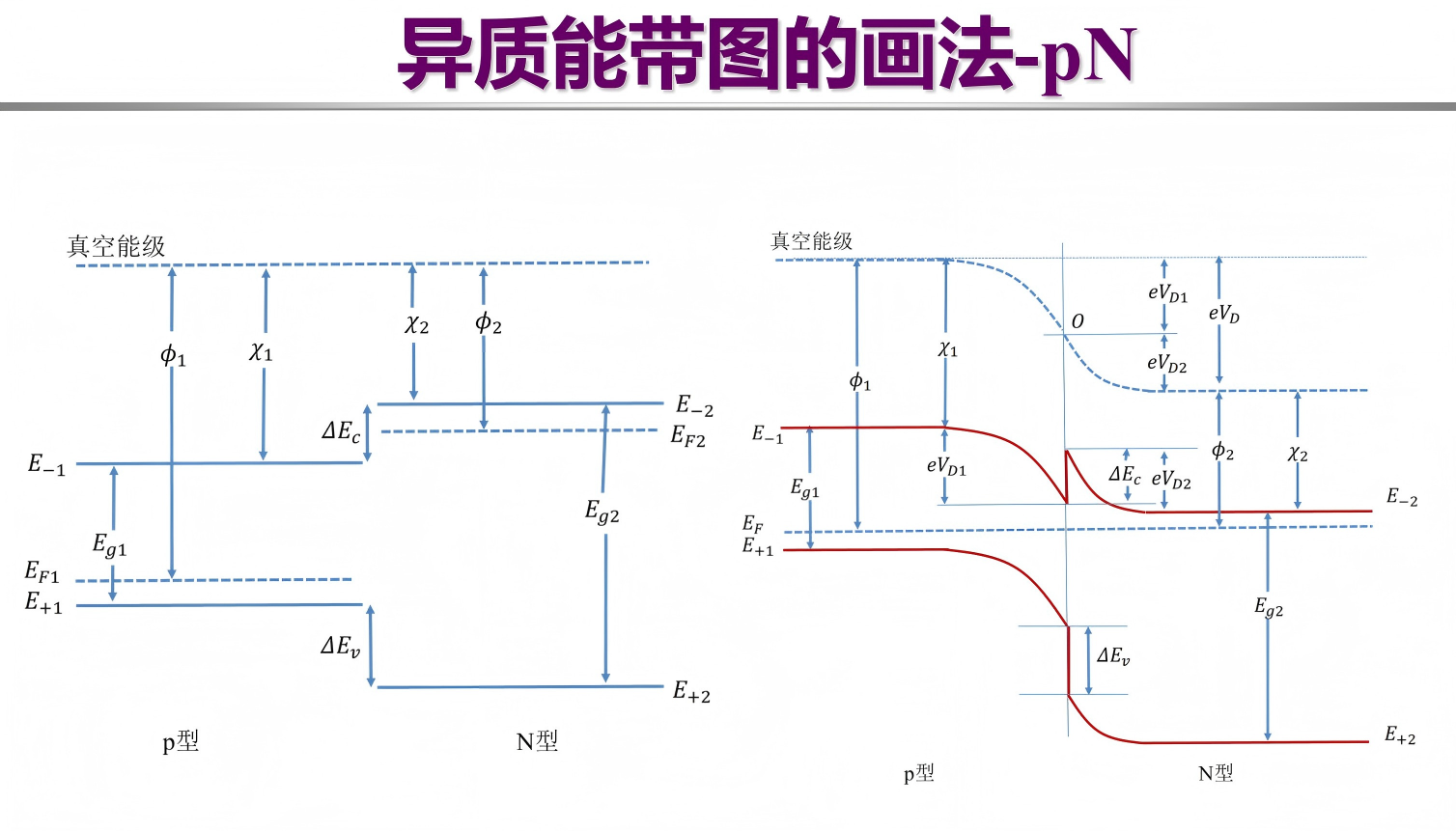
导带能级差等于材料亲合能之差 \(\Delta E_C=\chi_1-\chi_2\) 。

价带能级差等于带隙宽度差+导带能级差 \(\Delta E_V=(\chi_1+E_{g1})-(\chi_2+E_{g2})=E_{g1}-E_{g2}+\Delta E_C=\Delta E_C+\Delta E_g\) ，其中 \(E_g\) 为带隙宽度。

功函数差等于费米能级差的相反数 \(\Delta \phi=\phi_1-\phi_2=E_{F2}=E_{F1}=eV_D\) 。

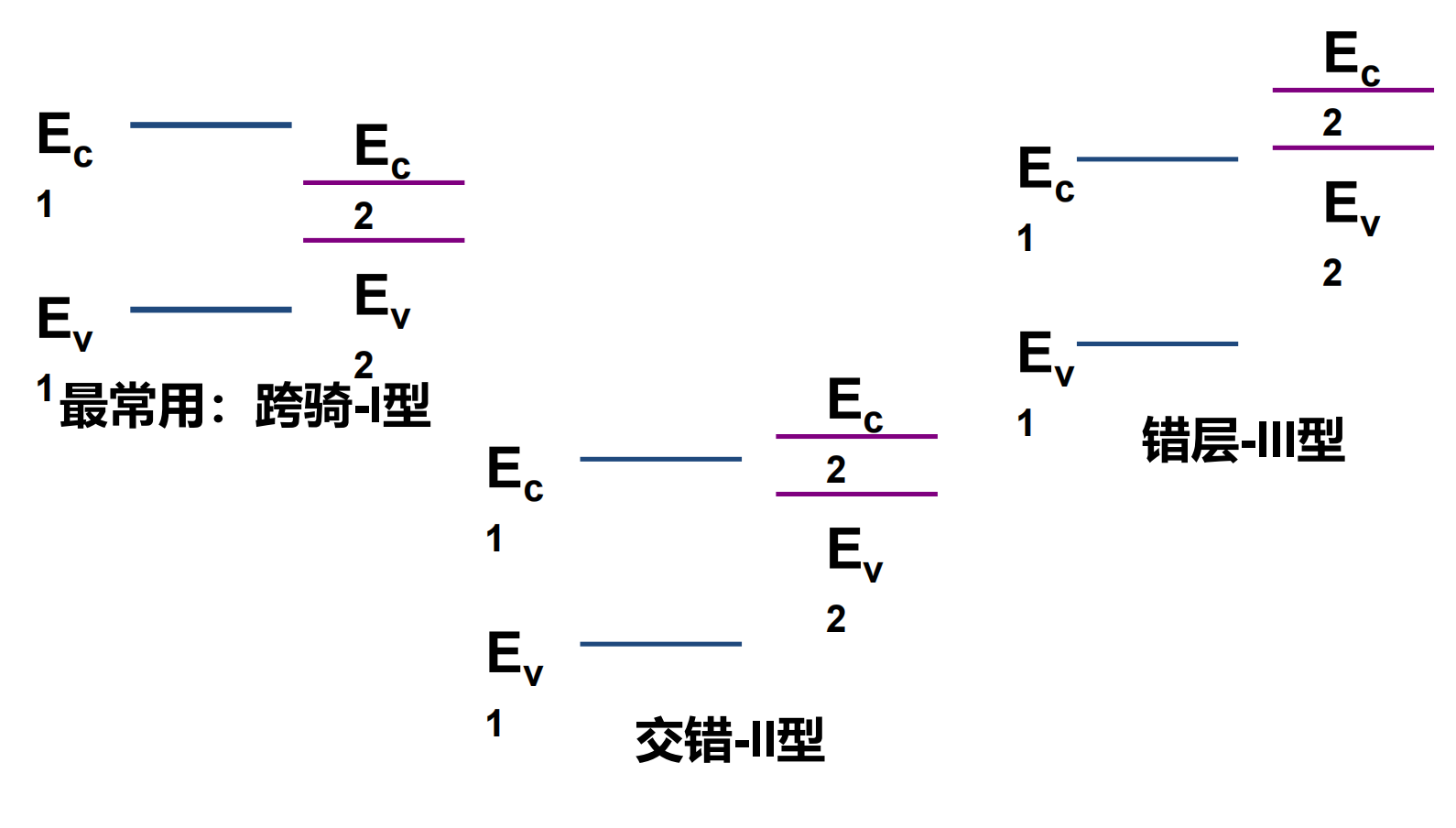
3种能带配合方式：

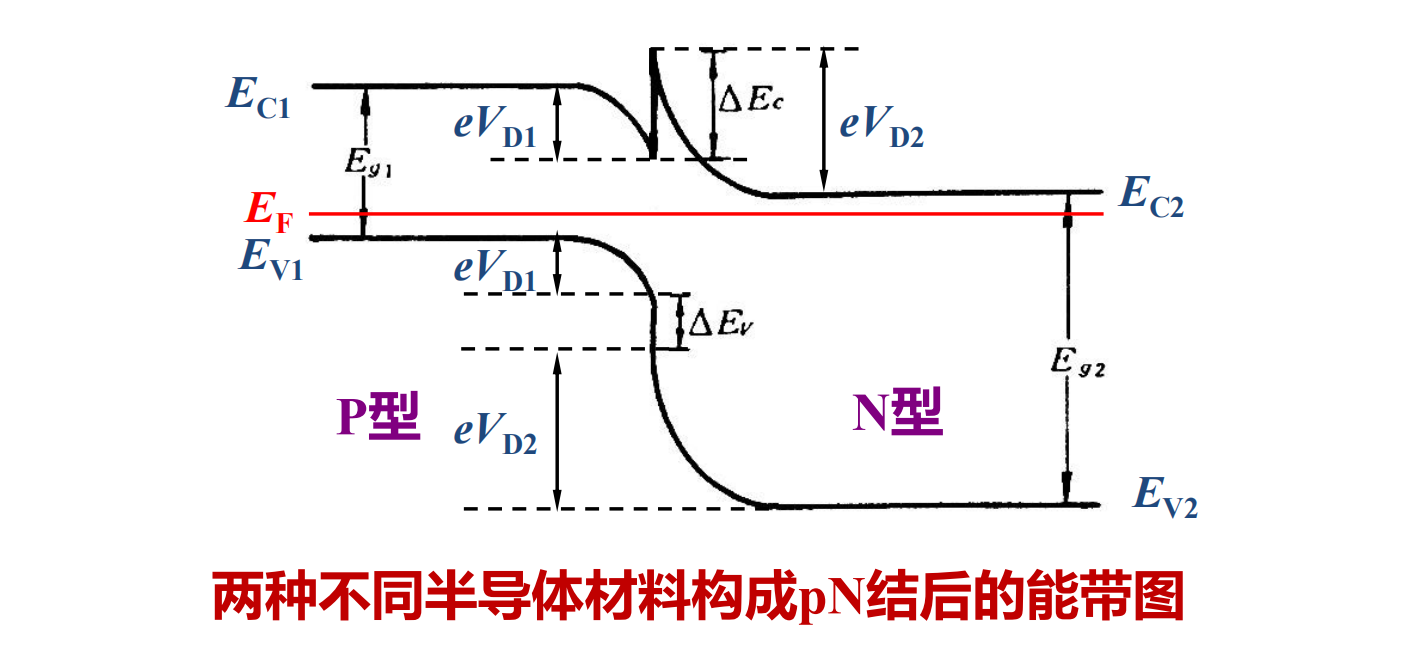
两种不同半导体材料构成 pN 结后的能带图：

电荷流动：电子从 N 区流向 P 区，空穴从 P 区流向 N 区。形成空间电荷区，内建电场从 N 区指向 P 区，将费米能级拉平。相当于 P 区能级整体平移，下降了 \(eV_D=E_{F2}-E_{F1}\) 。

能带在界面出现间断，上图中，p 区导带出现峡谷，N 区导带出现尖峰，峰谷差等于导带能级差。p 区和 N 区价带出现“台阶”，台阶差等于价带能级差。

pN 型异质结能带图的画法：

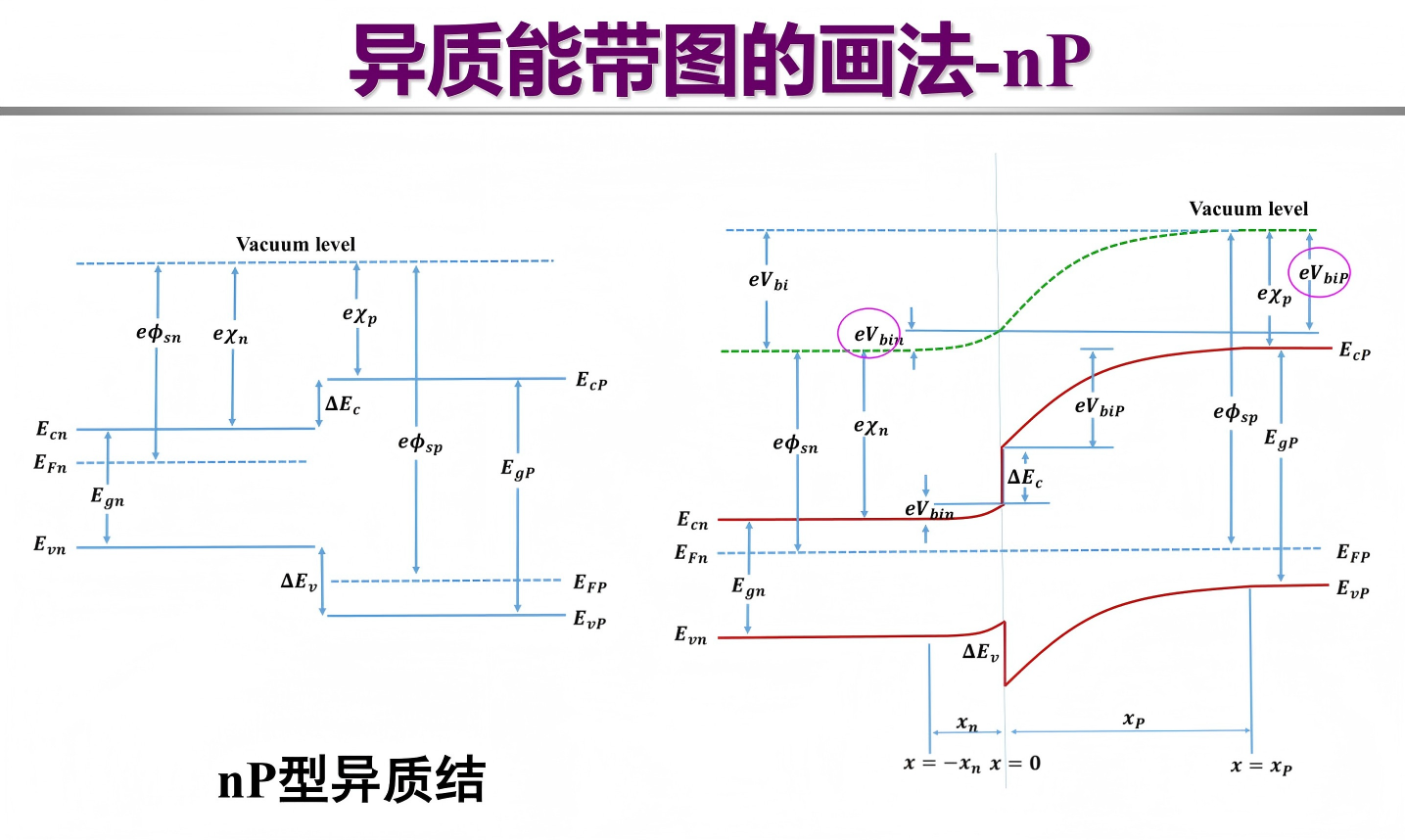
nP 型异质结能带图的画法：

关键：

确定能带弯曲的方向和保持能带差不变。
分界面有间断，界面处2种半导体的导带和价带4个点不变。
尖峰在 n 区或 N 区一侧，而尖峰在还是导带还是价带取决于类型，可以用极限法分析。
一般都是 p 区或 P 区整体上能级更高，n 区或 N 区更低。
其余和 PN 结类似。

注入比：总电流中，电子电流与空穴电流的比例。

同质 PN 结的注入比：

\[ \frac{j_n}{j_p} = \left(\frac{D_n n_p^0}{L_n}\right) \bigg/ \left(\frac{D_p p_n^0}{L_p}\right) = \frac{D_n L_p N_D}{D_p L_n N_A} \]

提高注入比的办法：同质结需要提高 N 区的施主杂质浓度，使得进入 P 区的电子数更多。

异质 PN 结具有很高的注入比，是“带隙宽度 \(E_g\) 之差”的指数形式增长：

\[ \frac{j_n}{j_p} = \left(\frac{D_n n_p^0}{L_n}\right) \bigg/ \left(\frac{D_p p_n^0}{L_p}\right) = \frac{D_n L_p N_D}{D_p L_n N_A} \exp\left(\frac{E_{gN} - E_{gP}}{k_B T}\right) \]

异质结构的优点：N 区的带隙宽度比 p 区带隙宽度大，可以进一步以指数级别增加注入比。提高注入比的意义：提高晶体管放大系数，例如异质结双极晶体管(HBT)。

异质结双极晶体管

在宽禁带的 \(\ce{AlGaAs}\) 中掺入施主杂质，\(\ce{GaAs}\) 材料不掺杂。电子将从 \(\ce{AlGaAs}\) 转移到 \(\ce{GaAs}\) ，在 \(\ce{AlGaAs}\) 一侧形成耗尽层， \(\ce{GaAs}\) 一侧有电子积累，构成调制掺杂异质结构。

此时在费米能级下方形成“负电子云”，电子被限制在窄的势阱中，尺度在 \(10\,\text{nm}\) 左右。垂直界面的方向，电子运动是量子化的，平行界面的方向，电子运动是自由的，属于一种二维电子气。 \(\ce{GaAs}\) 形成很高的电子浓度，但是不含有电离施主杂质，电子与电离施主在空间分离，电子受电离杂质散射几率减弱，载流子迁移率大为提高。

异质结双极晶体管的结构特点是具有宽带隙的发射区，大大提高了发射结的载流子注入效率。 \(\Delta E_g\) 的存在允许基区比发射区有更高的掺杂浓度，因而可以降低基极电阻，减小发射极-基极电容，从而能得到高频、高速、低噪声的性能。由于 \(\Delta E_g>0\) 并且有一定的范围，所以电流增益也很高。适合在低相位噪声振荡器、高效率功率放大器、宽带放大器中应用。

例如：\(\ce{SiGe}\) 异质结双极晶体管、 \(\ce{GaAlAs/GaAs}\) 异质结晶体管，NPN 型 \(\ce{InGaAsP/InP}\) 异质结双极晶体管，NPN 型 \(\ce{AlGaN/GaN}\) 异质结双极晶体管等。

5.4 金属-半导体结⚓

3种主要的金属-半导体接触方式：

肖特基势垒(Schottky barrier)，与 PN 结相似。
欧姆接触(Ohmic contact)，与电阻相似。
MOS 接触(Metal-Oxide-Semiconductor contact)。

Tip

金属可以看做掺杂浓度极高的半导体，因此金属-半导体接触时，只有半导体耗尽；金属-金属接触时，耗尽层基本没有。

肖特基势垒-肖特基结⚓

一般金属的功函数大于半导体，典型功函数(单位伏特 \(\text{V}\))：

金属：\(\ce{Al}\) 4.28, \(\ce{Au}\) 5.1, \(\ce{Pt}\) 5.65。

半导体：\(\ce{Si}\) 4.01, \(\ce{Ge}\) 4.13, \(\ce{GaAs}\) 4.07。

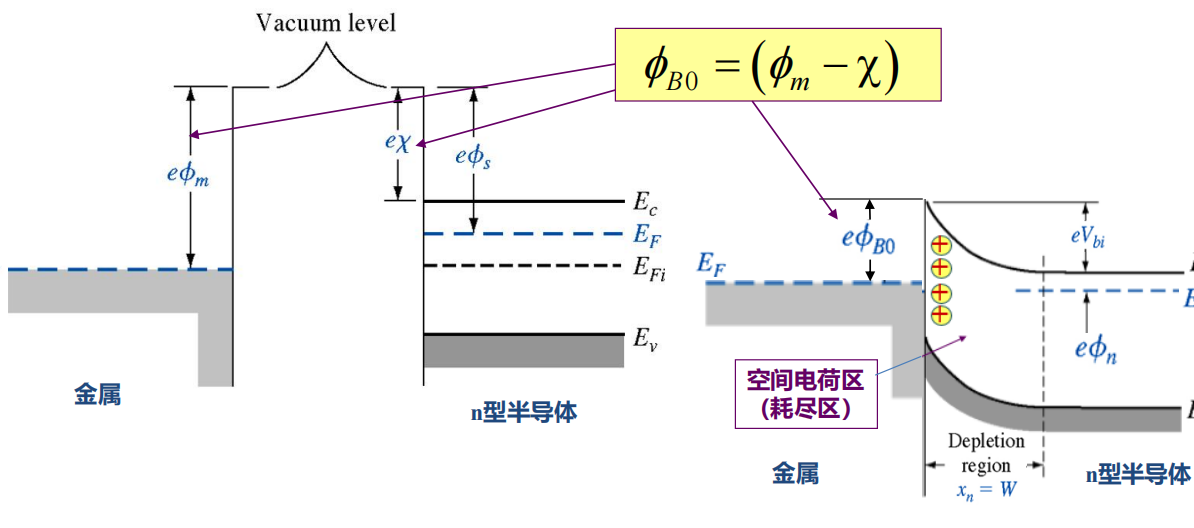
金属-n型半导体肖特基接触：

接触前，金属的功函数 \(\phi_m\) 大于半导体的功函数 \(\phi_s\) 。这也是“金属-n型半导体”肖特基接触的形成条件。

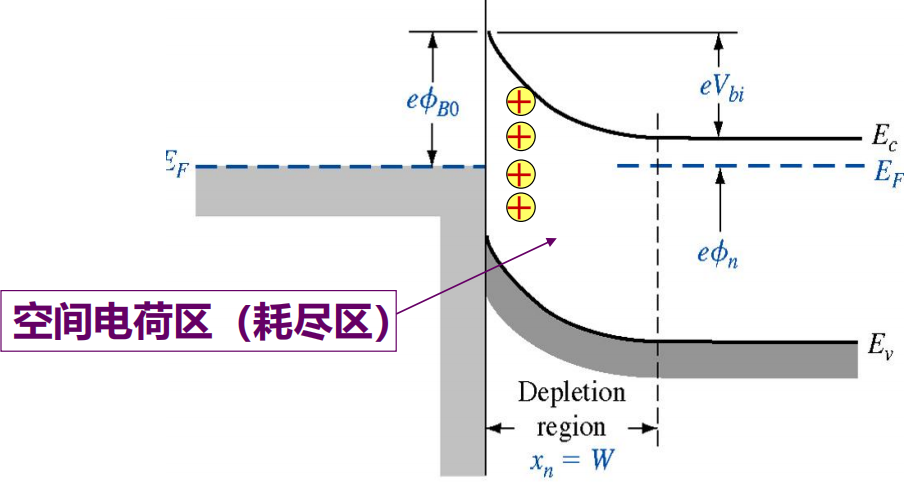
接触后，仍然是费米能级拉平，热平衡下，电子流向能量更低的金属，带正电荷的施主离子留下，形成空间电荷区（耗尽区）。从“金属-n型半导体”变为“金属-(p)-n型半导体”。

金属一侧形成的肖特基势垒 \(e\phi_{B0}=e(\phi_m-\chi)\) ，是金属功函数与半导体电子亲和能之差，阻止金属电子向半导体运动。

半导体一侧形成内建电势差 \(V_{bi}\) ，势垒 \(eV_{bi}=e(\phi_{B0}-\phi_n)\) ，阻止导带电子向金属运动。

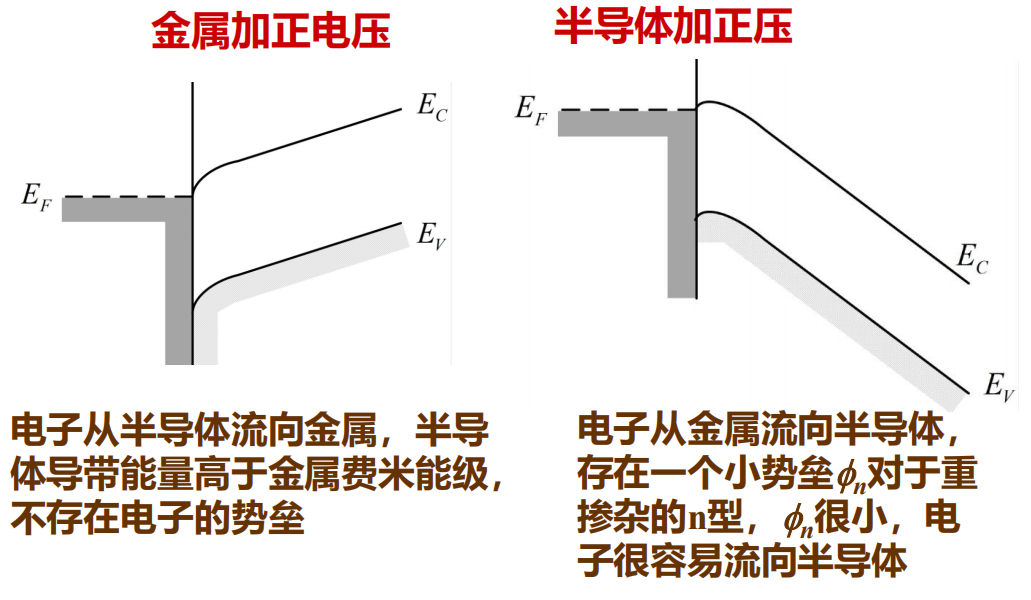
加偏压“n型半导体到金属方向”，半导体到金属的势垒高度增加，金属功函数 \(e\phi_{B0}\) 不变，电子从金属流向半导体需要越过势垒。

加偏压“金属到 n型半导体方向”，半导体到金属的势垒高度减小， \(\phi_{B0}\) 不变，电子很容易从半导体流向金属。

欧姆接触⚓

指金属与半导体的接触，而其接触面的电阻值远小于半导体本身的电阻，不产生明显的附加阻抗，而且不会使半导体内部的平衡载流子浓度发生显著的改变。即满足：

金属与半导体接触，但不形成肖特基结。
接触电阻很低，双向都形成电流接触。
理想情况下，电流与电压成正比，电压很低。

形成条件：金属的功函数较小，使得势垒接近于0，即 \(\phi_m\approx \chi\) 。

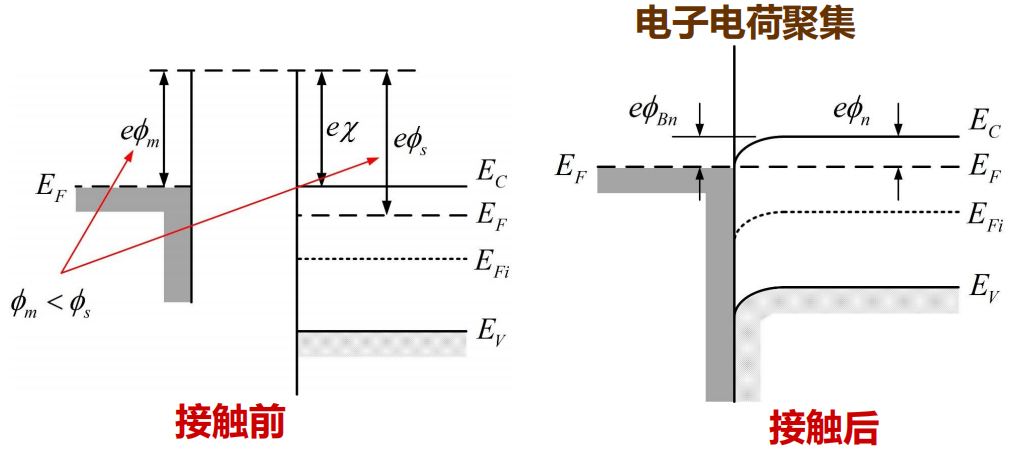
金属-n型半导体欧姆接触，形成条件 \(\phi_m<\phi_s\) ：

为了达到热平衡，电子从金属流向半导体，半导体更加趋向 N 型，界面处在界面有电子电荷聚集。

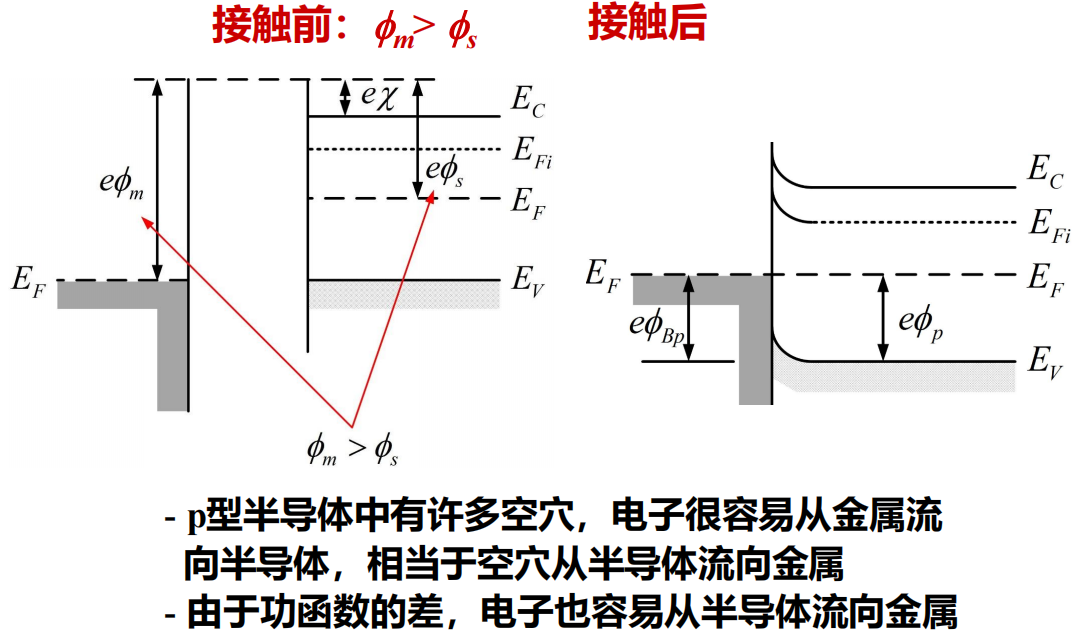
金属-p型半导体欧姆接触，形成条件 \(\phi_m>\phi_s\) ：

总结⚓

肖特基接触：（金属费米能级不变，半导体费米能级与金属对齐）

金属-n 型：金属的功函数更大，费米能级更低。
金属-p 型：金属的功函数更小，费米能级更高（不常见，因为一般金属的功函数大于半导体）。
平衡：载流子双向热发射达到平衡。
偏压：改变半导体侧势垒高度和耗尽层宽度，打破平衡。

欧姆接触：（与肖特基接触在能级性质上相反）

金属-n 型：金属的功函数更小，费米能级更高。
金属-p 型：金属的功函数更大，费米能级更低。

5.5 金属-绝缘体-半导体系统⚓

以 P 型半导体衬底为例，栅极加以负电压，将吸收空穴到半导体表面，使表面形成带正电荷的空穴积累层。

当栅压为正，即有从 P 型半导体表面排斥多数载流子空穴的作用，又有吸引少数载流子电子到半导体表面的作用。

当正栅压较小时，主要是 P 型半导体表面的空穴被赶走，形成带负电荷的耗尽层。空间电荷区可屏蔽栅压引起的电场，空间电荷区中存在的电场引起电势的变化，使能带弯曲向下，形成空穴势垒。

当正栅压较大时，表面势增强足够大时，表面处的费米能级有可能进入带隙上半部，这时在表面的电子浓度将超过空穴浓度，从而形成电子导电层，其载流子和体内导电型号相反，称为反型层。反型层中的电子实际上被限在表面附近能量最低的一个狭窄区域，因此反型层有时也称为沟道。P 型半导体的表面反型层是由电子构成的，所以也称为 N 沟道。

N 型 MOS 场效应管

源区和漏区之间相当于两个背靠背的 pn 结，即使加电压，也只有反向饱和电流。栅极加以正偏压，超过阈值形成反型层，作为 n 沟道，再在源极和漏极间加以电压，则有较明显的电流产生。即通过控制栅极电压，可控制源、漏之间的通断。

MOS 场效应管是单极型器件，沟道中参加导电的主要是多数载流子，相比之下易于控制，热稳定性好，抗辐射能力强。

CMOS 集成电路(Complementary Metal Oxide Semiconductor)，用 P 沟道 MOS 管作为负载器件，N 沟道 MOS 管作为驱动器件，因此在同个衬底上同时制作 P 沟道 MOS 晶体管和 N 沟道 MOS 晶体管。在制作中，必须将一种 MOS 晶体管制作在衬底上，而将另一种 MOS 晶体管制作在比衬底浓度高的阱中。CMOS 集成电路工艺根据阱的导电类型可以分为 P 阱工艺、N 阱工艺和双阱工艺。

第五章 固体间接触的电特性⚓