第七章 图像校正和修补⚓
本章概述
恢复像素的位置和灰度的两类技术——几何失真校正和图像缺损修补。
几何失真是像素位置（相对于原始场景）发生改变的结果。
图像缺损可以看作是像素的灰度改变或丢失的结果。
7.1 基本坐标变换⚓
二维平面上的齐次坐标 \([x,y,1]^T\) ，直线可表示为 \(l=[a,b,c]^T\)，点位于直线上等价于两个矢量的内积为0：\([x,y,1][a,b,c]^T=ax+by+c=0\) 。
变换的表达：
7.1.1 基本坐标变换⚓
平移变换，变换矩阵：
放缩变换，变换矩阵：
旋转变换，绕 Z 轴旋转，变换矩阵：
若旋转轴不在原点，则：绕非原点旋转 = 平移至原点 + 绕原点旋转 + 平移回去。
镜像变换，水平镜像的变换矩阵为：
竖直镜像的矩阵同理。可见镜像变换是放缩变换的一个特例。
7.1.2 坐标变换扩展⚓
反变换：
变换的级联，\(v'=R_\gamma[S(Tv)]=Av\) ，本质是若干矩阵相乘得到一个矩阵，注意级联的运算次序不可交换。
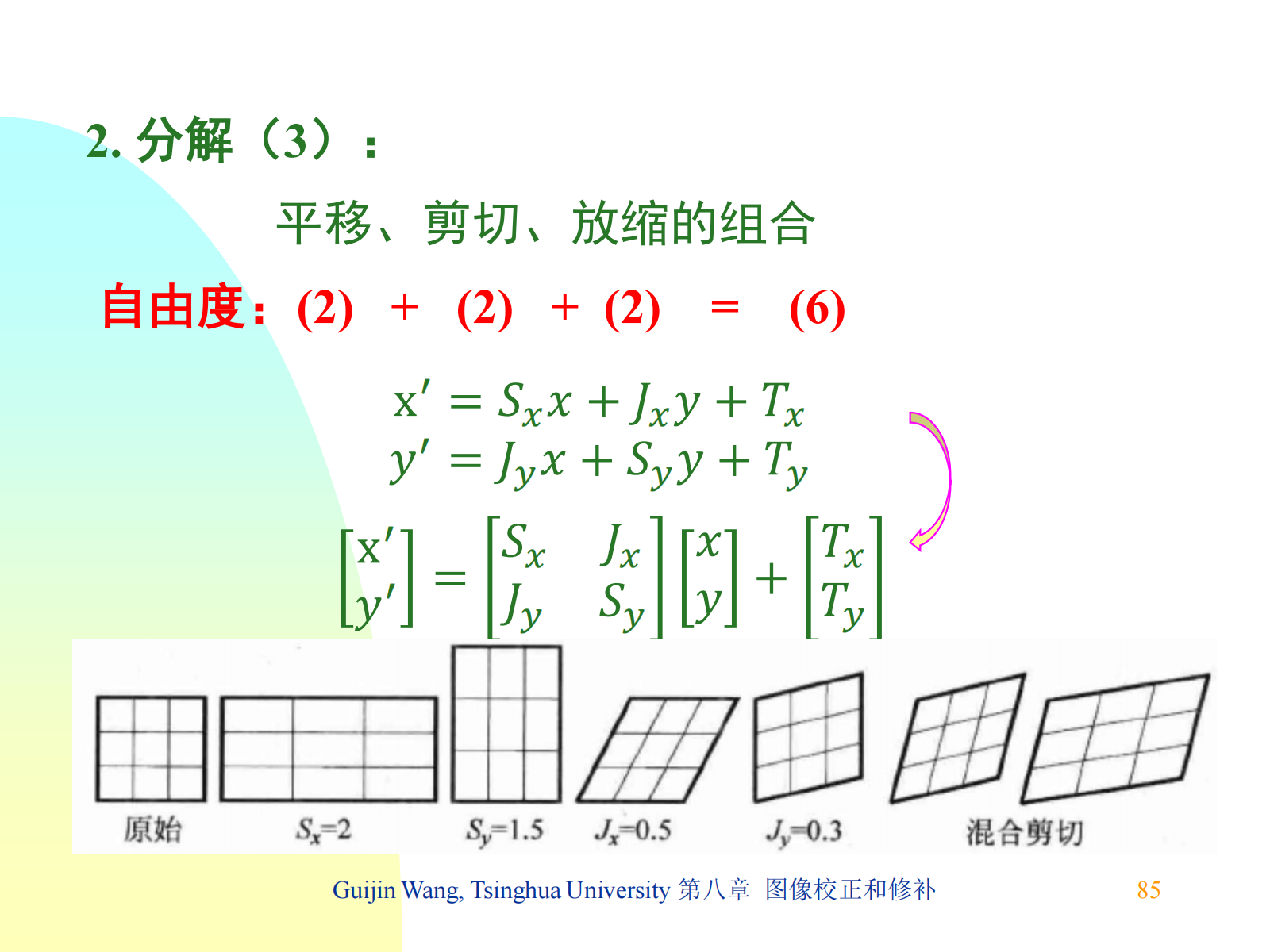
拉伸变换，变换矩阵（一个方向放大一个方向缩小，理论上面积不变。也可看作放缩变换的一个特例）：
剪切变换，变换矩阵：
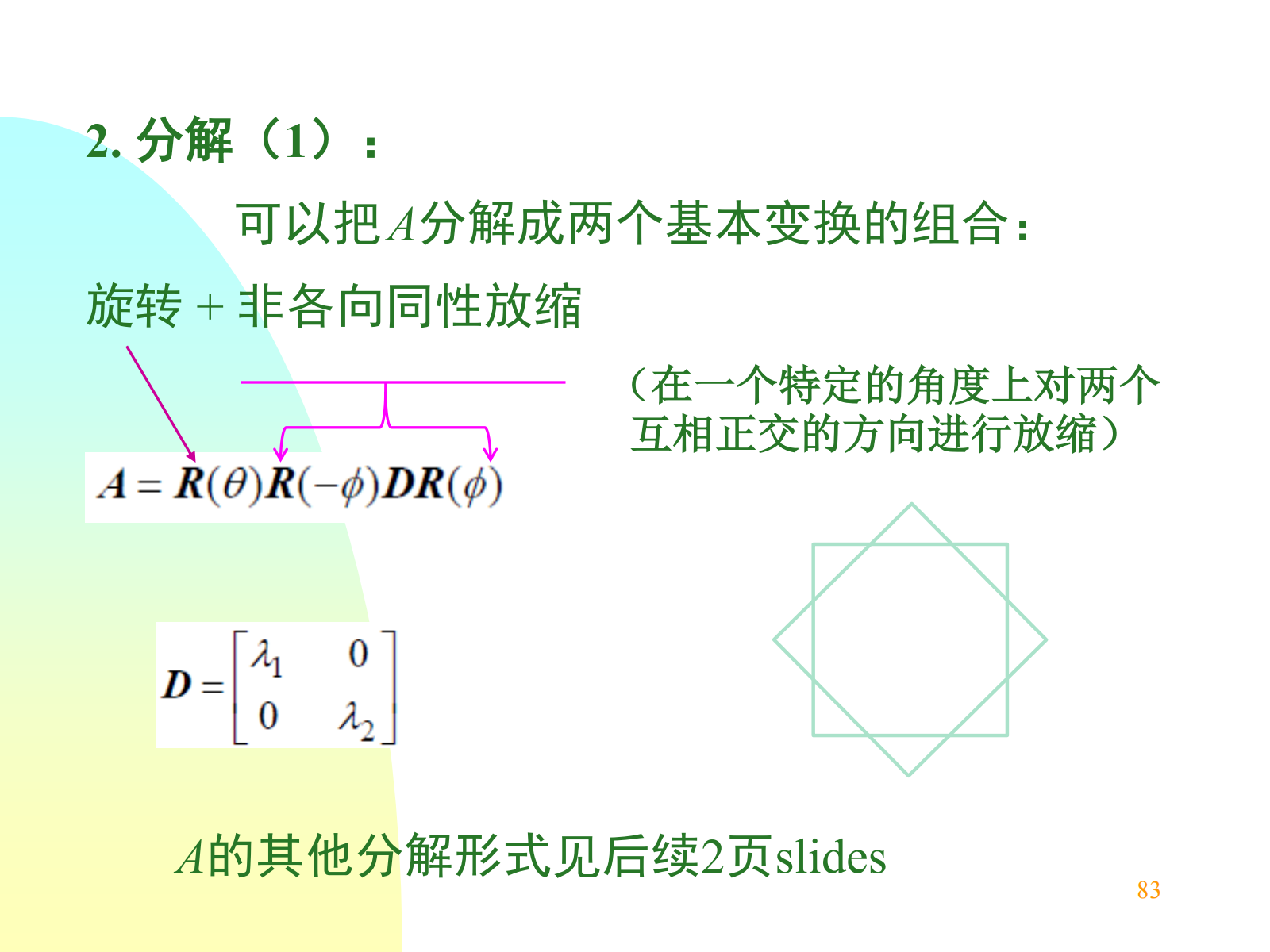
旋转变换的分解：
(1) 旋转 = 垂直剪切放缩 + 水平剪切放缩：
(2) 旋转 = 水平剪切 + 垂直剪切 + 水平剪切：
7.2 图像仿射变换⚓
7.2.1 一般仿射变换⚓
一般仿射变换：一个非奇异线性变换接一个平移变换。平面上的仿射变换有6个自由度。
性质：
- 仿射变换将有限点映射为有限点，即仿射变换能建立一对一的关系。
- 仿射变换仍将直线映射为直线。
- 仿射变换将平行直线映射为平行直线。
- 如果区域 P 和 Q 是没有退化的三角形（即面积不为0），那么存在一个唯一的仿射变换 A 可将 P 映射为 Q，即 \(Q = A(P)\) ，3点可决定一个仿射变换。
- 仿射变换会导致区域面积变化。
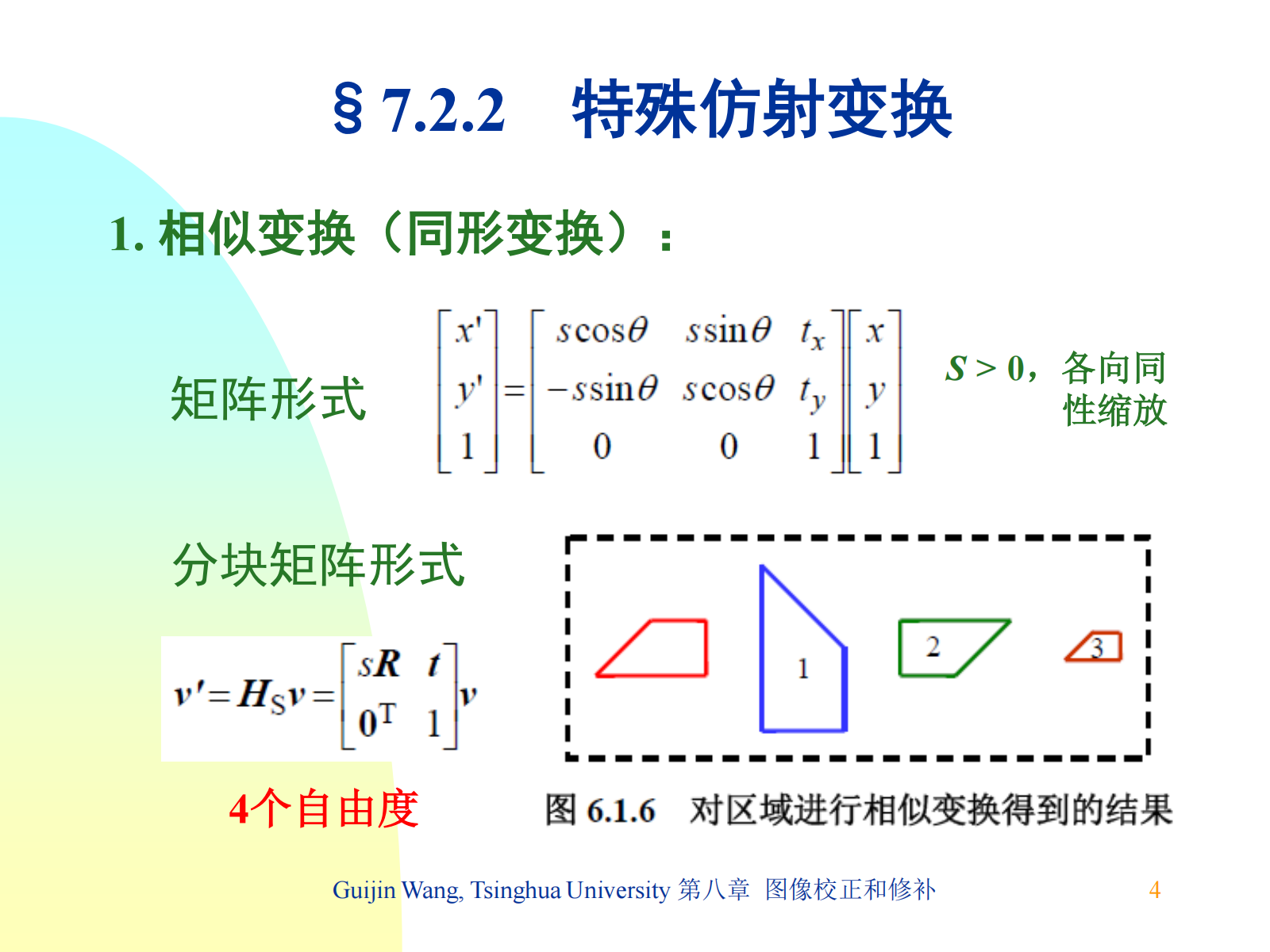
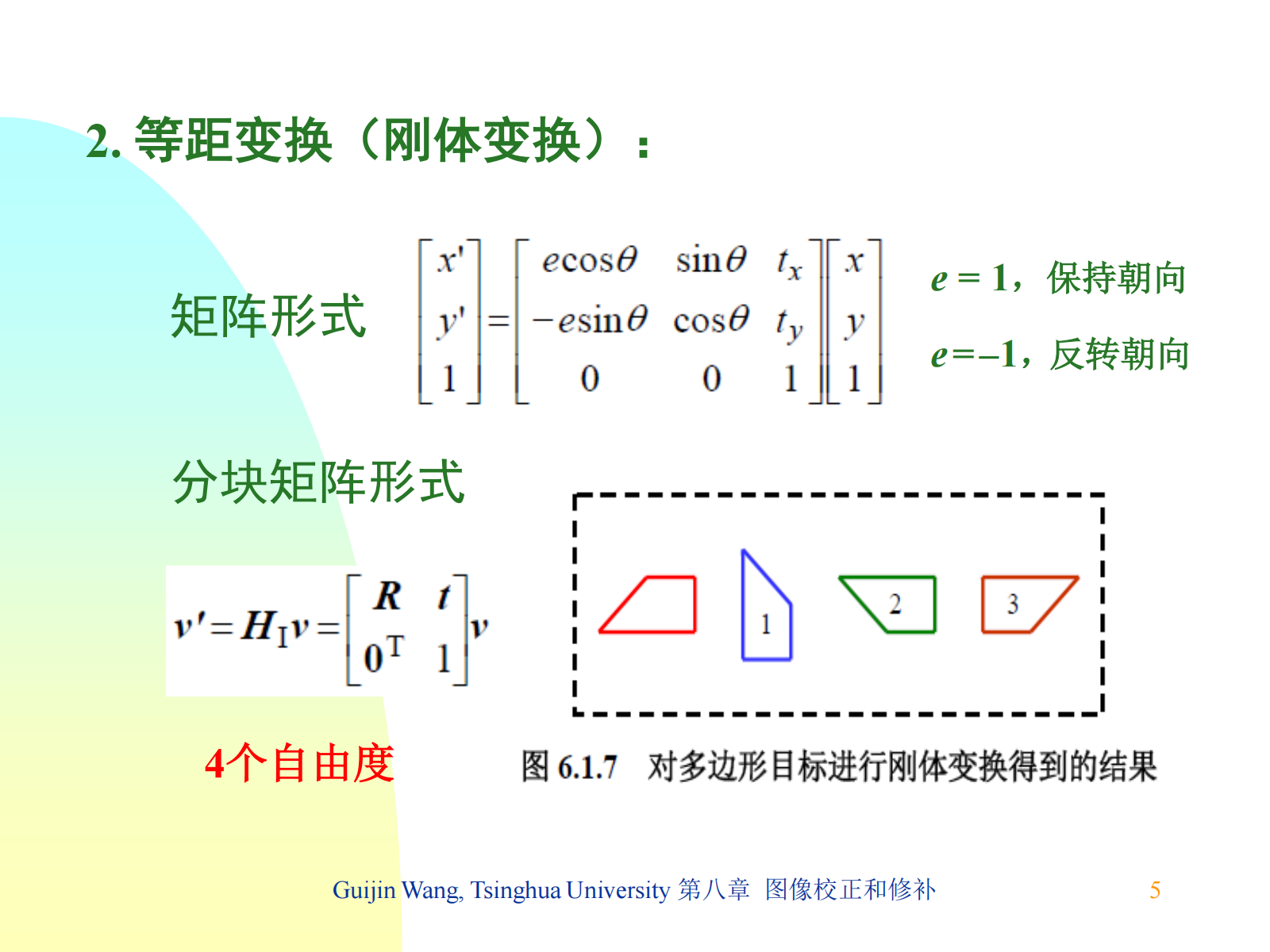
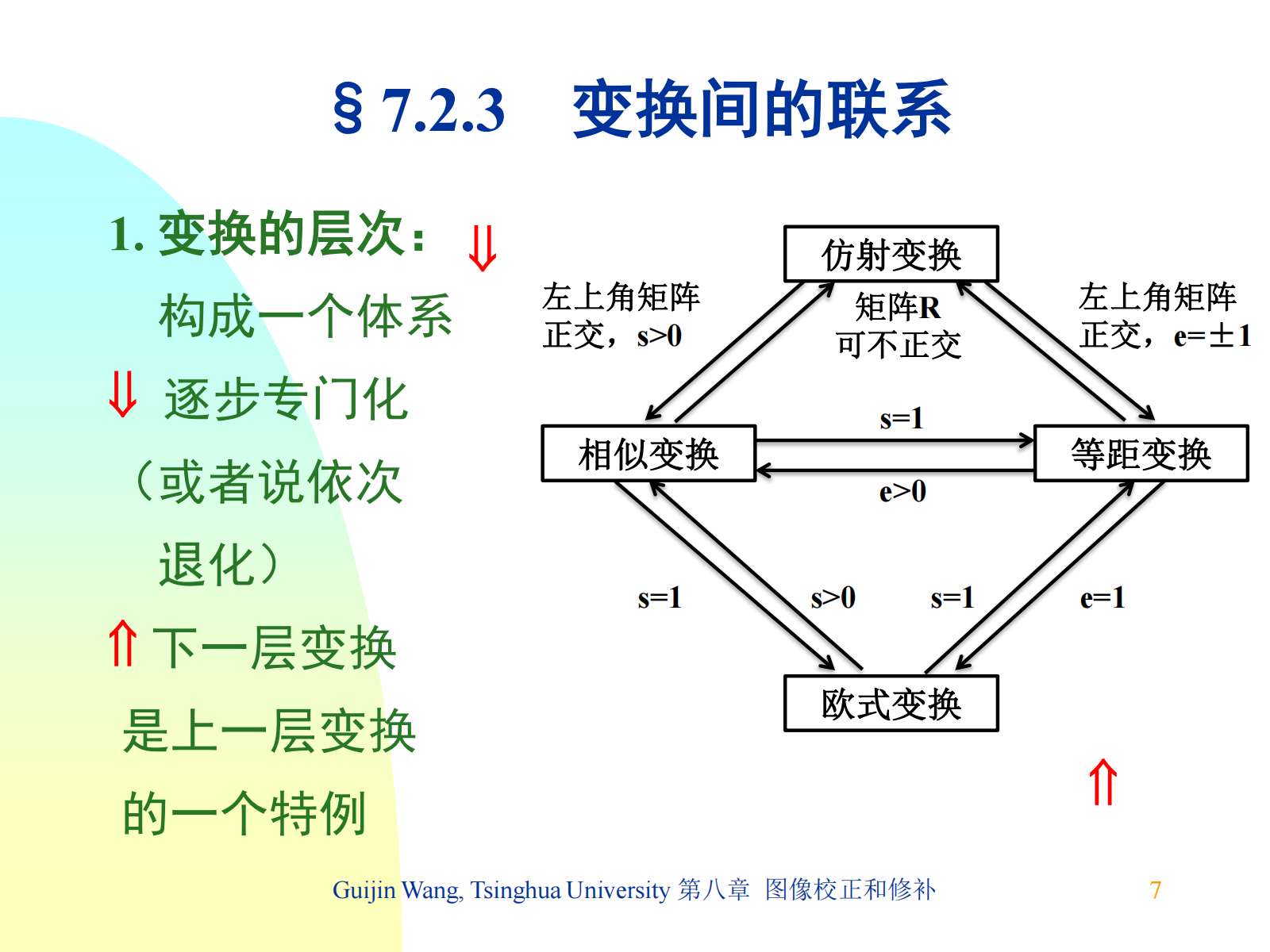
7.2.2 特殊仿射变换⚓
几种变换的对比：
| 变换 | 仿射 | 相似 | 等距 | 欧式 |
|---|---|---|---|---|
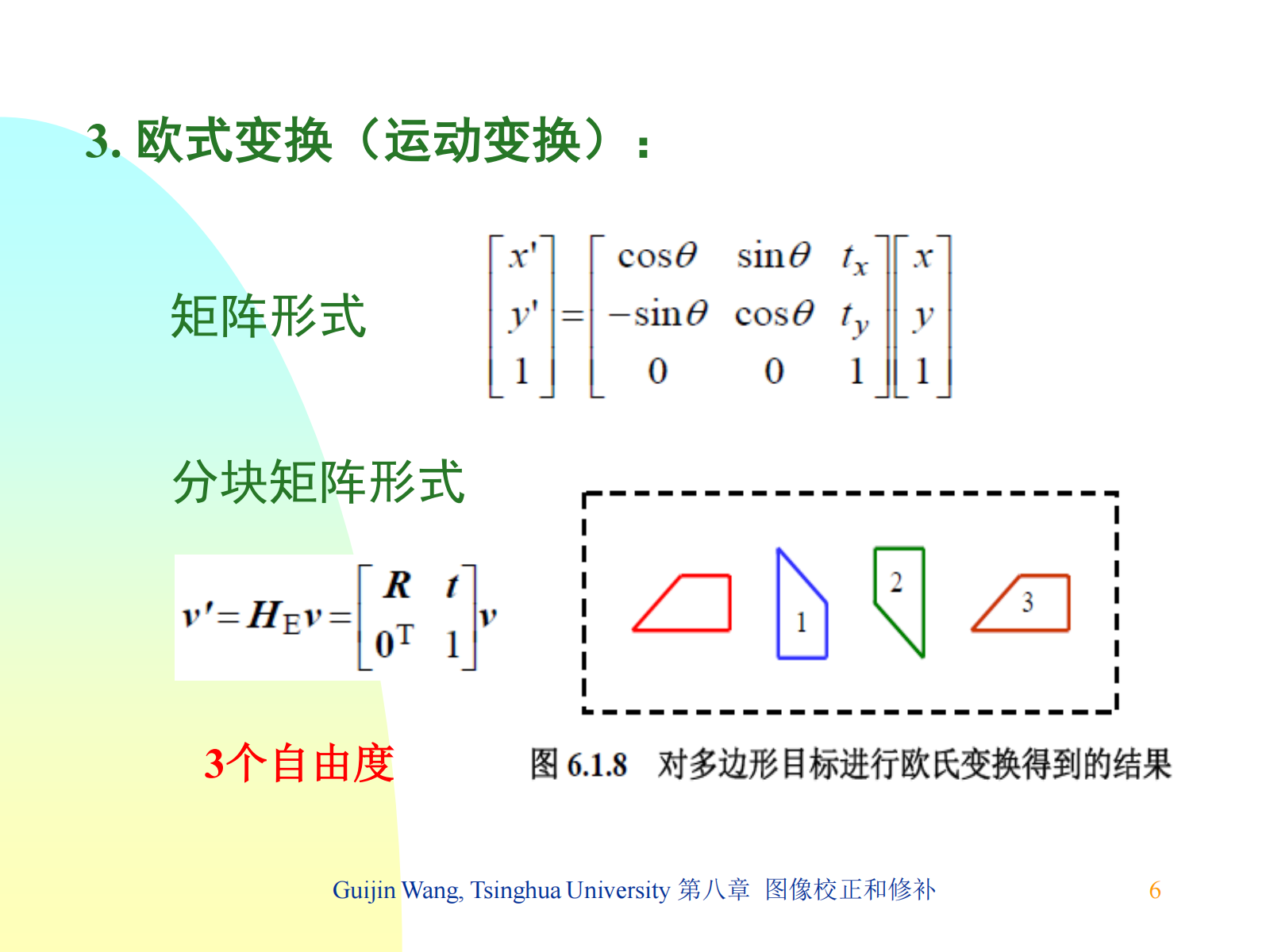
| 自由度 | 6 | 4 | 4 | 3 |
| 计算所需点数 | 3 | 2 | 3 | 2 |
| 分解 | 平移、旋转、非各向同性放缩 | 平移、旋转、各向同性放缩 | 平移、旋转、翻转 | 平移、旋转 |
| 失真 | 圆→椭圆，方→平行四边形 | 圆→圆，方→方 | 圆→圆，方→方 | 圆→圆，方→方 |
| 不变量 | 平行线段长度比，区域面积比 | 夹角角度，线段长度比，区域面积比 | 夹角角度，线段长度，区域面积 | 夹角角度，线段长度，区域面积 |
| 不变性 | 直线平行性 | 保形（保角） |
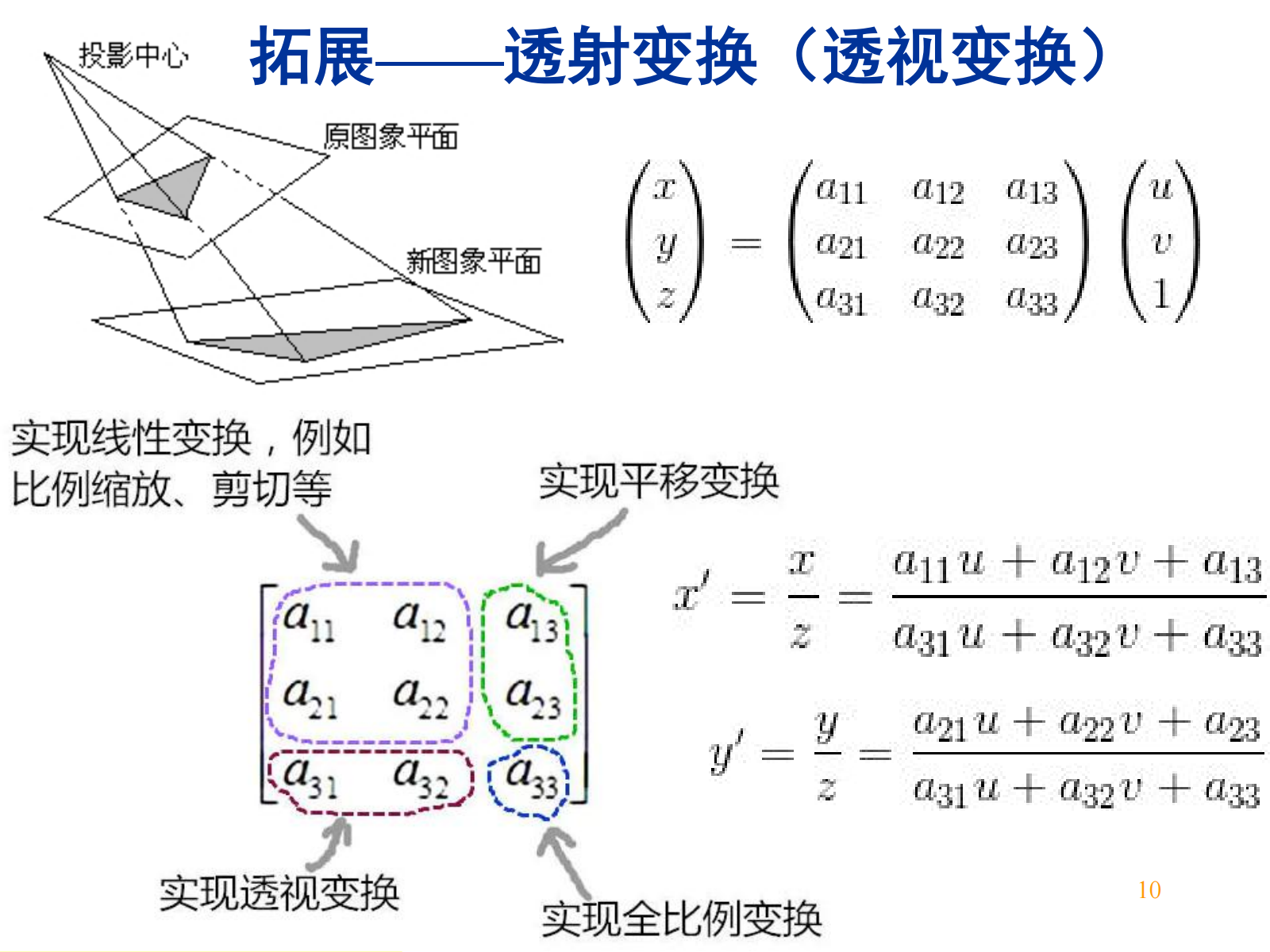
7.2.3 透视变换⚓
透视变换(Perspective Transformation)是将图片投影到一个新的视平面(Viewing Plane)，也称作投影映射(Projective Mapping)。利用透视中心、像点、目标点三点共线的条件，按透视旋转定律使承影面（透视面）绕迹线（透视轴）旋转某一角度，破坏原有的投影光线束，仍能保持承影面上投影图形拓扑结构不变的变换。
7.3 几何失真校正⚓
实际的图像采集过程中，图像中像素之间的空间关系会发生变化，即图像产生了几何失真或几何畸变。几何失真校正处理步骤：
- 空间变换：对图像平面上的像素重新排列，以恢复原有的空间关系。
- 灰度插值：对空间变换后的像素赋予相应的灰度值，以恢复原位置的灰度值。
7.3.1 空间变换⚓
设原图像 \(f(x, y)\)，几何失真图像 \(g(x', y')\) ，失真图像坐标可表示为：
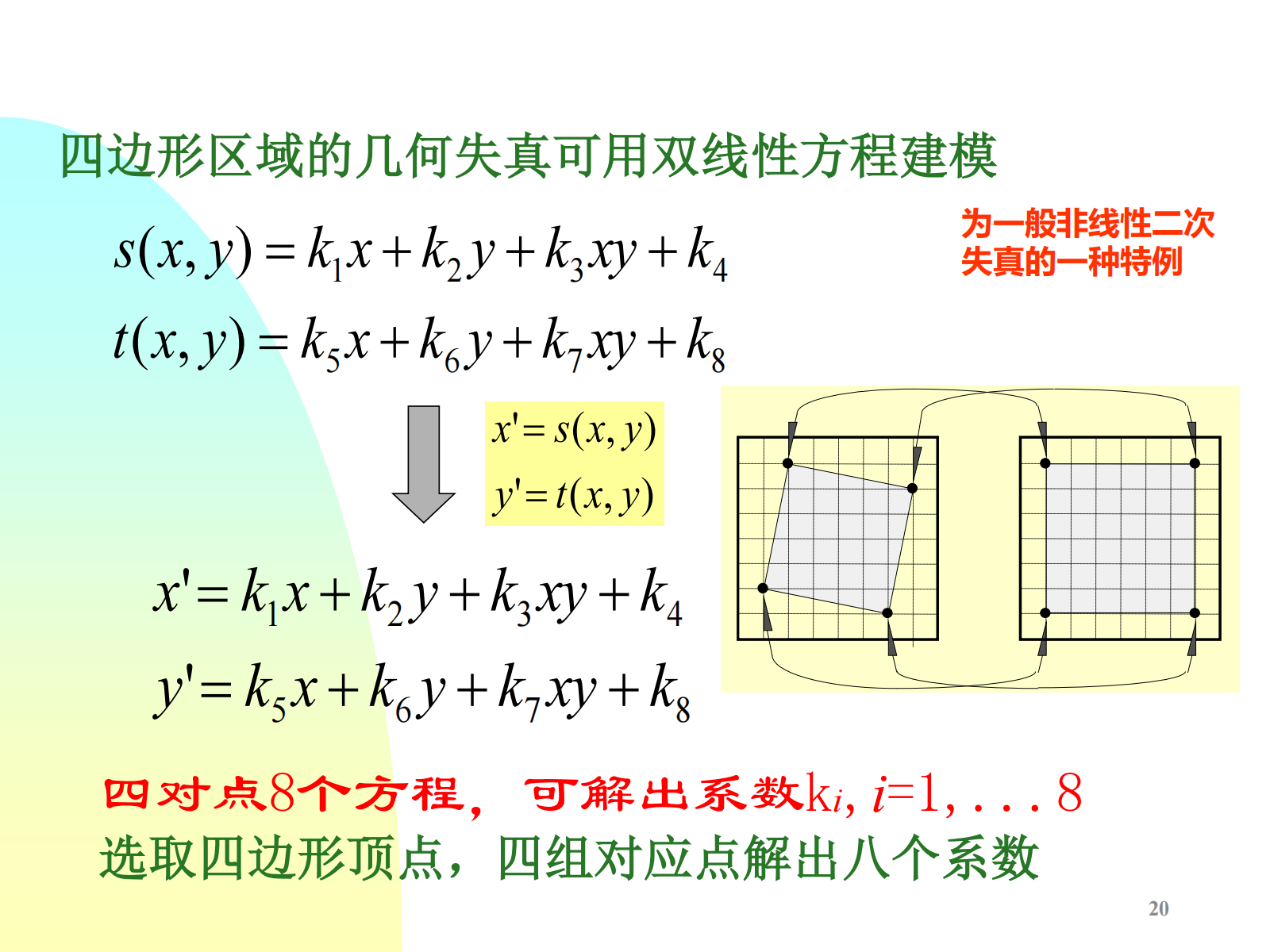
最简单的情况，\(s, t\) 为产生失真的2个线性空间变换（一次）：
通常实际中无法事先知道 \(s,t\) 的解析表达式，所以需要在恢复过程中，找出输入图(失真图)和输出图(校正图)中的一些对应点，利用对应点建立其他像素的空间对应关系。
由求得的系数 \(k_i\) 可对四边形区域所有点的位置进行空间变换，从而恢复原图像形状。通常对图像的几何失真校正，都是将图像分成四边形集合，然后对每个区域校正完成。
应用：图像拼接
选取两幅画面主体部分基本一致、只是拍摄角度相异的图片。通过对一幅图像进行仿射变换，使得相同的主体部分能够重合，达成对两幅图进行拼接的效果，获得一幅画面视角更广阔的图。
图像特征点可以用来表征图像内容：运动目标追踪，物体识别与匹配，图像配准与拼接，标定与去畸变。
角点：局部窗口沿各方向移动，均产生明显变化的点，图像局部曲率突变的点。
Harris 角点检测：使用一个小窗口，在角点处，窗口向任意方向的移动都导致图像灰度的明显变化。
设窗函数为 \(w(x,y)\) (常用矩形窗或高斯窗)，灰度值为 \(I(x,y)\)， 将图像窗口平移 \([u,v]\) 产生灰度变化 \(E(u,v)\) ：
对于局部微小的移动量 \([u, v]\) ，可以近似得到：
其中 \(M\) 是 \(2 \times 2\) 矩阵，可由图像的导数求得（梯度的协方差矩阵）:
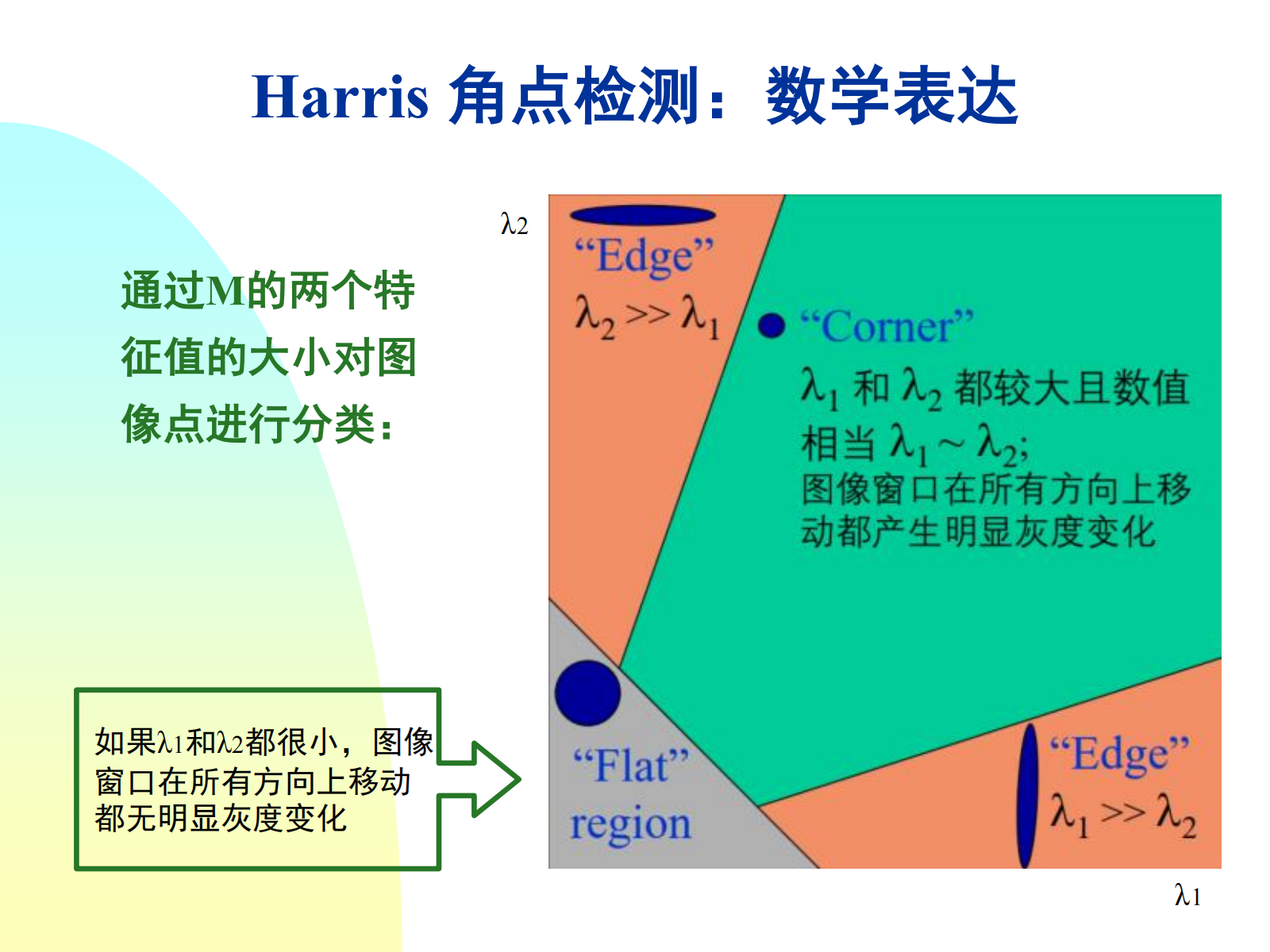
于是窗口移动导致的图像变化等价于实对称矩阵 \(M\) 的特征值分析。
定义：角点响应函数
\(k\) 为经验常数，一般取 \(0.04\sim0.06\)。\(R\) 只与 \(M\) 的特征值有关：
- 角点：\(R\) 为大数值正数。
- 边缘：\(R\) 为大数值负数。
- 平坦区：\(R\) 为小数值。
算法流程：
- 计算图像导数 \(I_x, I_y, I_{xy}\) 。
- 计算角点响应函数 \(R\) 。
- 对 \(R\) 进行阈值处理：\(R > \text{threshold}\) 。
- 提取 \(R\) 的局部极大值(非极大值抑制)。
Harris 角点性质：
- 旋转不变性。
- 对图像灰度的仿射变换具有部分的不变性。
- Harris 角点不具有尺度变换不变性(角点放大后可能变得平坦)。
7.3.2 灰度插值⚓
前向映射：
根据 \((x',y')\) 计算出 \((x,y)\) 。如果失真图像 \(g(x',y')\) 中的一个像素坐标 \((x',y')\) ，对应到不失真图像 \(f(x,y)\) 的4个像素之间(非整数点)，则将失真图像中像素灰度根据距离远近，分配给不失真图像的那4个像素中的1个。
存在的问题：
- 前向映射一定数量的失真图像坐标可能会映射到不失真图像之外，导致计算方面的浪费。
- 不失真图像中许多像素的灰度将由许多失真图像像素的贡献之和决定，需要较多的寻址。
- 不失真图像中有的像素可能得不到来自失真图像的赋值(产生孔洞)，而有些像素多次赋值。
后向映射：
根据 \((x,y)\) 计算出 \((x',y')\) 。如果不失真图像 \(f(x,y)\) 的一个像素坐标 \((x,y)\) ，对应到失真图像 \(g(x',y')\) 中的4个像素之间(非整数点)，则先插值计算出该位置的灰度 \(g(x',y')\) ，再映射给不失真图像的对应像素 \(f(x,y)\) 。
后向映射可以避免产生空洞，且效率较高。因为不失真图是逐个像素得到的，每个像素的灰度由一步映射决定。
插值方法：
- 最近邻插值，可能产生锯齿状边缘，不够平滑，但不会模糊，保留了锐度，适用于处理速度快的场景。
- 双线性插值，图像更平滑，但略有模糊，适用于需要较好视觉效果的场景。
- 双三次插值，视觉效果更好，但计算复杂度高。
7.3.3 相机标定⚓
桶形失真，枕形失真。
内参矩阵 \(A:3\times 3\) ，描述从相机坐标系到像素坐标系的变换，自由度为5。只与相机本身的几何/电子特性相关，对同一个相机拍出的任何照片都恒定不变。
外参矩阵 \([R|t]=[r_1,\; r_2,\;r_3,\;t]:3\times 4\) ，\(R\) 为旋转矩阵， \(t\) 为平移向量，总自由度为6。通常省略 \(r_3\) 因为设定棋盘格点都位于 Z=0 平面上。随相机相对于世界的姿态而变，每拍一张图都不同。
在设定标定平面 \(Z=0\) 时，单映性矩阵 \(H=A[r_1,\; r_2,\;t]:3\times 3\) ，直接描述从世界坐标系到像素坐标系的的变换。由于使用齐次坐标，可以任意缩放，因此具有8个自由度，通常设置约束条件为矩阵 H 的模为1。
约束条件：旋转矢量正交且模长相等 \(r_1^T r_2=0,\;r_1^T r_1=r_2^T r_2\) 。带入可得，每个单映性矩阵可以得到内参矩阵的2个约束，因此至少需要3个棋盘位姿解得内参的5个参数，获得 \(A\) 之后根据单映性矩阵可以得到外参（单映性矩阵需要两个图片的4对点求出）。通常选择10-20个棋盘位姿，保证较好的条件约束，使数值计算结果稳定。
7.4 图像修复⚓
图像中部分区域发生缺损或缺失，像素灰度急剧改变，使图像不完整的情况：
- 在采集有遮挡的场景图像或扫描有破损的老图片时产生的部分内容的缺失。
- 在图像加工中去除特定区域（无关景物）后留下的空白。
- 图像上覆盖文字或受到干扰（照片撕裂或有划痕）导致的变化。
- 对图像进行有损压缩时而造成的部分信息丢失。
- 在（网络上）传输数据时由于网络故障所导致的像素丢失。
7.4.1 图像修补原理⚓
图像修补：基于不完整的图像和对原始图像的先验知识，通过采用相应的方法纠正或校正前述区域缺损问题，以达到恢复图像原貌的目的。
修复（插补）：修补尺度较小的区域，多利用局部结构信息。
补全（填充）：修补尺度较大的区域，还考虑整图纹理信息。
图像修补是病态问题，解是不确定的：
- 领域复杂性：需修补区域随应用而不相同。
- 图像复杂性：性质在不同尺度表现不同。
- 模式复杂性：要考虑视觉上有意义的模式。
7.4.2 全变分模型⚓
用于去除划痕或尺寸较小靶区域的修复技术。
基于偏微分方程或变分模型，两者可以借助变分原理相互等价推出（优化技术）。
通过对靶区域进行逐个像素的扩散来达到修复图像的目的。
沿着等光强线（相等灰度值的线）由源区域向靶区域延伸扩散，扩散时可借助全变分模型(TV)来恢复图像中的缺失信息。
优点是可以很好地保持图像中的线性结构，缺点是不一定能保持图像细节。
7.5 区域填充⚓
修补大尺度区域时，修复方法将缺失区域周围的信息向中心扩散，对尺度较大的缺失区域，扩散会造成一定的模糊，且模糊程度会随缺失区域的尺度增加而增加。修复方法没有考虑缺失区域内部的纹理特性，将缺失区域周围的纹理特性直接移入缺失区域内。由于对尺度比较大的缺失区域内外纹理特性可能有较大的差别，导致修复结果不很理想。
解决思路/方案：
(1) 将图像分解为结构部分和纹理部分，对结构性强的部分用扩散方法进行插补，而对纹理明显的部分则借助纹理合成的技术进行填充。
这是是一种混合的方法，扩散的方法借助了结构信息，但要完全用纹理合成来填补大面积的靶区域仍有一定风险和难度。
(2) 在图像未退化部分选择一些样本块，先用这些样本块来替代拟填充区域边界处的图像块（这些块的未退化部分与所选样本块有接近的特性），并类似地逐步向拟填充区域内部递进填充。
这种方法常称为基于样本的图像填充方法。这类方法直接用源区域中的信息（包括纹理信息）来填补靶区域。
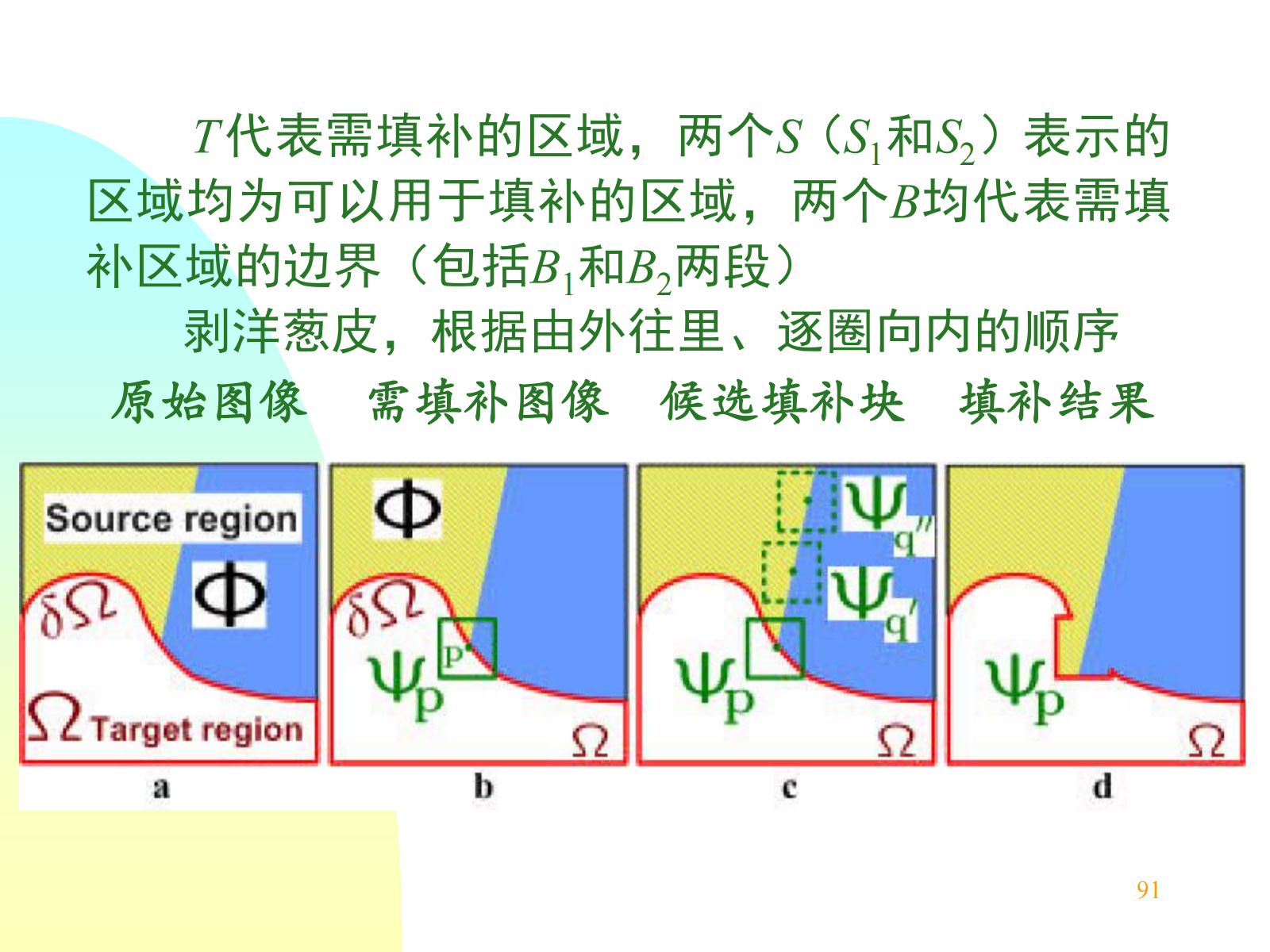
7.5.1 基于样本的方法⚓
使用保持原状的空间区域去估计和填充待修补部分中缺失的信息。
(1) 在需要填充区域的轮廓上计算权重，选择权重最大的轮廓点作为待填充点。
(2) 在该点周围领域取一个一定大小的 patch 块，在图像其他区域内找该 patch 块的最近邻 patch。
(3) 将最近邻 patch 块对应到需要填充区域的部分复制到等待填充的区域，再重复上述步骤，直至所有点都填充完毕。
图像的填充顺序对于该算法至关重要。
基于样本的算法的共有缺陷：无法应对没有合适填充样例的图片；无法保证最终填充图像的整体效果。
7.5.2 结合稀疏表达的方法⚓
