8 z 变换、离散时间系统的 z 域分析¶
8.1 z 变换的定义¶
抽样信号 \(x(nT)\) 的 Laplace 变换:
单边 z 变换,由 Laplace 变换引入:
定义 \(z = e^{sT}\) ,有:
取 \(T=1\) 得到:
单边 z 变换也可以由洛朗级数引出。若 \(f(z)\) 在去掉圆心的圆盘 \(D: 0 < |z - z_0| < R\) 内确定并且解析,那么 \(z_0\) 称为 \(f(z)\) 的孤立奇点。在 \(D\) 内,\(f(z)\) 有洛朗级数:
其中:
\(C_\rho\) 是圆 \(|z - z_0| = \rho\) ,将 \(z\) 变换定义为复变量 \(z^{-1}\) 的幂级数
即 \(z_0 = 0\) 的洛朗级数。
单边 \(z\) 变换:
双边 \(z\) 变换:
自变量 \(z\in\mathbb{C}\) 为复变量。因果信号的单边与双边 \(z\) 变换结果相同。
查表:附录5 序列的 z 变换表。
8.2 z 变换的收敛域(ROC)¶
不同序列的 \(z\) 变换可能相同,如 \(a^nu(n),\;a^nu(-n-1)\) .
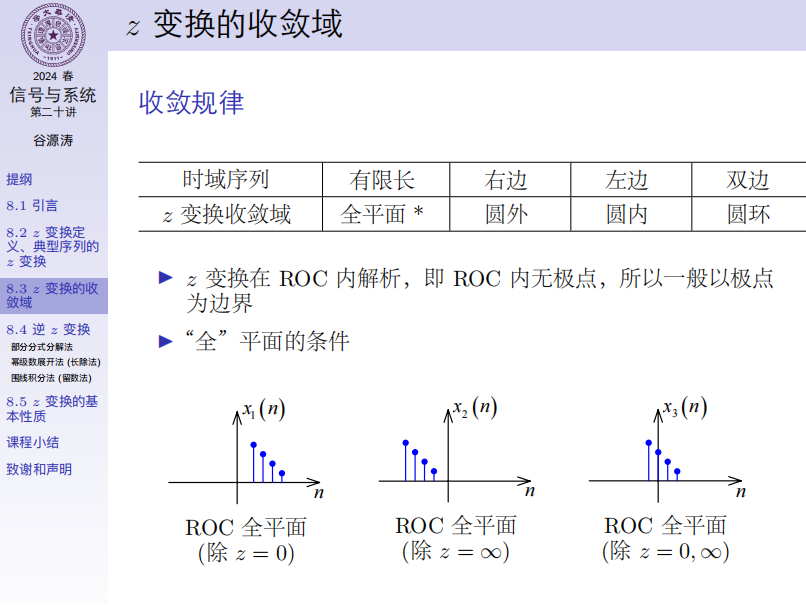
每一个 \(z\) 变换式要标注 ROC。在 ROC 内 \(z\) 变换函数解析,因此 ROC 内不会有极点。有理函数以 ROC 以极点为边界。
收敛的充分条件是绝对可和: \(\displaystyle\sum_{n=-\infty}^{\infty} x(n)z^{-n}<\infty\) ,回忆级数收敛的判定方法——比值判定和根植判定:
\(\rho<1\) 收敛, \(\rho>1\) 发散, \(\rho=1\) 不确定。
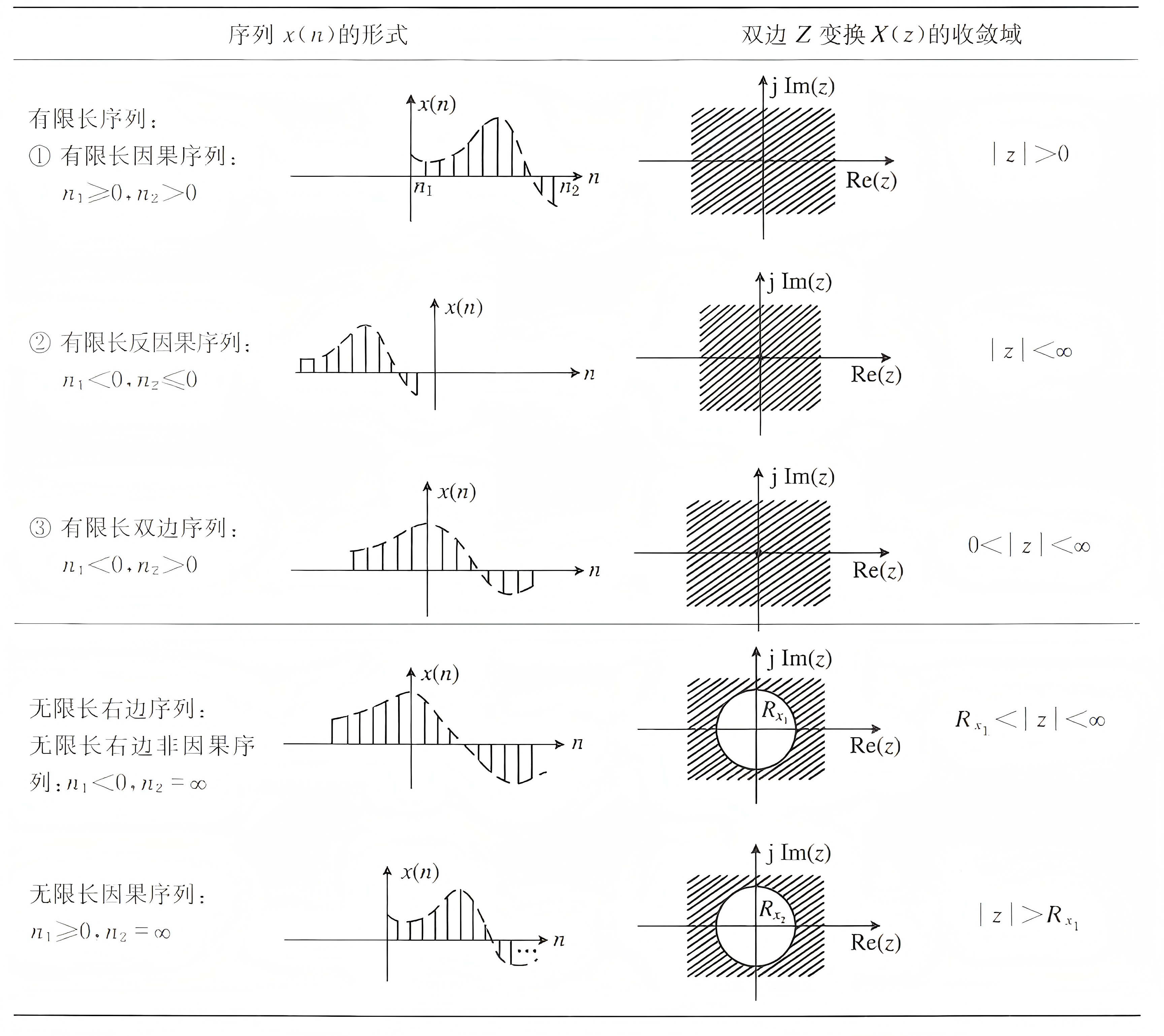
(课本 P53,表8-1)对于双边 \(z\) 变换,序列的 ROC:
-
有限长序列:几乎为整个平面。
(1)原点左右均有, \(0<|z|<\infty\) .
(2)原点及其右边, \(0<|z|\) .
(3)原点及其左边, \(|z|<\infty\) .
有限长序列,求和范围里有 \(n>0\) 的项,ZT 中会含有 \(\dfrac{1}{z}\) ,因此 ROC 不包含 \(z=0\) .
求和范围里有 \(n<0\) 的项,ZT 中会含有 \(z\) 的乘方,因此 ROC 不包含 \(z=\infty\) .
-
右边序列:圆外( \(z\) 要足够大,抑制序列的增长)。
(1)包含原点,有原点左边的部分(非因果), \(R_{x1}<|z|<\infty\) .
(2)原点及其右边(因果), \(R_{x1}<|z|\) .
-
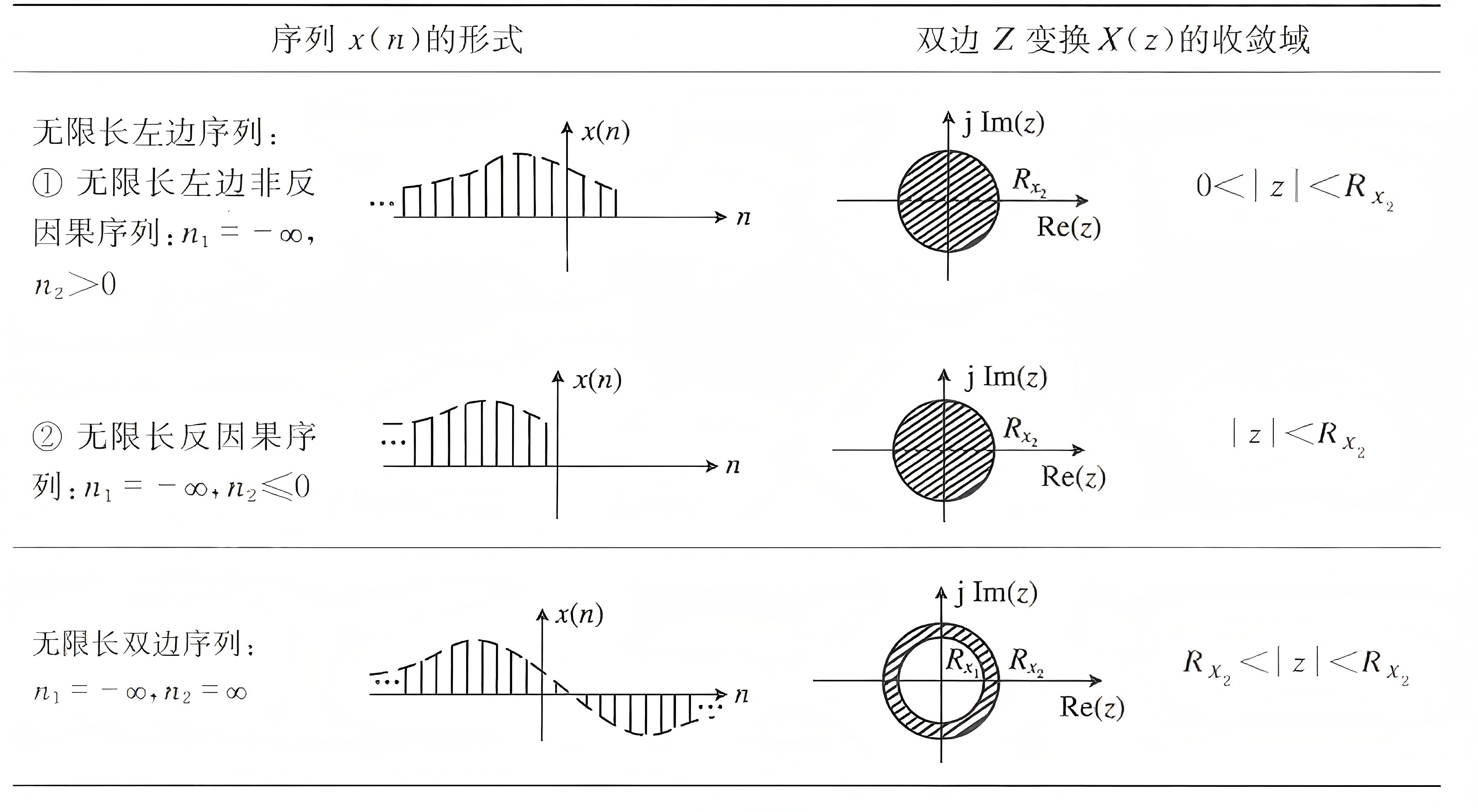
左边序列:圆内( \(\dfrac{1}{z}\) 要足够大,抑制序列的增长)。
(1)包含原点,有原点右边的部分, \(0<|z|<R_{x2}\) .
(2)原点及其左边, \(z<R_{x2}\) .
-
双边序列:圆环, \(R_{x1}<|z|<R_{x2}\) .
8.3 逆 z 变换¶
定义式(可以救急用):
积分路径 \(C\) 是包含 \(X(z)z^{n-1}\) 所有极点的逆时针闭合曲线,通常选择 \(z\) 平面收敛域内以原点为中心的圆。
围线积分法(留数法):一般不用。
幂级数展开法(长除法):一般不用。
部分分式展开法:常用,简单。
因果序列的 \(z\) 变换 ROC 在圆外,为保证在无穷远处收敛,分母多项式阶次应不小于分子多项式。
大多数情况 \(X(z)\) 下只有一阶极点,将 \(\dfrac{X(z)}{z}\) 展开为 \(\dfrac{z}{z-z_m}\) 的形式:
如果有高阶极点:
Tip
部分分式展开要多练习。
查表:课本P61,表8-2 逆 \(z\) 变换表。
8.4 z 变换的性质¶
查表:课本 P74,表8-5 \(z\) 变换的主要性质。
(1)线性。
(2)时移特性。
对于双边 \(z\) 变换,位移只会使 \(z\) 变换在 \(z=0\) 或 \(z=\infty\) 的零极点情况发生变化。若 \(x(n)\) 为双边序列,ROC 为圆环,位移不会改变 ROC。
对于单边 \(z\) 变换,分左移和右移两情况。左移需要把将要移到左边的那部分减掉,右移需要把原来“藏”在左边的部分加上来。对因果序列也有特殊讨论。
(3)序列线性加权, \(z\) 域微分。
(4)序列指数加权, \(z\) 域尺度变换。
(5)初值定理。
(6)终值定理。要求 \(n\to\infty\) 的时候序列 \(x(n)\) 收敛,也就是 \(X(z)\) 的极点在单位圆内,或者 \(z=+1\) 点处的一阶极点。
(7)时域卷积, \(z\) 域相乘。一般情况下新序列 ROC 为二者 ROC 的重叠部分,但是有可能 ROC 边缘发生零极点相消,使 ROC 扩大。
(8)序列相乘, \(z\) 域卷积。
(9)尺度变换性质,这个在郑君里教材《信号与系统》和课件中均未提及。但是2020年期末考试中出过这样一道题: \(x(2n+1)\) 的双边 \(z\) 变换。
我们可以直接推导:
8.5 z 变换与 Laplace 变换的关系¶
ZT 和 LT 表达式的对应:可以直接由 LT 表达式写出 ZT 表达式:
用这个可以推导出正弦序列的 \(z\) 变换。
在某些点发生跳变似乎要单独讨论......但这似乎不重要。
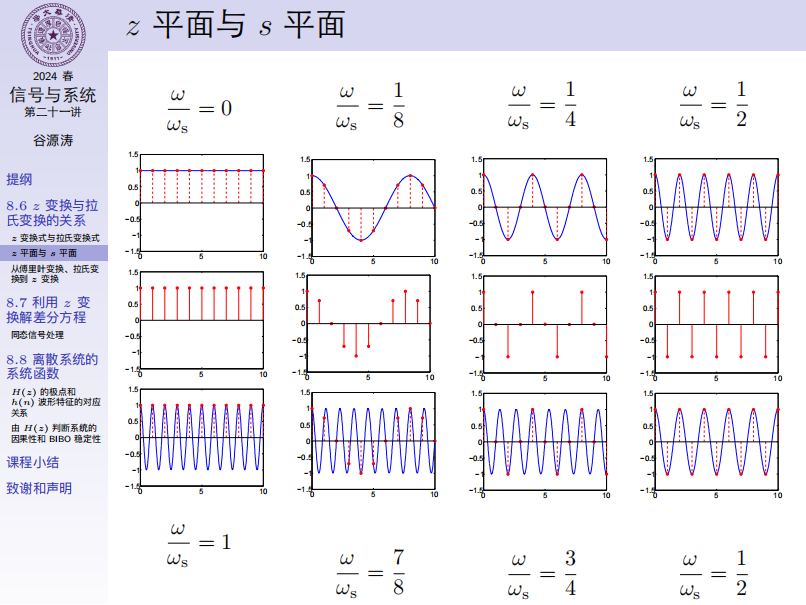
\(T\) 为序列的时间间隔,则 \(z\) 平面与 \(s\) 平面的映射关系为:
\(s\) 平面的虚轴对应 \(z\) 平面单位圆,右半平面映射到单位圆外,左半平面映射到单位圆内。
\(s\) 平面的实轴对应 \(z\) 平面正实轴, \(s\) 平面平行于实轴的直线对应 \(z\) 平面始于原点的射线,且通过 \(\mathrm{j}\dfrac{k\omega_s}{2}\) 的平行于实轴的直线对应 \(z\) 平面的负实轴。
\(s\) 平面沿虚轴移动, \(z\) 平面上绕单位圆周期旋转。每平移 \(\omega_s\) ,沿单位圆绕一圈,因此一个 \(z\) 值对应多个 \(s\) 值。
查表:课本 P80,表8-7 常用信号的 LT 与 ZT。
8.6 利用 z 变换解差分方程¶
幂级数展开(长除法)、卷积定理(分解为相乘形式,在时域卷积)、留数法(太麻烦,实际中不用)。
8.7 离散系统的系统函数¶
单位样值响应与系统函数¶
LTI 系统,单位样值响应 \(h(n)\) 与系统函数 \(H(z)\) 是一对 \(z\) 变换对:
可以根据系统函数的零极点分布确定单位样值响应。
展开为部分分式:
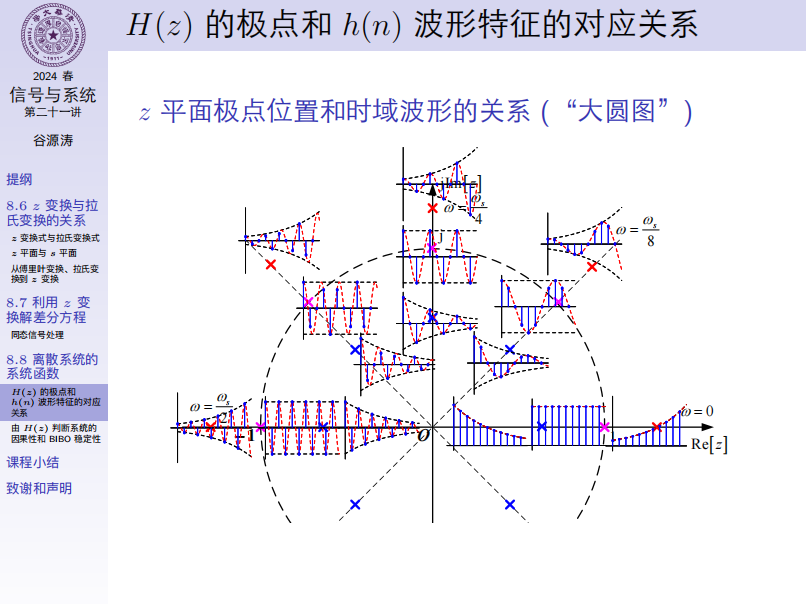
极点 \(p_k\) 一般以共轭复数形式出现。可见 \(h(n)\) 的特性取决于 \(H(z)\) 的极点,幅度由系数 \(A_k\) 决定,而系数 \(A_k\) 由 \(H(z)\) 的零点分布有关。与 LT 类似, \(H(z)\) 的极点决定 \(h(n)\) 的波形特征,零点只影响 \(h(n)\) 的幅度和相位。
“大圆图”,课本 P86。
z 域考察离散时间系统的因果性和稳定性¶
系统稳定的充要条件是单位样值响应 \(h(n)\) 绝对可和:
因此稳定系统的系统函数收敛域必然包含单位圆,这是一个必要条件。
系统因果的条件为 \(h(n)=h(n)u(n)\) ,即 \(z\) 变换的收敛域为圆外且包含无穷远点。
综上,因果稳定系统的收敛域应该同时满足:
这也限制了所有极点都在单位圆内。
8.8 离散时间傅里叶变换(DTFT)¶
离散时间傅里叶变换 DTFT(Discrete Time Fourier Transform)定义为:单位圆上的 \(z\) 变换。注意,DTFT 与离散傅里叶变换 DFT 完全不同,DFT 是对 DTFT 的有限均匀采样,它的时域和频域序列都是离散的、有限长的,适用于实际的数字系统存储和运算,有关 DFT 的学习将在《数字信号处理》进行。
定义和收敛条件¶
又有:
称 \(X(e^{\mathrm{j}\omega})\) 为序列 \(x(n)\) 的频谱, \(|X(e^{\mathrm{j}\omega})|\) 为幅度谱, \(\varphi(\omega)\) 为相位谱。
由于 \(\omega\) 沿单位圆旋转, \(X(e^{\mathrm{j}\omega})\) 是以 \(2\pi\) 为周期的周期函数。
时域是离散的,频域是连续的。
DTFT 存在的充分条件:序列 \(x(n)\) 绝对可和。其存在的必要条件至今未找到(FT 也如此)。
基本性质¶
- 线性。
- 时域位移。
- 频域位移。
- 线性加权,频域微分。
- 反褶。
- 奇偶虚实性,参照 FT。
- 时域卷积,频域卷积。
- 帕塞瓦尔定理:能量守恒。
- 共轭: \(x^*(n)\iff X^*(e^{-\mathrm{j}\omega})\) . 因此对于实函数: \(X(e^{\mathrm{j}\omega})=X^*(e^{-\mathrm{j}\omega})\) .
8.9 离散时间系统的频率响应¶
由系统函数 \(H(z)\) 到频率响应 \(H(e^{\mathrm{j}\omega})\) ,回忆连续时间系统的系统函数 \(H(s)\) 到频率响应 \(H(\mathrm{j}\omega)\) .
连续时间系统的特征函数是 \(e^{st}=e^{\mathrm{j}\omega t}\) ,输入信号为 \(e^{\mathrm{j}\omega t}\) 的情况下输出信号为:
离散时间系统的频响函数为:
离散时间系统特征函数为: \(z^{n}=e^{\mathrm{j}\omega n}\) ,对复指数序列/正弦序列激励的稳态响应为:
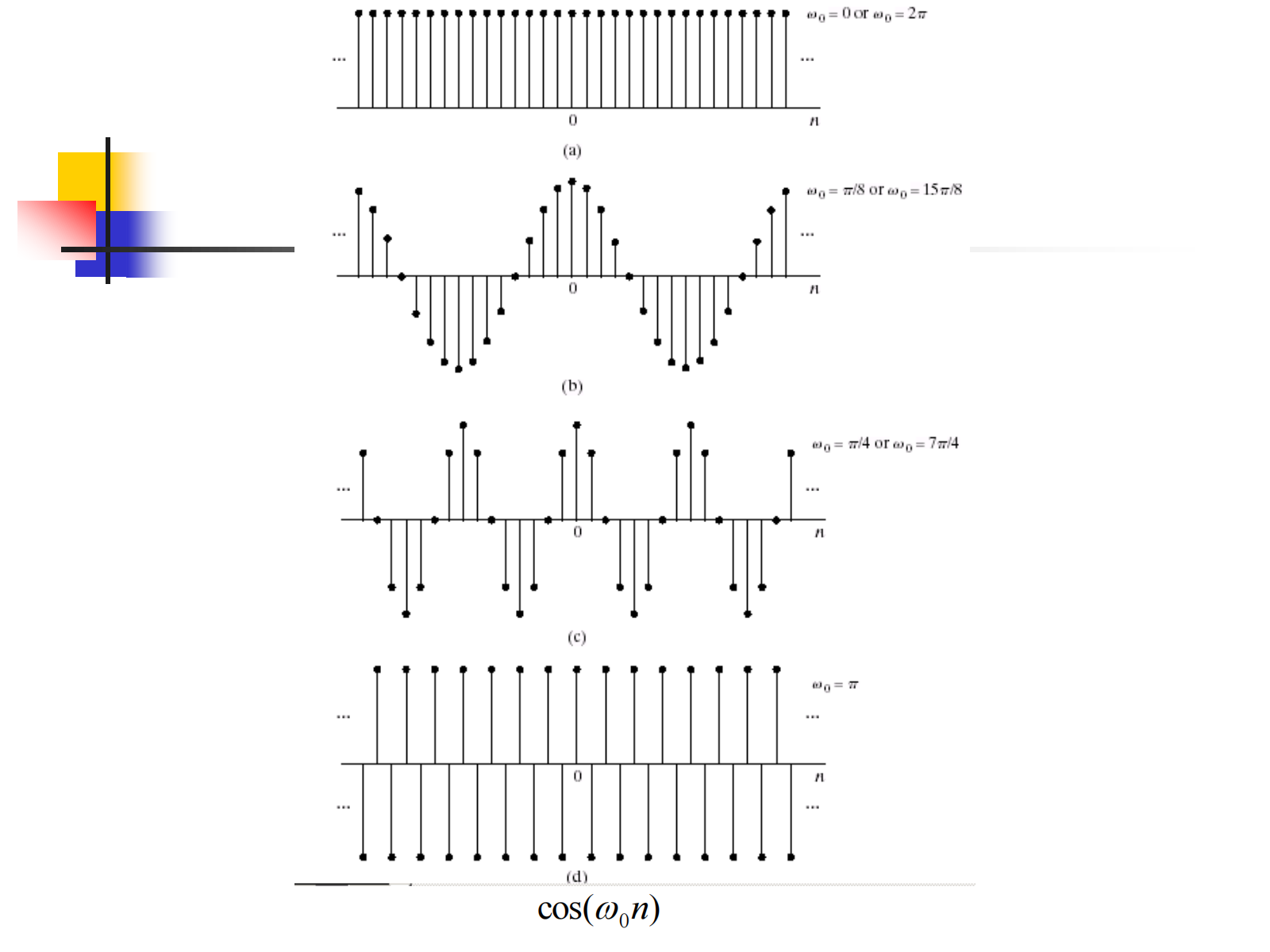
离散信号中频率 \(\omega\) 和 \(\omega+2k\pi\) 是不可区分的: \(\sin((\omega+2k\pi)n+\varphi)=\sin(\omega n+\varphi)\) .
频率响应 \(H(e^{\mathrm{j}\omega})\) 和单位样值响应 \(h(n)\) 是一对 Fourier 变换对。
频率响应 \(H(e^{\mathrm{j}\omega})\) 为周期函数,周期为 \(\omega_s=\dfrac{2\pi}{T}\) .
判定频率响应特性,只需关注一个周期 \((0,\omega_s)\) 内的情况。
如果为实系数, \(|H(e^{\mathrm{j}\omega})|\) 为偶函数, \(\varphi(\omega)\) 为奇函数,也只需要关注半个周期 \(\left(0,\dfrac{\omega_s}{2}\right)\) 内的情况。 \(0\) 和 \(\omega_s\) 是最低数字频率, \(\dfrac{\omega_s}{2}\) 是最高数字频率,以此来判断低通/高通/带通/带阻/全通的系统特性。
频率响应的几何确定法:
画图,长度乘除决定幅度特性,夹角加减决定相位特性。
幅度响应靠近极点处出现峰点,靠近零点处出现谷点。 \(z=0\) 处的零极点只影响相位响应,不影响幅度响应。
8.10 z 变换应用实例¶
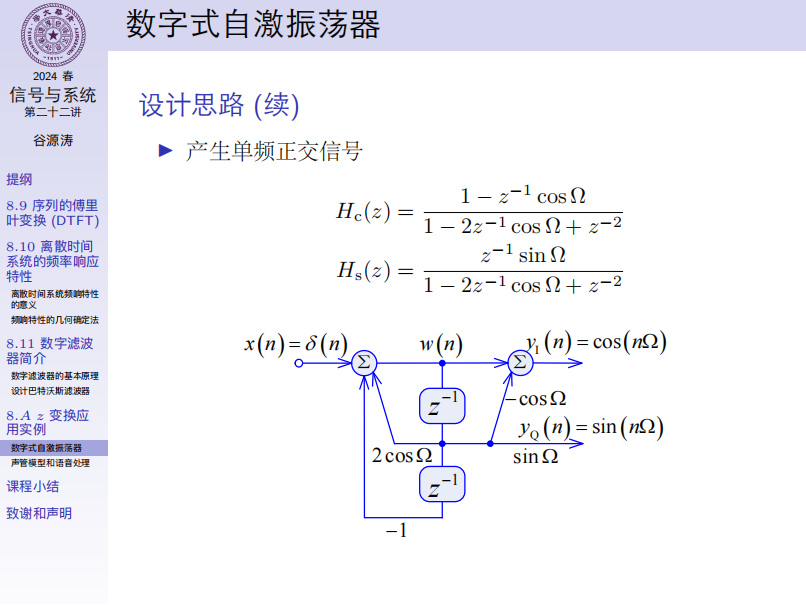
数字式自激振荡器:
结构上改进:使用中间信号 \(W(z)\) 实现结构复用,系统可同时产生 \(\sin(\cdot)\) 和 \(\cos(\cdot)\) 信号。
数字滤波器:
原理:输入的连续信号 \(x(t)\) 频带受限 \(-\omega_m\sim\omega_m\) ,抽样间隔满足奈奎斯特抽样频率 \(\omega_s=\dfrac{2\pi}{T}\geqslant2\omega_m\) .
冲激不变法设计数字滤波器(低通):
根据 ZT 和 LT 的关系,由模拟域到数字域,直接改写式子:
要求频率响应 \(H(\mathrm{j}\omega)\) 在 \(0\sim \dfrac{\omega_s}{2}\) 内衰减足够快。
优点:简单,便于与模拟滤波器直接对应。
缺点: \(s\) 与 \(z\) 的多值对应关系可能引起混叠,且只能设计低通滤波器,不能用于设计高通和带阻滤波器。