第三章空域图像增强⚓

3.1 图像增强概述⚓

图像增强：目的是对图像进行加工处理，以得到对于人、机器视觉和识别应用而言，更好、更有用的图像。

点操作：对单点像素操作，与邻域无关。模板操作的特例。

模板操作：对图像某个区域操作。

3.2 空间变换增强⚓

3.2.1 图像间运算⚓

图像间算术运算：加（可平均消除噪声）、减（可凸显差异，如运动物体检测）、乘、除。

图像间逻辑运算：与（mask操作）、或、非、异或。

补充知识：

色温是表示光线中包含颜色成分的一个计量单位，以温度的度量单位来记录颜色的程度，可以简单理解为颜色的温度。当黑体加热到一定的温度，黑体发出的光所含的光谱成分，就称为这一温度下的色温，计量单位为“K”（开尔文）。在摄影中，某一光源发出的光，与某一温度下黑体发出的光所含的光谱成分相同，就称为某K色温。

白平衡：白色的平衡，由于人眼的适应性，在不同色温下，都能准确判断出白色，但是相机在不同色温的光源下，会出现图像偏色，与人眼看到的颜色不一致，因此需要进行白平衡处理。

白平衡算法——灰度世界算法：

以灰度世界假设为基础，认为对于一幅有着大量色彩变化的图像, RGB 三个分量的平均值趋于同一个灰度 K。

确定灰度 K：取固定值128或 RGB 三通道的平均值。
计算各通道增益，即 K 与通道均值之比。
根据增益调整 RGB 分量。

白平衡算法——完美反射算法：

假设图像世界中最亮的白点是一个镜面，能完美反射光照。基于白点，将三通道的数值进行适当地调整，以达到白平衡效果。

计算每个像素的 RGB 通道之和，按大小计算出其前10%或其他比例的白色参考点的阈值 T。
计算图像三通道数值和大于 T 的点（即亮区）的各通道均值。
计算各通道增益，即通道最大值(如255)与亮区通道均值之比，然后各个通道乘以对应增益。

3.2.2 图像灰度映射⚓

灰度映射函数 \(t=E_H(s)\)。

基本灰度变换：图像求反，增强对比度，动态范围调整（压缩），灰度切分，伽马校正。

图像求反：灰度值反转 \(t=(L-1)-s\)，黑变白，白变黑。

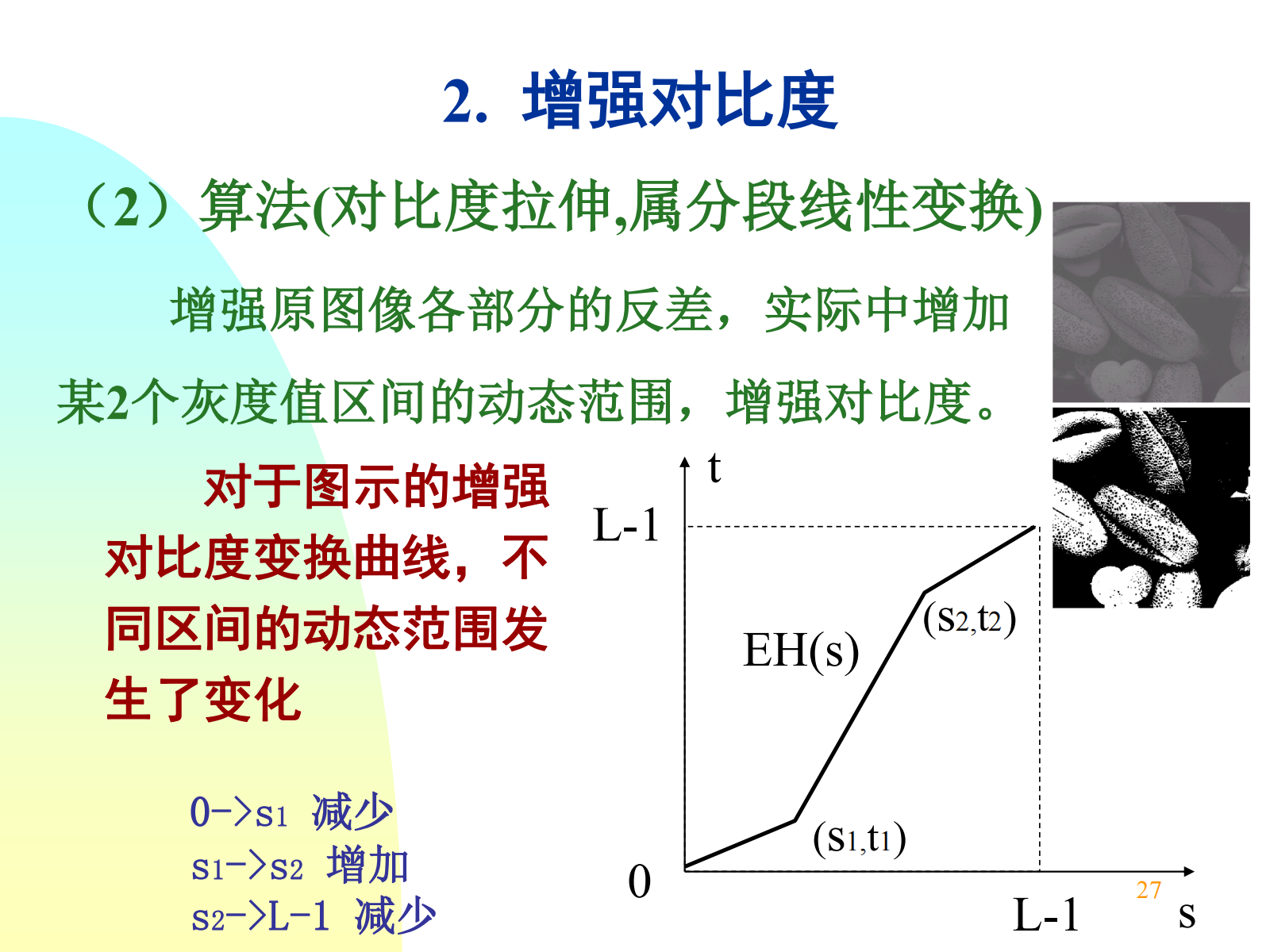
增强对比度：分段拉伸函数。

动态范围调整(压缩)：调整灰度变化的动态范围，低灰度范围的值扩展，高灰度范围的值压缩，使图像分布均匀。常用对数变换 \(t=c\cdot\log(1+s)\) ，上凸函数。

动态范围压缩：将灰度范围减小，压缩原图灰度值。有时图像的动态范围太大，超出显示设备允许动态范围，导致丢失细节。

动态范围

人眼适应光强度级别范围很宽，从夜视阈值到强闪光，约有 \(10^10\) 量级，但是人眼不能同时在一个范围内工作。昼视觉范围 \(10^6\) 比总适应范围要小。

同一个场景里往往会同时出现很多不同亮度的部分，我们把这个场景的最大亮度与最小亮度的跨度称作动态范围，最大亮度和最小亮度的比叫（静态）对比度。

人眼鉴别能力实验：不同背景光强度下的亮度鉴别能力。对给定背景亮度有50%的机会回答 yes 时，\(\Delta I_c\) 为增量，\(\Delta I_c/I\) 为韦伯比。韦伯比小表示可以区分强度小的变化，代表较好的亮度区分，韦伯比大代表亮度区分能力差。实验表明，当背景亮度低时，韦伯比较大，亮度鉴别能力低。

人眼的感觉亮度问题：感觉亮度不是简单的强度函数——马赫带效应，当人眼观察一系列亮度逐渐变化的条带时，会在每个亮度交界处看到非真实存在的亮或暗边缘。

Question

我个人认为增强对比度和动态范围调整的主要区别：增强对比度是为了增强图像中不同灰度之间的感知差异，可以在原区间内操作，也可以通过扩展灰度区间实现；动态范围调整是为了让图像占满更多或全部灰度范围（通常会改变灰度范围），从而避免灰度压缩，不一定关注视觉对比效果。

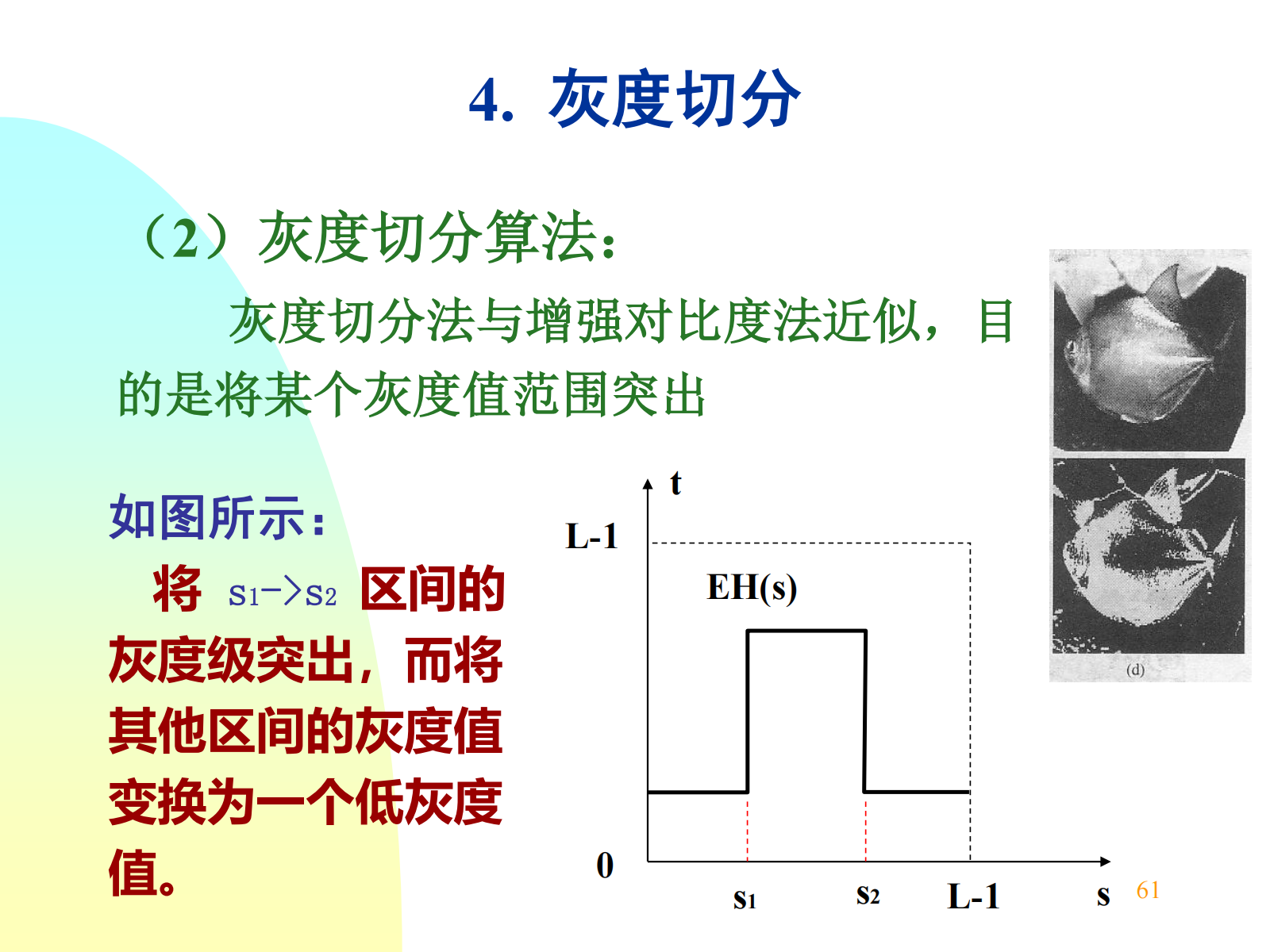
灰度切分：突出某一范围的灰度，将 \(s_1 \to s_2\) 区间的灰度级突出，使得代表该部分的物体明显显示，如裂纹的增强显示，而将其他区间的灰度值变换为一个低灰度值。

伽马校正：\(t=Cs^{\gamma}\)，\(\gamma<1\) 提高灰度级，在正比函数上方，使图像变亮。\(\gamma>1\) 降低灰度级，在正比函数下方，使图像变暗。

3.2.3 直方图变换⚓

Abstract

以概率论为基础，通过改变图像的直方图，改变图像中像素的灰度，实现图像增强。也常称直方图修正。

图像的灰度统计直方图，\(p_s(s_k)=\dfrac{n_k}{n}\) 代表某一灰度出现的概率估计。

直方图表示一幅图像的整体灰度分布，不包含空间位置信息的灰度分布。因此图像与直方图的关系是多对一。对一张图像进行平移、旋转、尺度等变换，不改变直方图。

直方图均衡化：

变换原始图像的直方图为均匀分布，使灰度层次丰富；使像素灰度值的动态范围最大，增强图像整体对比度。

直方图均衡化以累积分布函数(CDF)变换为基础，将原始图像的直方图，由不均匀分布变换为均匀分布。实际中并不会达到理想的均匀分布，而是更加接近于均匀分布。

变换函数应满足：在 \(0\leqslant s \leqslant L-1\) 区间内单值单增，且值域动态范围 \([0, L-1]\) 不变。这样可以保证原图像灰度级在变换后仍保持从黑到白的排列顺序，单值保证反变换存在。

累积直方图：\(t_k=EH(s_k)=\displaystyle\sum_{i=0}^{k}\dfrac{n_i}{n}\)。由原图像从0至第 k 个灰度级的概率密度函数的累积和，作为新图像的第 k 级灰度的灰度值。相当于将概率密度函数积分为分布函数。

步骤：

原图像统计直方图，计算出归一化直方图，再得到累计直方图。
区间转换，乘上“灰度级最大值-1”并四舍五入，如最常见的乘 \(256-1=255\) ，得到原像素和均衡化后像素的映射关系。

均衡化的优点是：可以自动地增强图像全体的对比度。缺点是，只能产生近似均匀的直方图，并且是全局均衡化直方图，增强效果不易控制。

直方图规定化：

核心思想是正确选择规定化的函数，使输出图像具有规定的概率密度函数，实现有选择地增强某个范围灰度值。

原始直方图的灰度级概率密度函数 \(p_s(s)\)，希望得到规定直方图的灰度级概率密度函数 \(p_u(u)\)，步骤：

对原始直方图进行灰度均衡化：\(t_k={EH}_s(s_k)=\displaystyle\sum_{i=0}^k p_s(s_i),k=0,\dots M-1\)。
计算能使规定直方图均衡化的变换：\(v_k={EH}_u(u_k)=\displaystyle\sum_{i=0}^k p_u(u_i),k=0,\dots N-1,N\leqslant M\)。
求规定直方图的反变换函数 \(u={EH}_u^{-1}(v)\)。
原始直方图中所得到灰度级 \(t\) 代入反变换函数：\(u={EH}_u^{-1}(t)={EH}_u^{-1}[{EH}_s(s)]\)。需要找出 \(t\) 与 \(v\) 的近似值，两者近似相等时的 \(s,u\) 对应，完成从 \(s\to u\) 的变换。

规定化的结果与预期值一般存在误差，并不能完全实现目标直方图，是因为灰度值的离散化和多次近似。

3.3 空间滤波增强⚓

3.3.1 像素间联系⚓

欧氏距离 \(D_E(p,q)=\sqrt{(x-s)^2+(y-t)^2}\) 。

曼哈顿距离/城区距离 \(D_M(p,q)=|x-s|+|y-t|\) 。

棋盘距离 \(D_C(p,q)=\max{(|x-s|,|y-t|)}\) 。

像素的邻接：有接触，仅考虑空间关系。

4-邻域 \(N_4(p)\)：曼哈顿距离为1，边接触，类型为 4-邻接。

8-邻域 \(N_8(p)\)：棋盘距离为1，边接触+顶点接触，类型为 8-邻接。

仅有点接触的4个像素点组成 D-邻域 \(N_D(p)\)，故 \(N_8(p)=N_D(p)+N_4(p)\)。

通路：由一系列依次邻接的像素组成。通路中相邻两个像素仅有邻接关系。由此定义出 4-通路，8-通路。

像素的连接：考虑空间和属性关系，有接触且灰度值相似（相等，或者在同一个集合中取值）。

4-连接：2两个像素相似且 \(r\in N_4(p)\)。

8-连接：2两个像素相似且 \(r\in N_8(p)\)。

连通：由一系列依次连接的像素组成。连通中相邻两个像素有连接关系。由此定义出 4-连通，8-连通。

连通是连接的推广，连接是连通的特例。

子集：图象中的（部分）像素的集合。

连通组元：在一个图像子集中与同一个像素相连通的所有像素构成该图像子集中的一个连通组元。（类比离散数学中的连通集）连通组元内的2个像素互相连通，不同连通组元中的各个像素互不连通。

连通集：如果子集 S 中只有一个连通组元，即 S 中所有像素都互相连通，则称 S 是一个连通集。

区域：一个连通集合称为图像的一个区域。一般来说，区域是最大的连通集，是图像中一个语义上完整的“对象”。

边界（轮廓）：是区域的一个子集，它将该区域与其他区域分离开，组成区域的边界像素本身属于该区域而在其邻域中有不属于该区域的像素，可理解去与边缘出的像素子集。

像素集合的邻接（图像子集的邻接）：2个图像子集 S,T 中的若干像素相邻接，则 S 和 T 邻接。有 4-邻接、8-邻接类型。

像素集合的连通（图像子集的连通）：2个图像子集 S,T 中的若干像素相连接，则 S 和 T 连接。有 4-连通、8-连通类型。

3.3.2 模板运算⚓

模板卷积步骤：

(1) 模板在图中滑动，中心与像素重合。(2) 模板系数与对应像素值相乘。(3) 所有乘积相加。(4) 将和赋予与模板中心对应的像素。

当模板超出图像边界时，可以忽略边界之外的部分，也可以进行填充 padding。

空域滤波增强有：线性/非线性，平滑/锐化。

线性滤波器，是对观察结果的线性组合，即输出是输入的叠加。线性方法通常可将复杂的运算进行分解，计算比较方便，容易并行实现。

非线性滤波器，是对观察结果的逻辑组合，滤波效果较好，但较为复杂。主要定义为基于集合的，基于形状的（形态学），基于排序的（中值滤波）3种。

常见噪声：高斯噪声，脉冲噪声（椒盐噪声），瑞利噪声，均匀分布噪声，伽马噪声，指数分布噪声。

椒盐噪声

椒盐噪声也称为脉冲噪声，表现为随机的黑点和白点，黑色为胡椒，白色为盐。若脉冲有一种，脉冲噪声称为单极脉冲，若脉冲有两种，脉冲噪声称为双极脉冲/椒盐噪声。

椒盐噪声的成因可能是影像讯号受到突如其来的强烈干扰而产生、类比数位转换器或位元传输错误等。例如失效的感应器导致像素值为最小值，饱和的感应器导致像素值为最大值。

中值滤波对消除椒盐噪声效果最好，因为不会像使用均值滤波器那样发生孤立噪声点对均值的影响。

线性平滑滤波——均值滤波器：

邻域平均。
加权平均。
高斯平均。
边缘保持平滑，取中心像素的8个不同邻域，对每个邻域都统计其像素的灰度方差，并将灰度方差最小（方差小的邻域中像素灰度级的变化小，包含边缘的概率也小）的那个邻域中的像素均值赋给中心像素。用于模糊处理和减小噪声，提取大目标时消除细节、缝隙。属于低通滤波器。

非线性平滑滤波——中值滤波器：依靠 NxN 的模板对图像进行中值平滑处理，利用区域的中值进行平滑。让与周围像素灰度值相差较大的像素改取与周围灰度值接近的值。消除孤立噪声能力强，因为不是简单地取均值，产生模糊较少，保持细节。

锐化滤波器：基于微分。

一阶导数可以用于检测图像中的一个点是否是边缘的点。二阶导数的符号可以用于判断一个边缘像素是在边缘亮的一边还是暗的一边。一阶微分算子和二阶微分算子均可以作为图像边缘检测算子。

基于梯度的锐化滤波：梯度算子（一阶微分），X 和 Y 方向两种差分模板。

\[ \begin{bmatrix} -1 & 0 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1 \\ \end{bmatrix} \text{and} \begin{bmatrix} 1 & 1 & 1 \\ 0 & 0 & 0 \\ -1 & -1 & -1 \\ \end{bmatrix} \]

\[ \begin{bmatrix} z1 & z2 & z3 \\ z4 & z5 & z6 \\ z7 & z8 & z9 \\ \end{bmatrix} \]

实际滤波中只取梯度矢量的模： \(|\nabla f|=\sqrt{G_x^2+G_y^2}\approx |G_x|+|G_y|=|z8-z5|+|z6-z5|\) 。取模操作导致梯度算子是非线性的。

Robert 交叉差分 \(|\nabla f| \approx |z9-z5|+|z8-z6|\) 。

拉普拉斯算子：一种线性锐化滤波器。对噪声敏感，但可用于孤立点检测。

基于二阶微分：拉普拉斯算子，4-邻域或8-邻域（系数之和均为0）：

\[ \begin{bmatrix} 0 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 0 \end{bmatrix} \text{or} \begin{bmatrix} -1 & -1 & -1 \\ -1 & 8 & -1 \\ -1 & -1 & -1 \end{bmatrix} \]

拉普拉斯算子可增强图像中的灰度不连续边缘，减弱灰度值缓慢变化区域的对比度，将结果叠加到原始图像上，得到锐化后的图像。

高频提升滤波：原图像叠加微分结果，等价于原图像减去积分结果 \(h_b(x,y)=A*f(x,y)-g(x,y)=(A-1)*f(x,y)+h(x,y)\) 。

最大-最小锐化变换：一种非线性锐化滤波。

最大值滤波和最小值滤波结合，将一个模板覆盖区域里的中心像素值与该区域里的最大值和最小值比较，将中心像素值用与其较接近的极值替换。

线性和非线性混合滤波：将线性滤波运算和中值滤波运算混合串联起来，先对较大的区域进行计算量较小的线性滤波操作，然后再计算线性滤波输出的中值，作为混合滤波的最终输出。

双边滤波：

邻域内加权平均，但同时考虑像素的空间邻近度和像素值相似度，不会像普通高斯滤波一样模糊边缘。在高斯滤波的基础上，邻域内灰度值越接近中心点灰度值的点的权重更大，灰度值相差大的点权重越小。最终权重大小由空间域高斯核函数和值域高斯核函数共同确定。

引导滤波，一种双输入（多模态）的保边滤波方法。

输入图为 p，引导图为 I，输出图为 q，其中引导图可以是其他图像也可以是输入图像本身，算法步骤为：

设定一定步长和大小的滑动窗，对每个位置的滑动窗 \(\omega_k\) 计算期望，方差，协方差：\(\mathbb{E}[p],\mathbb{E}[I],\text{Var}(I),\text{Cov}(p,I)\)
对每个位置的期望，方差，协方差计算滤波参数 \(a_k，b_k\) ，得到 ak 图，bk 图：\(a_k=\dfrac{\text{Cov}(p,I)}{\text{Var}(I)+\varepsilon},b_k=\mathbb{E}[p]-a_k \mathbb{E}[I]\) 。
再用滑动窗对引导图 I 进行滤波，得到输出图：\(q_i=\dfrac{1}{|\omega|}\displaystyle\sum_{k:i\in \omega_k}(a_kI_i+b_k)\) 求和过程中只有 \(I_i\) 改变，对于同一个窗口 \(a_k,b_k\) 为定值。

Note

双边滤波和引导滤波都是保边滤波器。

保边滤波器(Edge-Preserving Filters)是一类在平滑图像的同时能够保留边缘信息的图像处理技术，目的是减少图像噪声的同时保持边缘清晰，而传统平滑滤波器（如均值滤波、高斯滤波、中值滤波等）属于各向同性滤波，噪声和图像边缘信息会被同等处理。

3.4 局部增强⚓

局部增强：对图像某些局部区域的细节进行增强。多了一个选择局部区域的步骤。

直方图变换局部增强：先将图像分成一系列小区域（子图像），对各子图像分别进行直方图变换。

Example

自适应直方图均衡化(AHE)，计算图像局部直方图，重新分布来改变图像对比度，但可能过度放大相同区域的噪声。对比度限制自适应直方图均衡化(CLAHE)通过限制直方图的幅度进一步改善。在我的《数字图像处理》大作业中，人脸图像预处理使用到了 CLAHE 算法，详见仓库 DerrickMarcus/digital-image-project。

基于均值和方差的局部增强：利用像素邻域内像素灰度的均值和方差。增强图像中灰度比较大但方差比较小的区域，或者使用特定的增强变换。

第三章 空域图像增强⚓